Lecture
A function ( mapping , operator , transformation ) is a mathematical concept that reflects the relationship between the elements of a set. In other words, a function is a rule according to which each element of one set (called the definition domain) is associated with some element of another set (called a range of values).
The mathematical concept of a function expresses an intuitive idea of how one quantity completely determines the value of another quantity. So the value of the variable 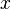 uniquely determines the value of an expression
uniquely determines the value of an expression 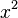 , and the value of the month uniquely determines the value of the month following it. Similarly, some pre-designed algorithm for variable input data produces certain output data.
, and the value of the month uniquely determines the value of the month following it. Similarly, some pre-designed algorithm for variable input data produces certain output data.
Often, the term “function” refers to a numeric function; that is, a function that puts some numbers in line with others. These functions are conveniently represented in the figures as graphs.
The term "function" (in a somewhat narrower sense) was first used by Leibniz (1692). In turn, Johann Bernoulli in a letter to the same Leibniz used this term in a sense that is closer to the modern one [1] .
Initially, the concept of function was indistinguishable from the concept of analytical representation. Subsequently, the definition of a function, given by Euler (1751), then - in Lacroix (1806) - was already practically in its present form. Finally, the general definition of a function (in modern form, but for numerical functions) was given by Lobachevsky (1834) and Dirichlet (1837) [2] .
By the end of the 19th century, the concept of function had grown beyond the framework of numerical systems. The vector functions were the first to do this; Frege soon introduced logical functions (1879), and after the appearance of the theory of the Dedekind sets (1887) and Peano (1911), they formulated a modern universal definition.
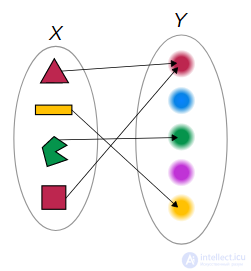
The function that associates each of the four figures with its color.
The most rigorous definition of a function is the set-theoretic definition (based on the concept of a binary relation). Often, instead of defining a function, its intuitive description is given; that is, the concept of a function is translated into ordinary language using the words “law”, “rule” or “conformity”.
Function  ( mapping , operation , operator ) is a law or a rule according to which each [3] element
( mapping , operation , operator ) is a law or a rule according to which each [3] element 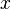 from the set
from the set 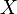 the only element mapped
the only element mapped 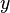 from the set
from the set 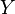 [4] .
[4] .
At the same time they say that the function  set on set
set on set 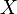 or what
or what  displays
displays 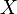 at
at 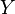 .
.
If the item 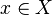 matched item
matched item 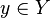 then say item
then say item 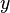 is in functional dependence
is in functional dependence  from item
from item 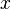 . In this case, the variable
. In this case, the variable 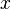 is called a function argument
is called a function argument  independent variable set
independent variable set 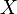 is called the scope of the task or scope of the function, and the element
is called the scope of the task or scope of the function, and the element 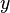 corresponding to a specific element
corresponding to a specific element 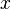 - private value of the function
- private value of the function  at the point
at the point 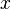 . Lots of
. Lots of 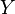 all possible particular values of the function
all possible particular values of the function  called its domain of values or region of change .
called its domain of values or region of change .
Function 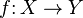 there are many ordered pairs
there are many ordered pairs 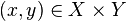 ), which satisfies the following condition: for any [3]
), which satisfies the following condition: for any [3] 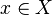 there is only one element
there is only one element 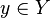 such that
such that 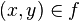 .
.
Thus, a function is an ordered triple (or tuple) of objects. 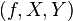 where
where
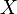 called the scope of the definition ;
called the scope of the definition ;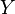 called the field of values ;
called the field of values ;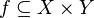 or, equivalently, a function graph.
or, equivalently, a function graph.If the function is set  which is defined on the set
which is defined on the set 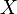 and takes values in the set
and takes values in the set 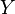 that is, the function
that is, the function  displays a lot
displays a lot 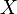 at
at 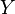 then
then
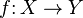 or
or 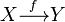 .
. (lots of
(lots of 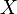 ) is denoted by
) is denoted by 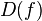 , or
, or 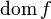 ;
; (lots of
(lots of  ) is denoted by
) is denoted by 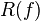 (
( 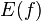 ), or
), or 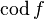 (
( 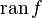 ).
).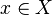 and element
and element 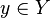 most commonly referred to as
most commonly referred to as
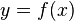 ,
,
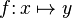 or
or
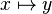 ;
;
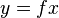 ,
, 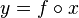 or
or 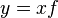 ,
,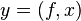 or
or 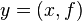 ;
;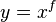 which can be found in general algebra.
which can be found in general algebra.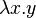 in the lambda calculus of Church.
in the lambda calculus of Church.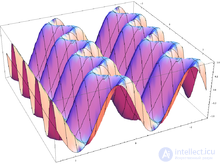
Graph of two variables function: 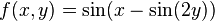
The definition of a function is easy to generalize to the case of a function of many arguments.
If many 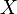 is a cartesian product of sets
is a cartesian product of sets 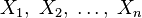 then mapping
then mapping 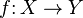 it turns out
it turns out 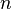 - local display, with the elements of an ordered set
- local display, with the elements of an ordered set 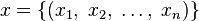 are called arguments (given
are called arguments (given 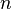 - local function), each of which runs its own set:
- local function), each of which runs its own set:
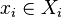 Where
Where 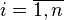 .
.
In this case 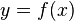 means that
means that 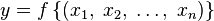 .
.
A function as a mathematical object is a binary relation satisfying certain conditions . The function can be specified directly as a set of ordered pairs, for example: 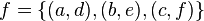 there is a function
there is a function 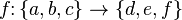 . However, this method is completely unsuitable for functions on infinite sets (which are the usual real functions: power, linear, exponential, logarithmic, etc.).
. However, this method is completely unsuitable for functions on infinite sets (which are the usual real functions: power, linear, exponential, logarithmic, etc.).
To set the function use the expression: 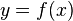 . Wherein,
. Wherein, 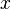 there is a variable running through the function definition domain, and
there is a variable running through the function definition domain, and 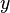 - range of values. This entry indicates the presence of a functional relationship between the elements of the sets. x and y can run through any sets of objects of any nature. These can be numbers, vectors, matrices, apples, colors of the rainbow. Let us explain by example:
- range of values. This entry indicates the presence of a functional relationship between the elements of the sets. x and y can run through any sets of objects of any nature. These can be numbers, vectors, matrices, apples, colors of the rainbow. Let us explain by example:
Let there be many 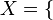 apple, plane, pear, chair
apple, plane, pear, chair 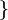 and many
and many 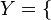 man, locomotive, square
man, locomotive, square 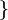 . Set the function f as follows:
. Set the function f as follows: 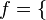 (apple, man), (plane, locomotive), (pear, square), (chair, man)
(apple, man), (plane, locomotive), (pear, square), (chair, man) 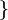 . If we introduce the variable x, the running set
. If we introduce the variable x, the running set 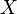 and the variable y running through the set
and the variable y running through the set 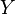 The specified function can be defined analytically, like:
The specified function can be defined analytically, like: 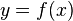 .
.
Similarly, you can set numeric functions. For example: 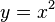 where x runs through the set of real numbers, sets some function f. It is important to understand that the expression itself
where x runs through the set of real numbers, sets some function f. It is important to understand that the expression itself 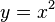 not a function. The function, as an object, is a set (ordered pairs). And this expression, as an object, is the equality of two variables. It sets the function, but is not.
not a function. The function, as an object, is a set (ordered pairs). And this expression, as an object, is the equality of two variables. It sets the function, but is not.
However, in many branches of mathematics, it is possible to denote by f (x) both the function itself and the analytical expression defining it. This syntax is extremely convenient and justified.
Numeric functions can also be specified using a graph. Let be 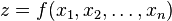 - real function of n variables.
- real function of n variables.
Consider some (n + 1) -dimensional linear space over the field of real numbers (since the function is real). Choose in this space any basis ( 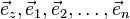 ). To each point of the function we associate a vector:
). To each point of the function we associate a vector: 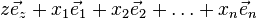 . Thus, we will have a set of vectors of linear space corresponding to points of this function according to the indicated rule. The points of the corresponding affine space will form some surface.
. Thus, we will have a set of vectors of linear space corresponding to points of this function according to the indicated rule. The points of the corresponding affine space will form some surface.
If the Euclidean space of free geometric vectors (of directed segments) is taken as the linear space, and the number of arguments of the function f does not exceed 2, the specified set of points can be visualized as a drawing (graphic). If, moreover, the original basis is taken orthonormal, we obtain the “school” definition of the graph of a function.
For functions of 3 arguments and more, such a representation is not applicable due to the lack of geometrical intuition of multidimensional spaces in a person.
However, even for such functions, you can come up with a vivid semigeometric representation (for example, for each value of the fourth coordinate of a point, to associate a certain color on the graph).
Main article: Narrowing and continuing a function
Let the mapping be given 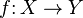 and
and 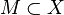 .
.
Display 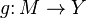 which takes on
which takes on 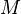 same values as function
same values as function  , is called the judgment (or otherwise limitation ) of the function
, is called the judgment (or otherwise limitation ) of the function  on the set
on the set 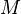 .
.
Function narrowing  on the set
on the set 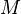 denoted by
denoted by 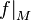 .
.
If the function 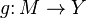 such that it is a contraction for some function
such that it is a contraction for some function 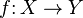 then function
then function  in turn, is called the continuation of the function
in turn, is called the continuation of the function 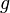 on the set
on the set 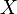 .
.
Element 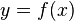 which is mapped to an element
which is mapped to an element 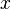 called the image of the element (point)
called the image of the element (point) 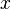 (when displaying
(when displaying  ).
).
If we take the whole subset 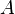 function definition areas
function definition areas  then we can consider the set of images of all elements of the set
then we can consider the set of images of all elements of the set 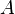 , namely a subset of the range of values (functions
, namely a subset of the range of values (functions  ) view
) view
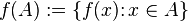 ,
,
which is called the image set 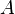 (when displaying
(when displaying  ). This set is sometimes referred to as
). This set is sometimes referred to as 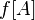 or
or 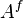 .
.
On the contrary, taking some subset 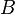 function domain
function domain  , we can consider the totality of those elements of the domain
, we can consider the totality of those elements of the domain  ), whose images fall into the set
), whose images fall into the set 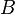 , namely - many species
, namely - many species
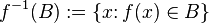 ,
,
which is called the ( complete ) prototype of the set 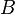 (when displaying
(when displaying  ).
).
In the particular case when many 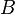 consists of one element let's say
consists of one element let's say  , lots of
, lots of 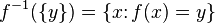 has a simpler designation
has a simpler designation 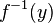 .
.
Mappings that have a domain of definition and a domain of values are called mappings of a given set into itself or transformations .
In particular, the conversion 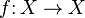 which matches each point
which matches each point 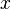 sets
sets 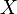 her or herself, which is the same
her or herself, which is the same
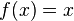 for each
for each 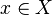 ,
,
called the identity .
This mapping has a special designation: 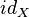 or simpler
or simpler 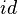 (if it is clear from the context, what set is meant). Such a designation is due to the English. the word identity ("identity, identity").
(if it is clear from the context, what set is meant). Such a designation is due to the English. the word identity ("identity, identity").
Another designation of the identity transformation is 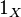 . Such a mapping is a unary operation defined on the set
. Such a mapping is a unary operation defined on the set 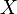 . Therefore, often, the identity transformation is called the unit transformation.
. Therefore, often, the identity transformation is called the unit transformation.
Main article: Feature Composition
Let be 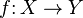 and
and 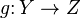 - two specified mappings such that the range of values of the first map is a subset of the range of definition of the second map. Then for everyone
- two specified mappings such that the range of values of the first map is a subset of the range of definition of the second map. Then for everyone 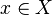 uniquely identified element
uniquely identified element 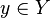 such that
such that 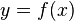 but for this very
but for this very 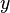 uniquely identified element
uniquely identified element 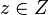 such that
such that  . That is, for everyone
. That is, for everyone 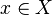 uniquely identified element
uniquely identified element 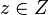 such that
such that 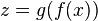 . In other words, the mapping is defined
. In other words, the mapping is defined 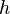 such that
such that
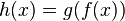 for all
for all 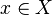 .
.
This mapping is called a mapping composition .  and
and 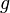 and is denoted by
and is denoted by
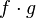 or
or 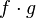 ,
,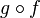 (in that order!) that is most commonly used.
(in that order!) that is most commonly used.Main article: Reverse function
If the mapping 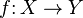 is one-to-one or bijective (see below), then the mapping is defined
is one-to-one or bijective (see below), then the mapping is defined 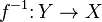 , which one
, which one
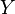 ) coincides with the display value area
) coincides with the display value area  ;
;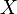 ) is the same as the display definition
) is the same as the display definition ;
;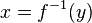 then and only if
then and only if 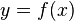 .
.This mapping is called the reverse of the mapping. .
.
A mapping for which the inverse is defined is called reversible .
In terms of the composition of a function, the property of reversibility consists in the simultaneous fulfillment of two conditions: 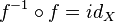 and
and 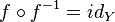 .
.
Let function be given 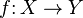 where
where 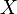 and
and 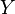 - data sets, and
- data sets, and 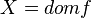 . Each such function may have some properties, which are described below.
. Each such function may have some properties, which are described below.
Image capture
Set 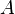 and
and 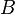 are subsets of the domain of definition. Taking an image (or, equivalently, using an operator
are subsets of the domain of definition. Taking an image (or, equivalently, using an operator  ) has the following properties:
) has the following properties:
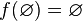 ;
;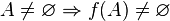 ;
;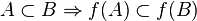 .
.Further
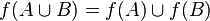 ;
;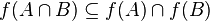 .
.The last two properties, generally speaking, admit a generalization to any number of sets greater than two (as it is formulated here).
Taking a type
Set 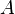 and
and 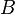 - subsets of the set
- subsets of the set 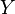 .
.
By analogy with taking an image, taking a type (transition to a type) also has the following two obvious properties:
 ;
;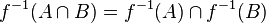 .
.These properties also allow generalization to any number of sets greater than two (as it is formulated here).
В случае, если отображение обратимо (см. ниже), прообраз каждой точки области значений одноточечный, поэтому для обратимых отображений выполняется следующее усиленное свойство для пересечений:
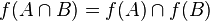 .
.Сюръективность
Основная статья: Сюръекция
Function  называется сюръективной (или, коротко, сюръекция ), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция
называется сюръективной (или, коротко, сюръекция ), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция  сюръективна , если образ множества
сюръективна , если образ множества 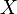 при отображении совпадает с множеством
при отображении совпадает с множеством 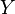 :
: 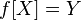 .
.
Такое отображение называется ещё отображением на .
If the surjectivity condition is violated, then such a mapping is called a mapping in .
Injectivity
Main article: Injection (mathematics)
Function  is called injective (or, briefly, injection ) if different elements of the set are
is called injective (or, briefly, injection ) if different elements of the set are 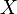 associated with different elements of the set
associated with different elements of the set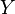 .More formally, the function is
.More formally, the function is  injective , if for any two elements
injective , if for any two elements 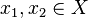 such that it
such that it 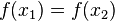 is necessarily executed
is necessarily executed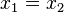 .
.
In other words, a surjection is when “every image has a type”, and an injection is when “different - into different”. That is, the injection does not happen so that two or more different elements are 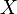 displayed in the same element
displayed in the same element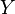 .And with a surjection, it does not happen that some element
.And with a surjection, it does not happen that some element 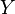 has no type.
has no type.
Bijectivity
Main article: Bijection
If the function is both surjective and injective , then such a function is called bijective or one-to-one .
Increase and decrease
Main article: Monotonic function
Let function be given 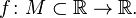 Then
Then
 is called increasing on
is called increasing on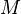 , if a
, if a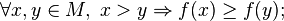
 is called increasing on
is called increasing on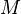 , if a
, if a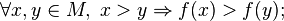
 is called decreasing by
is called decreasing by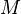 , if a
, if a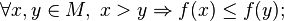
 is strictly decreasing on
is strictly decreasing on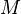 , if a
, if a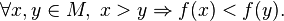
The (strictly) increasing or decreasing function is called (strictly) monotone.
Periodicity
Main article: Periodic function
Function 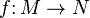 called periodic with period
called periodic with period 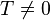 if true
if true
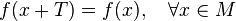 .
.
If this equality is not fulfilled for any 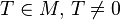 , then the function
, then the function  is called aperiodic .
is called aperiodic .
Parity
Main article: Odd and even functions
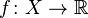 called odd if equality holds
called odd if equality holds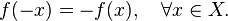
 is called even if equality is true
is called even if equality is true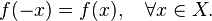
Extremum functions
Main article: Extremum
Let function be given  and
and  - internal point of the domain
- internal point of the domain 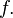 Then
Then
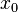 is called a point of absolute (global) maximum, if
is called a point of absolute (global) maximum, if
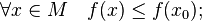
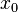 called the point of absolute minimum if
called the point of absolute minimum if
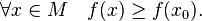
В зависимости от того, какова природа области определения и области значений, различают случаи, когда эти области — это:
В первом случае рассматриваются отображения в самом общем виде и решаются наиболее общие вопросы. Таким общим вопросом, например, является вопрос о сравнении множеств по мощности: если между двумя множествами существует взаимно однозначное отображение (биекция), то два данных множества называют эквивалентными или равномощными . Это позволяет провести классификацию множеств в виде единой шкалы, начальный фрагмент выглядит следующим образом:
Accordingly, it makes sense to consider the following mapping examples:
Во втором случае, основной объект рассмотрения — заданная на множестве структура и то, что происходит с этой структурой при отображении: если существует взаимно однозначное отображение одной структуры в другую, что при отображении сохраняются свойства заданной структуры, то говорят, что между двумя структурами установлен изоморфизм. Таким образом, изоморфные структуры, заданные в различных множествах, невозможно различить, поэтому в математике принято говорить, что данная структура рассматривается «с точностью до изоморфизма».
Существует великое разнообразие структур, которые могут быть заданы на множествах. Сюда относится:
Природа множеств определяет и свойства соответствующих функций, поскольку эти свойства формулируются в терминах структур, заданных на множествах. Например, свойство непрерывности требует задания топологической структуры .
Основная статья: Обобщённая функция
A partially defined function  from set
from set 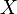 to set
to set 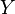 is a function
is a function 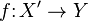 with a domain.
with a domain.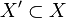 .
.
Some authors understand the function as a partially defined function. This has its advantages, for example recording is possible.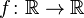 where
where 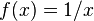 in this case
in this case 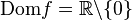 .
.
Main article: Multivalued function
By virtue of the function definition, the specified value of the argument corresponds to exactly one value of the function. Despite this, one can often hear about so-called "multi-valued" functions. In fact, this is nothing more than a convenient designation of a function, the range of values of which is itself a family of sets.
Let be 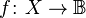 where
where 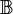 - family of subsets of a set
- family of subsets of a set 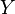 . Then
. Then 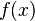 will be set for everyone
will be set for everyone 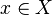 .
.
A function is unique if each value of the argument corresponds to a single value of the function. A function is multivalued if at least one value of the argument corresponds to two or more values of the function [5] .
Comments
To leave a comment
introduction to math. the basics
Terms: introduction to math. the basics