Lecture
Number is the basic concept of mathematics [1] , used for the quantitative characterization, comparison, numbering of objects and their parts. The letters used to denote numbers are numbers, as well as symbols of mathematical operations. Having emerged from the needs of the account in primitive society, the concept of number with the development of science has expanded considerably.
Natural numbers obtained by a natural account; the set of natural numbers is denoted by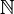 
. I.e 
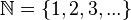(sometimes to the set of natural numbers also include zero, that is, 
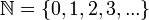). Natural numbers are closed with respect to addition and multiplication (but not subtraction or division). Addition and multiplication of natural numbers are commutative and associative, and multiplication of natural numbers is distributive with respect to addition and subtraction.
An important subset of natural numbers are prime numbers. 
A prime number is a natural number that has exactly two different natural dividers: a unit and itself. All other natural numbers, except one, are called composite. A series of prime numbers begins like this: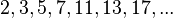 
[2] Any natural number greater than one can be represented as a product of powers of primes, with the only way up to the order of the factors. For example, 121968 = 2 4 · 3 2 · 7 · 11 2 .
Integers obtained by combining positive integers with a set of negative numbers and zero are denoted by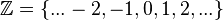 
. Integers are closed with respect to addition, subtraction and multiplication (but not division).
Rational numbers are numbers that can be represented as a fraction m / n (n 0), where m is an integer and n is a positive integer. Rational numbers are closed already relative to all four arithmetic actions: addition, subtraction, multiplication and division (except division by zero). To designate rational numbers, use the sign 
(from the English. quotient ).
Real (real) numbers are an extension of the set of rational numbers, closed with respect to some (important for mathematical analysis) transition limit operations. The set of real numbers is denoted by 
. It can be considered as the completion of the field of rational numbers. with the help of the norm, which is the usual absolute value. In addition to rational numbers, 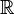includes a lot of irrational numbers 
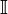not representable as a relation of the whole.
Complex numbers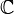 
that are an extension of the set of real numbers. They can be written as 
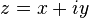where i - m. imaginary unit for which equality holds 
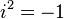. Complex numbers are used in solving problems of electrical engineering, hydrodynamics, cartography, quantum mechanics, collation theory, chaos theory, elasticity theory, and many others. Complex numbers are divided into algebraic and transcendental. Moreover, every real transcendental is irrational, and every rational number is real algebraic. More general (but still countable) classes of numbers than algebraic are periods, computable and arithmetic numbers (where each subsequent class is wider than the previous one).
For the listed sets of numbers, the following expression is true: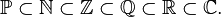 
|
|||||||||||||||||||
 |
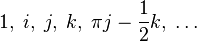Quaternions | ||||||||||||||||||
Quaternions are a kind of hypercomplex numbers. The set of quaternions is denoted by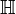 
. Quaternions, unlike complex numbers, are not commutative with respect to multiplication.
In turn the octaves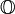 
, being an extension of quaternions, already lose the property of associativity.
Unlike octaves, sedenions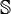 
do not have the property of alternativeness, but retain the property of power associativity.
For these sets of generalized numbers, the following expression is true: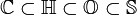 
p-adic numbers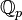 
can be considered as elements of the field, which is the completion of the field of rational numbers 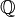with the help of so-called. p-adic valuation, similar to the field of real numbers 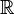defined as its replenishment using the usual absolute value.
Adeles are defined as infinite sequences {a ∞ , a 2 , a 3 , ... a p ...} , where a ∞ is any real number, and a p is p-adic, and all a p , except perhaps a finite number are integer p-adic. Adeles are added and multiplied componentwise and form a ring. The field of rational numbers is embedded in this ring in the usual way r → {r, r, ... r, ...} . The reversible elements of this ring form a group and are called ideals .
A practically important generalization of a numerical system is interval arithmetic.
for details, see Direct code, Additional code (number representation), Floating point number
To represent a natural number in the computer's memory, it is usually transferred to the binary number system. For the representation of negative numbers, an additional code of a number is often used, which is obtained by adding one to the inverted representation of the modulus of a given negative number in the binary number system.
The representation of numbers in computer memory has limitations due to the limited amount of memory allocated for numbers. Even natural numbers are a mathematical idealization, the series of natural numbers is infinite. Physical limitations are imposed on the amount of computer memory. In this connection, in a computer we are dealing not with numbers in a mathematical sense, but with some of their representations, or approximations. A certain number of cells (usually binary, bits - from BInary digiT) memory is allocated for representing numbers. If as a result of the operation, the resulting number should take more digits than is allocated to the computer, the so-called overflow occurs, and an error should be fixed. Real numbers are usually represented as floating point numbers. However, only some of the real numbers can be represented in the computer's memory by the exact value, while the remaining numbers are represented by approximate values. In the most common format, a floating-point number is represented as a sequence of bits, some of which encode the mantissa of the number, another part is the exponent, and another bit is used to indicate the sign of the number.
The concept of number arose in ancient times from the practical needs of people and developed in the process of human development. The field of human activity expanded and, accordingly, the need for quantitative description and research increased. At first, the concept of number was determined by the needs of the account and measurement, which arose in practical human activity, becoming more and more complicated. Later, the number becomes the basic concept of mathematics, and the needs of this science determine the further development of this concept.
A person was able to count objects even in ancient times, then the concept of a natural number arose. At the first stages of development, the concept of an abstract number was absent. At that time, a person could estimate the number of homogeneous objects, called one word, for example, "three people", "three axes". At the same time, different words “one”, “two”, “three” were used for the concepts “one person”, “two people”, “three people” and “one ax”, “two axes”, “three axes”. It shows an analysis of the languages of primitive peoples. Such named number series were very short and ended with the non-individualized concept of "many." Different words for a large number of objects of various kinds still exist, such as “crowd”, “herd”, “heap”. The primitive account of objects consisted in “comparing the objects of this particular aggregate with the objects of a certain definite aggregate, which plays, as it were, the role of the standard” [3] , which most of the peoples had fingers (“finger counting”). This is confirmed by the linguistic analysis of the names of the first numbers. At this stage, the concept of number becomes independent of the quality of the counted objects.
The ability to play numbers has increased significantly with the advent of writing. At first, the numbers were marked with lines on the material used for recording, for example, papyrus, clay tablets, later other signs began to be used for large numbers, as clearly shown by the Babylonian cuneiform notation and the Roman numerals preserved to our day. When in India there was a positional number system, which allows you to record any natural number with ten characters (numbers), it was a great achievement of man.
Awareness of the infinity of the natural series was the next important step in the development of the concept of a natural number. There are references to this in the writings of Euclid and Archimedes and other monuments of ancient mathematics from the 3rd century BC. er In The Beginning, Euclid establishes the unlimited continuity of a series of primes. Here, Euclid defines a number as “a set composed of units” [4] . Archimedes in the book "Psammit" describes principles for designating arbitrarily large numbers.
Over time, actions on numbers begin to be applied, first addition and subtraction, later multiplication and division. As a result of long-term development, an idea has arisen about the abstract nature of these actions, about the independence of the quantitative result of an action from the objects in question, that, for example, two objects and three objects make up five objects regardless of the nature of these objects. When they began to develop rules of action, study their properties and create methods for solving problems, then arithmetic, the science of numbers, begins to develop. The need to study the properties of numbers as such is manifested in the very process of arithmetic development, complex patterns and their interrelationships arising from the presence of actions become clear, classes of even and odd numbers, prime and composite numbers, and so on are distinguished. Then there is a branch of mathematics, which is now called number theory. When it was noted that natural numbers can characterize not only the number of objects, but also can characterize the order of objects arranged in a row, the notion of an ordinal number arises. The question of substantiating the concept of a natural number, so familiar and simple, has not been posed for a long time in science. Only by the middle of the 19th century, under the influence of the development of mathematical analysis and the axiomatic method in mathematics, there was a need to substantiate the concept of a quantitative natural number. Introduction to the use of fractional numbers was caused by the need to make measurements and became historically the first extension of the concept of number.
In the Middle Ages, negative numbers were introduced, through which it became easier to account for debt or loss. The need to introduce negative numbers was associated with the development of algebra as a science, which provides general methods for solving arithmetic problems, regardless of their specific content and initial numerical data. The need to introduce a negative number into algebra arises already when solving problems that reduce to linear equations with one unknown. Negative numbers were systematically used in solving problems as early as the 6th – 11th centuries in India and were interpreted in much the same way as it is done now.
After Descartes developed an analytical geometry that allowed him to view the roots of the equation as the coordinates of the points of intersection of a curve with the x-axis, which finally erased the fundamental difference between the positive and negative roots of the equation, negative numbers were finally used in European science.
Even in ancient Greece, a fundamentally important discovery was made in geometry: not all precisely defined segments are commensurate, in other words, not every segment can be expressed in a rational number, for example, the side of a square and its diagonal. The Euclidean Principles set forth a theory of the relationship of segments, taking into account the possibility of their incommensurability. In ancient Greece, they were able to compare such relations in magnitude, to produce arithmetic operations on them in a geometric form. Although the Greeks dealt with such relationships as with numbers, they did not realize that the ratio of the lengths of incommensurable segments could be considered as a number. This was done during the birth of modern mathematics in the 17th century when developing methods for studying continuous processes and methods for approximate calculations. I. Newton in "Universal Arithmetic" gives the definition of the concept of a real number: "By number we mean not so much the set of units, as the abstract relation of some quantity to another value of the same kind, which we have taken as one." Later, in the 70s of the 19th century, the concept of a real number was clarified on the basis of the analysis of the concept of continuity by R. Dedekind, G. Kantor and C. Weierstrass.
With the development of algebra, it became necessary to introduce complex numbers, although the distrust of the pattern of their use persisted for a long time and was reflected in the term “imaginary” that has been preserved. Already the Italian mathematicians of the 16th century (J. Cardano, R. Bombelli), in connection with the discovery of the algebraic solution of equations of the third and fourth degrees, had the idea of a complex number. The fact is that even solving a quadratic equation, if the equation does not have real roots, leads to the action of extracting a square root from a negative number. It seemed that the problem leading to the solution of such a quadratic equation has no solution. With the discovery of an algebraic solution of equations of the third degree, it turned out that in the case when all three roots of the equation are real, in the course of the calculation it is necessary to perform the action of extracting the square root of negative numbers. After establishing at the end of the 18th century a geometric interpretation of complex numbers as points on a plane and establishing the undoubted benefit of introducing complex numbers into the theory of algebraic equations, especially after the famous works of L. Euler and K. Gauss, complex numbers were recognized by mathematicians and began to play significant a role not only in algebra, but also in mathematical analysis. The value of complex numbers especially increased in the 19th century in connection with the development of the theory of functions of a complex variable. [3]
Philosophical understanding of the number laid the Pythagoreans. Aristotle testifies that the Pythagoreans considered numbers to be the “cause and beginning” of things, and relations of numbers the basis of all relations in the world. Numbers give orderliness to the world and make it a cosmos. This attitude to the number was taken by Plato, and later by the Neo-Platonists. With the help of numbers, Plato distinguishes between genuine being (that which exists and is thought of by itself), and non-genuine being, (that which exists only thanks to the other and is known only in relation). The middle position between them takes a number. It gives measure and certainty to things and makes them involved in being. Due to the number of things can be recalculated and therefore they can be conceivable, and not just perceived.Neo-Platonists, especially Iamblich and Proclus, revered the numbers so high that they did not even consider them to be real - the dispensation of the world proceeds from the number, although not directly. Numbers are super-powerful, above Mind, and inaccessible to knowledge. Neo-Platonists distinguish between divine numbers (the direct emanation of the One) and mathematical numbers (made up of ones). The latter are the imperfect likeness of the first. Aristotle, on the contrary, cites a number of arguments showing that the statement about the independent existence of numbers leads to absurdities. Arithmetic distinguishes only one aspect in these really real things and considers them in terms of their number. Numbers and their properties are the result of such consideration. Kant believed that the phenomenon is known when it is designed in accordance with a priori concepts - the formal conditions of experience.The number is one of these conditions. The number specifies a specific principle or design pattern. Any object is quantifiable and measurable, because it is constructed according to the scheme of number (or quantity). Therefore, any phenomenon can be considered mathematics. The mind perceives the nature of the subordinate numerical laws precisely because he himself builds it in accordance with the numerical laws. This explains the possibility of applying mathematics in the study of nature. Mathematical definitions developed in the 19th century were seriously revised in the early 20th century. This was caused not so much by mathematical as philosophical problems. The definitions that were given by Peano, Dedekind, or Cantor, and which are used in mathematics and nowadays, had to be substantiated by fundamental principles rooted in the very nature of knowledge.There are three such philosophical and mathematical approaches: logicism, intuitionism and formalism. The philosophical base of logicism was developed by Russell. He believed that the truth of mathematical axioms is not obvious. Truth is found by reducing to the simplest facts. A reflection of such facts Russell considered the axioms of logic, which he put in the basis of determining the number. His most important concept is the concept of class. The natural number η is the class of all classes containing η elements. Fraction is no longer a class, but a class relationship. Intuicist Brower had the opposite point of view: he considered logic only as an abstraction from mathematics, considered the natural series of numbers as basic intuition underlying all mental activity. Hilbert, the main representative of the formal school,I saw the rationale for mathematics in the construction of a consistent axiomatic base within which any mathematical concept could be formally substantiated. In the axiomatic theory of real numbers developed by him, the idea of a number is deprived of any depth and is reduced only to a graphic symbol that is substituted according to certain rules in the formulas of the theory. [four]
Comments
To leave a comment
introduction to math. the basics
Terms: introduction to math. the basics