Lecture
| 0 | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | |
| 0 | • | × | × | × | × | × | × | × | × | × |
| one | × | • | × | × | × | × | × | × | × | × |
| 2 | × | × | • | × | × | × | × | × | × | × |
| 3 | × | × | × | • | × | × | × | × | × | × |
| four | × | × | × | × | • | × | × | × | × | × |
| five | × | × | × | × | × | • | × | × | × | × |
| 6 | × | × | × | × | × | × | • | × | × | × |
| 7 | × | × | × | × | × | × | × | • | × | × |
| eight | × | × | × | × | × | × | × | × | • | × |
| 9 | × | × | × | × | × | × | × | × | × | • |
| Equality of decimal digits as a binary relation: • true, × false | ||||||||||
Equality (equality relation) in mathematics is a binary relation, the most logically strong kind of equivalence relation.
Equality is an intuitively obvious relationship: the meaning of two expressions is the same . When it is formally defined, there is inconsistency.
Set theory, by definition, considers two objects (that is, two sets ) to be equal if they consist of the same elements:
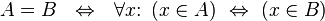
In theories with object typing, the equality relation makes sense only between elements of the same type (to put it simply, within a certain set). Logicists (first in Frege’s predicate logic, then in the framework of the theory of types) relied on a definition of equality, similar to set-theoretic, but considering relations from the other side:
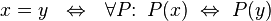
That is, for the equality of two objects, it is necessary and sufficient that any predicate that can be built on this type gives the same logical value to them. However, it was not the Logicists who invented this definition - it was also known by Leibniz.
Some formal theories shy away from the definition of equality, considering it to be initially given by an equivalence relation.
 | This section is not complete. You will help the project by correcting and adding it. |
The formal definition and intuitive understanding of equality sometimes conflicts. Is (integer) number 1 (real) number 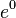 ? From the point of view of intuition, yes, and from the point of view of type theory, the question is incorrectly posed (cf. the problem of type conversion in programming). In mathematics in such cases, the canonical embedding of one set (space, type) into another is implied. The question of equality of an integer number to a real one can be understood as equality of the real number itself and another real number corresponding to our whole. That is, work with intuitively “obvious” facts like any integer is rational, and rational is real, it requires special reservations in the framework of some formal approaches.
? From the point of view of intuition, yes, and from the point of view of type theory, the question is incorrectly posed (cf. the problem of type conversion in programming). In mathematics in such cases, the canonical embedding of one set (space, type) into another is implied. The question of equality of an integer number to a real one can be understood as equality of the real number itself and another real number corresponding to our whole. That is, work with intuitively “obvious” facts like any integer is rational, and rational is real, it requires special reservations in the framework of some formal approaches.
Equation - a logical proposition constructed using equality that includes a variable. It defines a subset of the domain of a variable - the set of roots of the equation.
The definition of a value or variable is written using equality: Let the variable be equal to the expression.
Identity - statement, true for any values of variables. It is often (although not necessarily) built on the basis of the equality relation.
Comments
To leave a comment
introduction to math. the basics
Terms: introduction to math. the basics