Lecture
Euclid. Detail of the "Athenian School" by Raphael
Mathematica (ancient Greek μᾰθημᾰτικά [1] [2] . Mathematical objects are created by idealizing the properties of real or other mathematical objects and writing these properties in a formal language. Mathematics does not belong to the natural sciences, but is widely used in them both for the exact formulation of their content and for obtaining new results [3] . Mathematics is a fundamental science that provides (general) language tools to other sciences; thus, it reveals their structural interrelation and helps to find the most general laws of nature [4] .
Idealized properties of the objects under study are either formulated as axioms or are listed in the definition of the corresponding mathematical objects. Then, according to strict rules of logical inference, other true properties (theorems) are derived from these properties. This theory together forms a mathematical model of the object under study. Thus, initially, based on spatial and quantitative relations, mathematics receives more abstract relations, the study of which is also the subject of modern mathematics [5] .
Traditionally, mathematics is divided into theoretical, performing in-depth analysis of intra-mathematical structures, and applied, providing its models to other sciences and engineering disciplines, some of which occupy a position bordering on mathematics. In particular, formal logic can be considered both as part of the philosophical sciences and as part of the mathematical sciences; mechanics - and physics, and mathematics; computer science, computer technology and algorithms refer both to engineering and to the mathematical sciences, etc. Many different definitions of mathematics have been proposed in the literature.
The word "mathematics" is derived from the ancient-Greek. μάθημα, which means the study , knowledge , science , etc.-Greek. μαθηματικός, which originally means susceptible, achieves [6] , later related to the study , subsequently related to mathematics . In particular, μαθηματικὴ τέχνη, in Latin ars mathematica , means the art of mathematics . The term dr.-gk. μᾰθημᾰτικά in the modern meaning of the word “mathematics” is found already in the writings of Aristotle (4th century BC). According to Vasmer, the word came to the Russian language either through Polish. matematyka , or through the lat. mathematica [7] .
In the texts in Russian, the word “mathematics” or “mathematics” occurs at least from the 17th century, for example, in Nikolai Spafarii in the “Briefly chosen book about nine mushes and seven free arts” (1672) [8]
One of the first definitions of the subject of mathematics was given by Descartes [9] :
Only those sciences in which either order or measure is considered belong to the field of mathematics, and it is not at all essential whether these are numbers, figures, stars, sounds or anything else that this measure is sought for. Thus, there should be some general science explaining everything related to order and measure, without entering into the study of any particular subjects, and this science should be called not foreign, but the old, already entered into the name of General Mathematics.
In Soviet times, the definition from the TSB [10] given by A. N. Kolmogorov was considered classical:
Mathematics ... the science of quantitative relations and spatial forms of the real world.
This is the definition of Engels [11] ; however, further Kolmogorov explains that all the terms used should be understood in the most extended and abstract sense.
Wording Bourbaki [12] :
The essence of mathematics ... is now presented as the study of the relationship between objects, about which nothing is known, except for describing some of their properties, namely those that are the basis of the theory as axioms ... Mathematics is a set of abstract forms - mathematical structures.
Hermann Weil was pessimistic about the opportunity to give a generally accepted definition of the subject of mathematics:
The question of the foundations of mathematics and what mathematics is all about is still open. We do not know of any direction that will, in the end, find the final answer to this question, and whether it can be expected that such a “final” answer will ever be received and recognized by all mathematicians.
“Mathematization” can remain one of the manifestations of a person’s creative activity, like music-making or literary creation, vivid and original, but predicting his historical destinies cannot be rationalized and cannot be objective [13] .
1. Mathematics as an academic discipline is subdivided in the Russian Federation into elementary mathematics, studied in secondary school and educated by the disciplines:
and higher mathematics, studied in non-mathematical specialties of universities. Disciplines that are part of higher mathematics vary depending on the specialty.
The program of study in the specialty of mathematics [14] is formed by the following academic disciplines:
2. Mathematics as a specialty of scientists The Ministry of Education and Science of the Russian Federation [15] is divided into specialties:
3. For the systematization of scientific works , the section “Mathematics” [16] of the Universal Decimal Classification (UDC) is used.
4. The American Mathematical Society (AMS) has developed its own standard for the classification of sections of mathematics. It is called Mathematics Subject Classification. This standard is periodically updated. The current version is MSC 2010. The previous version is MSC 2000.
Due to the fact that mathematics works with extremely diverse and rather complex structures, the notation is also very complex. The modern system of writing formulas was formed on the basis of the European algebraic tradition, as well as mathematical analysis (the concepts of function, derivative, etc.). Geometry from time immemorial enjoyed a clear (geometric same) representation. In modern mathematics, complex graphical writing systems are also common (for example, commutative diagrams), graph-based notations are also often used.
Academician A. N. Kolmogorov proposed the following structure of the history of mathematics:
The development of mathematics began at the same time as man began to use abstractions of any high level. Simple abstraction - numbers; the understanding that two apples and two oranges, despite all their differences, have something in common, namely, they occupy both hands of one person, is a qualitative achievement of a person's thinking. In addition to the fact that the ancient people learned how to count specific objects, they also understood how to calculate abstract quantities, such as time: days, seasons, years. Arithmetic naturally began to develop from the elementary counting: addition, subtraction, multiplication and division of numbers.
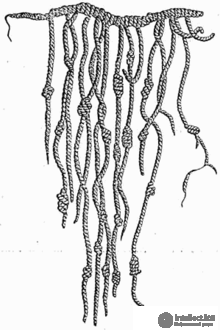
The development of mathematics is based on writing and the ability to write numbers. Probably, the ancient people first expressed the number by drawing lines on the ground or scratched them on wood. The ancient Incas, having no other writing system, represented and stored numerical data using a complex system of rope knots, the so-called pile. There were many different number systems. The first known records of numbers were found in the papyrus of Ahmes, created by the Egyptians of the Middle Kingdom. Indian civilization has developed a modern decimal number system, including the concept of zero.
Historically, the basic mathematical disciplines have emerged under the influence of the need to conduct calculations in the commercial sphere, in measuring land and to predict astronomical phenomena and, later, to solve new physical problems. Each of these spheres plays a large role in the wide development of mathematics, which consists in the study of structures, spaces and changes.
Mathematics studies imaginary, ideal objects and the relationships between them using a formal language. In the general case, mathematical concepts and theorems do not necessarily correspond to anything in the physical world. The main task of the applied section of mathematics is to create a mathematical model that is sufficiently adequate to the real object under study. The task of the mathematician-theorist is to provide a sufficient set of convenient means to achieve this goal.
The content of mathematics can be defined as a system of mathematical models and tools for their creation. The object model does not take into account all its features, but only the most necessary for the purposes of study (idealized). For example, by studying the physical properties of an orange, we can abstract away its color and taste and present it (albeit not ideally exactly) with a ball. If we need to understand how many oranges it will turn out, if we put together two and three, then we can abstract from the form, leaving the model with only one characteristic - the quantity. Abstraction and the establishment of connections between objects in the most general form is one of the main directions of mathematical creativity.
Another direction, along with abstraction - a generalization. For example, generalizing the concept of "space" to the space of n-dimensions. " Space 
at 
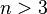is a mathematical invention. However, a very ingenious fiction that helps mathematically understand complex phenomena . ” [17]
The study of intra-mathematical objects, as a rule, occurs with the help of an axiomatic method: first, the list of basic concepts and axioms are formulated for the objects under study, and then, using the inference rules, substantial theorems are obtained from the axioms, which together form the mathematical model.
The question of the essence and foundations of mathematics has been discussed since the time of Plato. Since the 20th century, there has been comparative agreement on the question of what should be considered rigorous mathematical proof, but there is no agreement on the understanding that in mathematics it is considered initially true. This leads to disagreements both in matters of axiomatics and the interrelation of the branches of mathematics, and in the choice of logical systems, which should be used in evidence.
In addition to skepticism, the following approaches to this issue are known.
It is proposed to consider all mathematical objects in the framework of set theory, most often with the Zermelo – Fraenkel axiomatics (although there are many others equivalent to it). This approach is considered to be predominant from the middle of the 20th century; however, in reality, most mathematical works do not aim to translate their statements strictly into the language of set theory, but operate with concepts and facts established in some areas of mathematics. Thus, if a contradiction is found in set theory, it will not entail the devaluation of most of the results.
This approach assumes strict typing of mathematical objects. Many paradoxes, avoided in set theory only by special tricks, prove to be impossible in principle.
This approach involves the study of formal systems based on classical logic.
Intuitionism presupposes, at the base of mathematics, intuitionistic logic, which is more limited in the means of proof (but, as it is believed, more reliable). Intuitionism rejects proof by contradiction, many non-constructive proofs become impossible, and many problems of set theory become meaningless (non-formalizable).
Constructive mathematics is a flow in mathematics close to intuitionism, which studies constructive constructions [to clarify ] . According to the criterion of constructiveness - "to exist - it means to be built ." [18] The constructiveness criterion is a stronger requirement than the consistency criterion. [nineteen]
Pythagoras also discussed the question of whether mathematics is more art than science, or vice versa. The aesthetic perception of mathematics is based [the source is not specified 282 days ] on the assumption coming from Plato about the a priori mathematical knowledge (which is now, however, disputed). According to him, mathematical knowledge exists independently of human consciousness and “opens up” in the same way as Columbus “discovered” America. This allows you to admire the mathematical results in the same way as the pictures of Velázquez or Caravaggio, reflecting the objective surrounding reality outside of human consciousness.
The concept of "number" originally referred to natural numbers. Later it was gradually extended to whole, rational, real, complex and other numbers.
|
|||||||||||||||
 |
 |
||||||||||||||
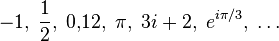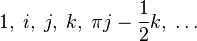| Complex numbers | Quaternions | ||||||||||||||
Numbers - Natural Numbers - Integers - Rational Numbers - Real Numbers - Complex Numbers - Hypercomplex Numbers - Quaternions - Oktonions - Sedenions - Hyperreal Numbers - Surreal Numbers - P -Adic Numbers - Mathematical Constants - Number Names - Infinity - Bases
[show]  Numerical Systems |
|---|
 |
 |
 |
 |
| Arithmetic | Differential and integral calculus | Vector analysis | Analysis |
 |
 |
 |
|
| Differential equations | Dynamic systems | Chaos theory |
Arithmetic - Vector analysis - Analysis - Measure theory - Differential equations - Dynamic systems - Chaos theory
Set theory - Linear algebra - General algebra (includes, in particular, group theory, universal algebra, category theory) - Algebraic geometry - Number theory - Topology.
 |
 |
 |
 |
 |
 |
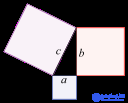
| Geometry | Trigonometry | Differential geometry | Topology | Fractals | Measure theory |
Геометрия — Тригонометрия — Алгебраическая геометрия — Топология — Дифференциальная геометрия — Алгебраическая топология — Линейная алгебра —Фракталы — Теория меры
Дискретная математика включает средства исследования объектов, способных принимать только отдельные (дискретные) значения (то есть объектов, не способных изменяться плавно). [20]
 |
 |
 |
 |
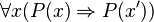| Mathematical logic | Теория вычислимости | Cryptography | Graph theory |
Комбинаторика — Теория множеств — Теория решёток — Математическая логика — Теория вычислимости— Криптография — Теория функциональных систем — Теория графов — Теория алгоритмов — Логические исчисления — Информатика
Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные. [22] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.
Популяризаторы науки
Comments
To leave a comment
introduction to math. the basics
Terms: introduction to math. the basics