Variable

Variable is an attribute of a physical or abstract system that can change its value. The value may vary depending on the context in which the system is considered, or, if specified, which system is being discussed. The concept of a variable is widely used in areas such as math, science, engineering and programming. Examples of variables include air temperature, a function parameter, and more. In a broad sense, a variable is characterized only by the set of values ​​it can take.

Variables in Math

In mathematics, a variable is a quantity characterized by a set of values ​​that it can take. ^[1] This can mean both a real physical quantity, temporarily considered in isolation from its physical context, and a certain abstract quantity that has no analogues in the real world. In mathematical analysis and most adjacent branches of mathematics, the term “variable” is usually understood as a numerical value, the set of accepted values ​​of which is included in the set of real numbers.

The set of all the values ​​that a given variable can take is called the scope of this variable. This set and sets the variable, that is, formally and is her.

In modeling, variables must be distinguished from parameters, despite the fact that a variable in one context may be a parameter in another.

In applied statistics, a variable is an evaluative factor, or a characteristic, or an individual or system attribute. In other words, something that is expected to change over time or between individuals.

Designations

• Variables are denoted by small letters of the Latin or Greek alphabet (possibly with indices): .
• Regions of change of the corresponding variables are usually denoted by the same symbols, taken in braces: .

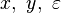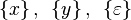It should be noted that the unknowns in equations, inequalities, and other similar problems are denoted similarly. For example, 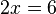. In this case, it is not the variables that are meant, although the concepts are very similar and depend on the context.

The essence of this difference between the unknown and the variable can be explained as follows. Record 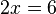on the one hand, it can be interpreted as a statement about the property of the unknown (at the moment when the statement is made) 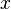, the value of which can be found (or clarified), starting from the above statement as from the initial premise. In this case 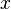will be a specific designation, but before the calculations (for example, solving the equation) of an unknown quantity . On the other hand a record 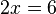can be interpreted as a predicate that takes the value of "true" for the same values ​​that are substituted in place 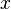, and the meaning of "false" with others. In this case 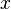is a designation of a place in the expression , on which different (variable) values ​​can be substituted in order to determine the logical (boolean) value of the written predicate. In this case 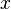it is more correct to consider as a variable .

Variables in programming

In programming, a variable is an identifier that identifies data. Usually this is a name that hides the memory area with the data stored there. A variable can have a type that characterizes the set of values ​​that it can take. In programming, variables are usually denoted by one or more words or symbols, such as "time", "x", "foo", and the like.

It should be noted that this value is somewhat similar to the mathematical one. In the 17th century, mathematicians invented a variable precisely in order to “book” a place in the formula, into which a concrete value can be substituted at the right time. The paper in this process is memory, and symbols (more often, letters) reserve and name areas of this memory. The sense of ambiguity arises from the fact that the formula in mathematics plays a dual role: if it is an algorithm for computing, the meaning coincides with the programmer's definition; if the formula visualizes the relationships of its elements, we abstract away from the role of a variable, like memory cells, such an understanding loses its meaning.

Variables in physics

In physics, a variable is a certain attribute of the model of a real physical process, which assumes quantitative values, a physical quantity. The set of values ​​that a particular variable can take is determined from physical considerations. Physical variables are associated with each other by physical laws, resulting in mathematical models of varying degrees of complexity. Variables in physics, as a rule, besides quantitative values, are also characterized by dimension.

Notes