Lecture
An operation is a mapping that associates one or more elements of a set (argument) with another element (value). The term “operation” is usually applied to arithmetic or logical actions, in contrast to the term “operator”, which is more often applied to some mappings of a set onto itself that have remarkable properties.
Operation 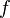 - mapping whose domain is the direct product of several sets. Mathematically, the operation can be written as
- mapping whose domain is the direct product of several sets. Mathematically, the operation can be written as 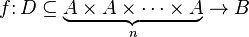 (
( 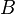 and
and 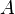 may coincide), where
may coincide), where 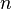 called the arity of the operation.
called the arity of the operation.
Main article: Arnost
Operations differ in the number of sets whose Cartesian product is its domain of definition. For example, an operation can be unary if it maps one element of a set to one element of a set, or binary if it matches one element of a set to two elements of a set.
An algebraic operation is an operation. 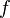 , in which
, in which 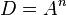 and
and 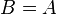 where
where 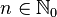 - arity, i.e.
- arity, i.e. 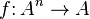 . [one]
. [one]
Operations may or may not have different properties. For example:
 "When
"When 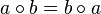 .
.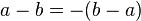 .
. "When
"When 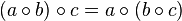 .
.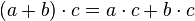 .
. "Transitive if of ratios
"Transitive if of ratios 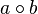 and
and 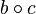 follows that
follows that 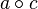 .
.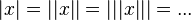 .
.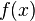 right that
right that 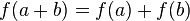 , the function is additive.
, the function is additive.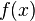 right that
right that 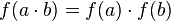 , the function is multiplicative.
, the function is multiplicative.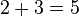 .
.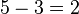 .
.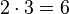 .
.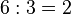 .
.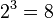 .
.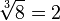 .
.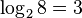 .
.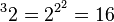 .
.Addition and negation are elementary arithmetic operations. All other, more complex operations are obtained as a result of hyperoperations. Thus, addition and subtraction are attributed to first-stage operations; multiplication and division - to the operations of the second stage; exponentiation, root extraction and logarithm — to third stage operations; Tetration and its inverse operations are rarely used operations of the fourth step, but this hyper-operation can be continued indefinitely, up to operations of the 5th, 6th and higher stages.
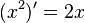 .
.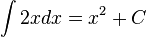 .
.Logical operations are operations on elements from a set of two elements: “true” and “false”, or “1” and “0”.
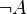 ) - unary operation; converts "1" to "0", and "0" to "1".
) - unary operation; converts "1" to "0", and "0" to "1".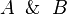 ) - binary operation; returns “1” only if both arguments are “1”.
) - binary operation; returns “1” only if both arguments are “1”.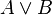 ) - binary operation; returns "0", only if both arguments are "0".
) - binary operation; returns "0", only if both arguments are "0".
Comments
To leave a comment
introduction to math. the basics
Terms: introduction to math. the basics