Lecture
Это окончание невероятной информации про основные понятия теории надежности.
...
определяющее наработку объекта до отказа, то Р(t) = P(T і t), то есть вероятность безотказной работы - это вероятность того, что время Т от момента включения объекта до его отказа будет больше или равно времени t, в течение которого определяется вероятность безотказной работы. Из вышесказанного следует, что 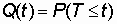 . Вероятность отказа есть функция распределения времени работы Т до отказа:
. Вероятность отказа есть функция распределения времени работы Т до отказа: 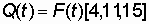 . Статистическая оценка вероятности отказа:
. Статистическая оценка вероятности отказа:
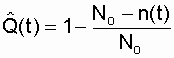 ; . (2.3)
; . (2.3)
Из [4, 13, 15] известно, что производная от вероятности отказа по времени есть плотность вероятности или дифференциальный закон распределения времени работы объекта до отказа
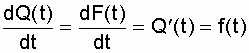 . (2.4)
. (2.4)
Полученная математическая связь позволяет записать
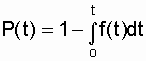 .
.
Таким образом, зная плотность вероятности ¦ (t), легко найти искомую величину P(t).
На практике достаточно часто приходится определять условную вероятность безотказной работы объекта в заданном интервале времени Р (t 1 , t 2 ) при условии, что в момент времени t 1 объект работоспособен и известны Р (t 1 ) и Р (t 2 ). На основании формулы вероятности совместного появления двух зависимых событий, определяемой произведением вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило [4, 13], запишем
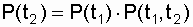 , откуда
, откуда
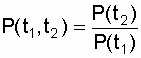 . (2.5)
. (2.5)
По известным статистическим данным можно записать:
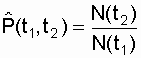 ,
,
где N (t 1 ), N (t 2 ) - число объектов, работоспособных соответственно к моментам времени t 1 и t 2 :
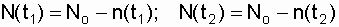 .
.
Отметим, что не всегда в качестве наработки выступает время (в часах, годах). К примеру, для оценки вероятности безотказной работы коммутационных аппаратов с большим количеством переключений (вакуумный выключатель) в качестве переменной величины наработки целесообразно брать количество циклов "включить" - "выключить". При оценке надежности скользящих контактов удобнее в качестве наработки брать количество проходов токоприемника по этому контакту, а при оценке надежности движущихся объектов наработку целесообразно брать в километрах пробега. Суть математических выражений оценки P(t), Q(t), f(t) при этом остается неизменной.
2.1.2. Средняя наработка до отказа
Средней наработкой до отказа называется математическое ожидание наработки объекта до первого отказа T 1 .
Вероятностное определение средней наработки до отказа [13] выражается так: 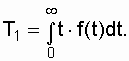
Используя известную связь между f(t), Q(t) и P(t), запишем 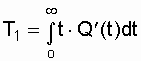 , а зная, что
, а зная, что 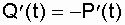 , получим:
, получим:
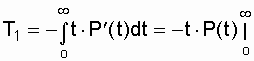 +
+ 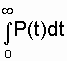 .
.
Полагая, что 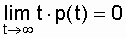 и учитывая, что Р(о) = 1, получаем:
и учитывая, что Р(о) = 1, получаем:
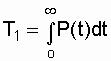 . (2.6)
. (2.6)
Таким образом, средняя наработка до отказа равна площади, образованной кривой вероятности безотказной работы P(t) и осями координат. Статистическая оценка для средней наработки до отказа определяется по формуле
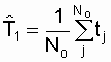 , ч. (2.7)
, ч. (2.7)
где N o - число работоспособных однотипных невосстанавливаемых объектов при
t = 0 (в начале испытания); tj - наработка до отказа j-го объекта.
Отметим, что как и в случае с определением P(t) средняя наработка до отказа может оцениваться не только в часах (годах), но и в циклах, километрах пробега и другими аргументами.
2.1.3. Интенсивность отказов
Интенсивность отказов - это условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не наступил. Из вероятностного определения следует, что
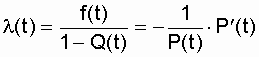 . (2.8)
. (2.8)
Статистическая оценка интенсивности отказов имеет вид :
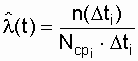 , (2.9)
, (2.9)
где 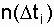 - число отказов однотипных объектов на интервале
- число отказов однотипных объектов на интервале 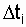 , для которого определяется
, для которого определяется 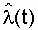 ;
; 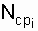 - число работоспособных объектов в середине интервала
- число работоспособных объектов в середине интервала 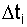 (см. рис. 2.2).
(см. рис. 2.2).
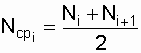 ,
,
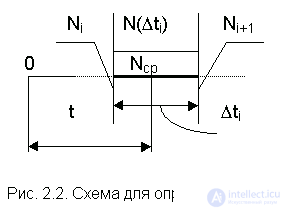
где N i - число работоспособных объектов в начале интервала 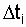 ;
;
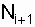 - число работоспособных объектов в конце интервала
- число работоспособных объектов в конце интервала 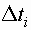 .
.
Если интервал 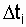 уменьшается до нулевого значения (
уменьшается до нулевого значения ( 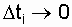 ),то
),то
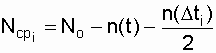 , (2.10)
, (2.10)
где N о - количество объектов, поставленных на испытания; 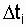 - интервал, продолжающий время t;
- интервал, продолжающий время t; 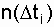 - количество отказов на интервале
- количество отказов на интервале 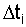 .
.
Умножив и поделив в формуле (2.10) правую часть на N о и перейдя к предельно малому значению D t, вместо выражения (2.9), получим
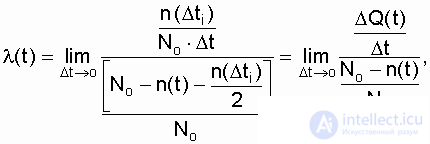
где 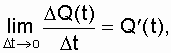 but
but 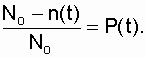
Следовательно,
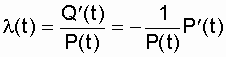 ,
,
что и записано в вероятностном определении l (t), см. выражение (2.8).
Решение [13] выражения (2.8) дает:
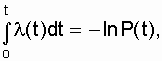 or
or 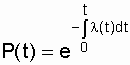 . (2.11)
. (2.11)
Выражение (2.11) показывает связь l (t) и P(t). Из этой связи ясно видно, что по аналитически заданной функции l (t) легко определить P(t) и Т 1 :
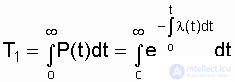 . (2.12)
. (2.12)
Если при статистической оценке 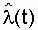 время эксперимента разбить на достаточно большое количество одинаковых интервалов D t за длительный срок, то результатом обработки опытных данных будет график, изображенный на рис. 2.3.
время эксперимента разбить на достаточно большое количество одинаковых интервалов D t за длительный срок, то результатом обработки опытных данных будет график, изображенный на рис. 2.3.
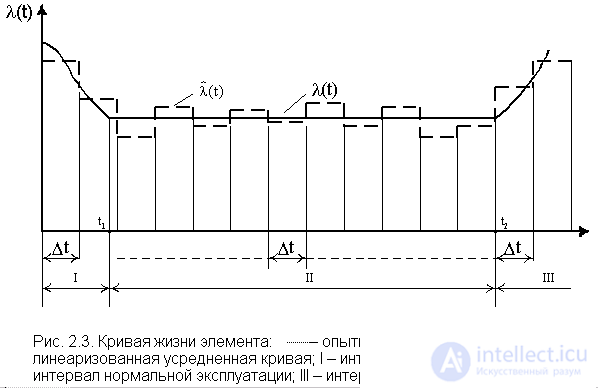
Как показывают многочисленные данные анализа надежности большинства объектов техники, в том числе и электроустановок, линеаризованная обобщенная зависимость l (t) представляет собой сложную кривую с тремя характерными интервалами (I, II, III). На интервале II (t 2 - t 1 ) l = const. Этот интервал может составлять более 10 лет [8], он связан с нормальной эксплуатацией объектов. Интервал I (t 1 - 0) часто называют периодом приработки элементов. Он может увеличиваться или уменьшаться в зависимости от уровня организации отбраковки элементов на заводе-изготовителе, где элементы с внутренними дефектами своевременно изымаются из партии выпускаемой продукции. Величина интенсивности отказов на этом интервале во многом зависит от качества сборки схем сложных устройств, соблюдения требований монтажа и т.п. Включение под нагрузку собранных схем приводит к быстрому "выжиганию" дефектных элементов и по истечении некоторого времени t 1 в схеме остаются только исправные элементы, и их эксплуатация связана с l = const. На интервале III (t > t 2 ) по причинам, обусловленным естественными процессами старения, изнашивания, коррозии и т.д., интенсивность отказов резко возрастает, увеличивается число деградационных отказов. Для того, чтобы обеспечить l = const необходимо заменить неремонтируемые элементы на исправные новые или работоспособные, отработавшие время t << t 2 . Интервал
l = const cоответствует экспоненциальной модели распределения вероятности безотказной работы. Эта модель подробно проанализирована в подразделе 3.2. Здесь же отметим, что при l = const значительно упрощается расчет надежности и l наиболее часто используется как исходный показатель надежности элемента [14, 18, 19].
2.1.4. Средняя наработка на отказ
Этот показатель относится к восстанавливаемым объектам, при эксплуатации которых допускаются многократно повторяющиеся отказы. Эксплуатация таких объектов может быть описана следующим образом: в начальный момент времени объект начинает работу и продолжает работу до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до отказа и т.д. На оси времени моменты отказов образуют поток отказов, а моменты восстановлений - поток восстановлений.
Средняя наработка на отказ объекта (наработка на отказ) определяется как отношение суммарной наработки восстанавливаемого объекта к числу отказов, происшедших за суммарную наработку:
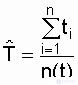 , (2.13)
, (2.13)
где t i - наработка между i-1 и i-м отказами, ч; n(t) - суммарное число отказов за время t.
2.1.5. Параметр потока отказов
Этот показатель также характеризует восстанавливаемый объект и по статистическим данным определяется с помощью формулы:
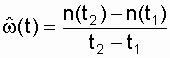 , (2.14)
, (2.14)
где n(t 1 ) и n(t 2 ) - количество отказов объекта, зафиксированных соответственно, по истечении времени t 1 и t 2 .
Если используются данные об отказах по определенному количеству восстанавливаемых объектов, то
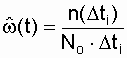 , (2.15)
, (2.15)
где 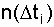 - количество отказов по всем объектам за интервал времени
- количество отказов по всем объектам за интервал времени 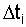 ; N о - количество однотипных объектов, участвующих в эксперименте (отказавший объект восстанавливается, N о = соnst). Нетрудно увидеть, что выражение (2.14) похоже на выражение (2.8) с той лишь разницей, что при определении
; N о - количество однотипных объектов, участвующих в эксперименте (отказавший объект восстанавливается, N о = соnst). Нетрудно увидеть, что выражение (2.14) похоже на выражение (2.8) с той лишь разницей, что при определении 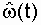 предполагается моментальное восстановление отказавшего объекта или замена отказавшего однотипным работоспособным, то есть N о = соnst.
предполагается моментальное восстановление отказавшего объекта или замена отказавшего однотипным работоспособным, то есть N о = соnst.
Параметр потока отказов представляет собой плотность вероятности возникновения отказа восстанавливаемого объекта. Отказы объектов возникают в случайные моменты времени и в течение заданного периода эксплуатации наблюдается поток отказов. Существует множество математических моделей потоков отказов. Наиболее часто при решении задач надежности электроустановок используют простейший поток отказов - пуассоновский поток [13, 15]. Простейший поток отказов удовлетворяет одновременно трем условиям: стационарности, ординарности, отсутствия последствия.
Стационарность случайного процесса (времени возникновения отказов) означает, что на любом промежутке времени 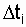 вероятность возникновения n отказов зависит только от n и величины промежутка
вероятность возникновения n отказов зависит только от n и величины промежутка 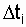 , но не зависит от сдвига
, но не зависит от сдвига 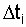 по оси времени. Следовательно, при
по оси времени. Следовательно, при 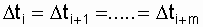 вероятность появления n отказов по всем интервалам составит
вероятность появления n отказов по всем интервалам составит
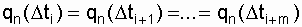 .
.
Ординарность случайного процесса означает, что отказы являются событиями случайными и независимыми. Ординарность потока означает невозможность появления в один и тот же момент времени более одного отказа, то есть 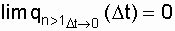 .
.
Отсутствие последствия означает, что вероятность наступления n отказов в течение промежутка 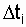 не зависит от того, сколько было отказов и как они распределялись до этого промежутка. Следовательно, факт отказа любого элемента в системе не приведет к изменению характеристик (работоспособности) других элементов системы, если даже система и отказала из-за какого-то элемента.
не зависит от того, сколько было отказов и как они распределялись до этого промежутка. Следовательно, факт отказа любого элемента в системе не приведет к изменению характеристик (работоспособности) других элементов системы, если даже система и отказала из-за какого-то элемента.
Опыт эксплуатации сложных технических систем показывает, что отказы элементов происходят мгновенно и если старение элементов отсутствует ( l = const), то поток отказов в системе можно считать простейшим.
Случайные события, образующие простейший поток, распределены по закону Пуассона [4,13, 15]:
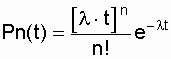 при n і 0 (2.16)
при n і 0 (2.16)
где Рn(t) - вероятность возникновения в течение времени t ровно n событий (отказов); l - параметр распределения, совпадающий с параметром потока событий.
Если в выражении (2.16) принять n = 0, то получим 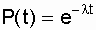 - вероятность безотказной работы объекта за время t при интенсивности отказов l = const. Нетрудно доказать, что если восстанавливаемый объект при отсутствии восстановления имеет характеристику l = const, то, придавая объекту восстанавливаемость, мы обязаны записать w (t) = const; l = w [13]. Это свойство широко используется в расчетах надежности ремонтируемых устройств. В частности, в [9, 10, 14, 18, 21] важнейшие показатели надежности оборудования электроустановок даны в предположении простейших потоков отказов и восстановлений, когда
- вероятность безотказной работы объекта за время t при интенсивности отказов l = const. Нетрудно доказать, что если восстанавливаемый объект при отсутствии восстановления имеет характеристику l = const, то, придавая объекту восстанавливаемость, мы обязаны записать w (t) = const; l = w [13]. Это свойство широко используется в расчетах надежности ремонтируемых устройств. В частности, в [9, 10, 14, 18, 21] важнейшие показатели надежности оборудования электроустановок даны в предположении простейших потоков отказов и восстановлений, когда 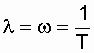 и соответственно
и соответственно 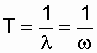 .
.
Часть 1 1. BASIC TERMS OF RELIABILITY THEORY
Часть 2 - 1. BASIC TERMS OF RELIABILITY THEORY
Comments
To leave a comment
Theory of Reliability
Terms: Theory of Reliability