Lecture
The problem of stability - plasticity in pattern recognition. The principle of adaptive resonance by Stefan Grossberg and Gail Carpenter. Neural network architecture APT.
The problem of stability-plasticity is one of the most difficult and difficult tasks in the construction of artificial systems that simulate perception. The nature of the perception of the external world by living organisms (and, above all, by man) is constantly connected with the solution of the dilemma, is whether some image is “new” information, and therefore the reaction to it must be search-and-cognitive, with this image being retained in memory, or is a version of the "old", already familiar picture, and in this case, the reaction of the organism should correspond to the previously accumulated experience. Special memorization of this image is not required in the latter case. Thus, the perception is simultaneously plastic , adapted to the new information, and at the same time it is stable , that is, it does not destroy the memory of old images.
The neural systems considered in previous lectures are not adapted to solving this problem. For example, a multilayer perceptron, trained by the method of reverse propagation, remembers the entire package of training information, while the images of the training sample are presented in the process of training many times. Attempts to train the perceptron in a new way will lead to the modification of synaptic connections with uncontrollable, generally speaking, destruction of the memory structure of previous images. Thus, the perceptron is not capable of memorizing new information, a complete retraining of the network is necessary.
A similar situation occurs in the networks of Kohonen and Lippmann-Hemming, studying on the basis of self-organization. These networks always give a positive result in the classification. Thus, these neural networks are not able to separate new images from distorted or noisy versions of old images.
Studies on the problem of stability-plasticity, performed at the Center for Adaptive Systems of Boston University under the leadership of Stefan Grossberg, led to the construction of the theory of adaptive resonance (ART) and the creation of a new type of neural network architectures based on it. We turn to the consideration of the general provisions of ART, put forward by S. Grossberg in 1976 and detailed in the foundational work of 1987 (S. Grossberg, G. Carpenter, 1987).
An attractive feature of neural networks with adaptive resonance is that they retain plasticity when memorizing new images, and, at the same time, prevent modification of the old memory. The neural network has an internal novelty detector - a test for comparing the displayed image with the contents of the memory. With a successful search in the memory, the revealed image is classified with a simultaneous specifying modification of the synaptic weights of the neuron that performed the classification. Such a situation is spoken of as the occurrence of adaptive resonance in the network in response to the presentation of the image. If the resonance does not occur within a certain predetermined threshold level, then the novelty test is considered successful, and the image is perceived by the network as new. The modification of the weights of neurons that have not experienced resonance is not performed.
An important concept in the theory of adaptive resonance is the so-called critical feature pattern of information. This term indicates that not all features (details) presented in some way are essential for the perception system. The recognition result is determined by the presence of specific critical features in the image. Consider this by example.
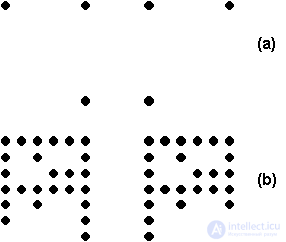
Fig. 11.1. Illustration to the concept of critical features of the image.
Both pairs of pictures in Fig. 11.1 have a common feature: in each of the pairs, the black dot in the lower right corner is replaced by white, and the white dot in the lower left corner is replaced by black. Such a change for the lower pair of pictures (in the figure - pair (b)) is obviously nothing more than noise, and both images (b) are distorted versions of the same image. Thus, the changed points are not critical for this image.
The situation is quite different for the top pair of pictures (a). Here the same change of points is too significant for the image, so that the right and left images are different images. Consequently, the same feature of the image can be insignificant in one case, and critical in the other. The task of the neural network will be to form the correct response in both cases: the "plastic" decision on the appearance of a new image for the pair (a) and the "stable" decision on the coincidence of the pictures (b). In this case, the allocation of the critical part of the information should be obtained automatically in the process of working and training the network, based on its individual experience.
Note that, in the general case, just listing the features (even if a person first performs it, assuming certain conditions for further network operation) may not be enough for the successful functioning of an artificial neural system, the specific connections between several separate features may be critical.
The second significant conclusion of the theory is the necessity of self-adhering the algorithm of image search in memory. The neural network operates in constantly changing conditions, so that a predefined search pattern that corresponds to a certain information structure may later prove to be ineffective when changing this structure. In the theory of adaptive resonance, this is achieved by introducing a specialized orienting system, which self-consistently terminates the further search for resonance in memory, and decides on the novelty of the information. The orienting system is also trained in the process.
In the case of a resonance, the theory of ART suggests the possibility of direct access to the image of memory that responded to the resonance. In this case, the pattern of critical features is the key prototype for direct access.
These and other features of the theory of adaptive resonance are reflected in neural network architectures, which received the same name - ART.
There are several varieties of ART networks. Historically, the first was the network, later called ART-1 (S.Grossberg, G.Carpenter, 1987). This network is focused on processing images containing binary information. The next step - the architecture of ART-2, published in the same 1987 (S.Grossberg, G.Carpenter, 1987) - focused on working with both binary and analog images. A relatively recent report on the ART-3 system (G. Carpenter, 1990) refers to the extension of the adaptive resonance theory of Grossberg and Carpenter to multi-layer neuroarchitecture. In our lecture, we will focus on the classic network ART-1.
The neural system ART-1 is a classifier of input binary images in several categories formed by the network. The decision is made in the form of excitation of one of the neurons of the recognition layer, depending on the degree of image similarity to the pattern of critical features of this category. If this degree of similarity is small, i.e. Since the image does not correspond to any of the existing categories, a new class will be formed for it, which will be further modified and refined by other images, forming its own pattern of critical features. To describe the new category, a new, previously unused neuron in the recognition layer is assigned.
The full description of the network structure of adaptive resonance and the theory of its work, presented in the original publication by Grossberg and Carpenter, is very cumbersome, so in our presentation we follow the later book of F. Wassermen, complementing it with a general description of the features of ART-2 and the new architecture of ART 3
The network ART-1 consists of five functional modules (Fig. 11.2): two layers of neurons - a comparison layer and a recognition layer , and three control specialized neurons - reset , control 1 and control 2 .
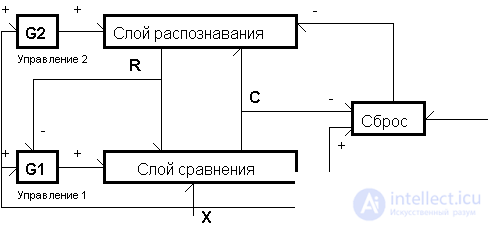
Fig. 11.2. The general scheme of the neural network ART-1.
The initial value of the control neuron 1 is assumed to be unity: G1 = 1. The input binary vector X enters the comparison layer, which initially passes it without change, while the output vector of the comparison layer is C = X. This is achieved by applying the so-called 2/3 rule for the neurons of the comparison layer. Each of the neurons of this layer has three binary inputs - a signal from the corresponding component of the vector X, a signal from the control neuron 1 and a feedback signal from the recognition layer P (which is zero at the initial time). To activate a neuron in the comparison layer, it is required that at least two of the three signals be equal to one, which is achieved at the initial moment by the input from control 1 and the active components of the X vector.
The signal C developed by the comparison layer is fed to the inputs of the neurons of the recognition layer. Each neuron of the recognition layer has a weight vector b j - real numbers, and only one neuron of this layer is excited, the weight vector of which is closest to C. This can be achieved, for example, through the mechanism of lateral inhibition "Winner takes all" (Lecture 7). The output of the winning neuron is set to unity, the remaining neurons are completely inhibited. The feedback signal from the winning neuron is fed back into the comparison layer via synaptic weights T. Vector T is essentially the carrier of the critical traits of the category determined by the winning neuron.
The output of the neuron of control 1 is equal to one, only when the input image X has nonzero components, that is, this neuron performs the function of detecting the fact of the arrival of the image at the input. However, when a non-zero response of the neurons of the recognition layer R occurs, the control value 1 is set to zero G1 = 0.
The control neuron 2 signal is also set to unity with a non-zero vector X. The task of this neuron is to cancel the activity on the recognition layer if no information has entered the network.
So, when generating the response R of the recognition layer, the output G1 = 0, and now the neurons of the comparison layer are activated by signals of the image X and the response R. The two-thirds rule leads to activation of only those neurons of the comparison layer for which both X and R are single. Thus, the output of the comparison layer C is no longer exactly equal to X, but contains only those components of X that correspond to the critical features of the winning category. This mechanism in the theory of ART has been called the adaptive filtering of image X.
Now the task of the system is to determine whether the set of these critical features is sufficient for the final assignment of the image of X to the category of the winning neuron. This function is performed by a reset neuron, which measures the similarity between the X and C vectors. The output of the reset neuron is determined by the ratio of the number of single components in vector C to the number of single components of the original image X. If this ratio is below a certain level of similarity, the neuron issues a reset signal indicating that the level of resonance of the image of X with the features of the proposed category is not sufficient for a positive conclusion about the completion of the classification. The condition for the reset signal is the ratio
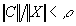 ,
,
where r <1 is the similarity parameter.
The reset signal performs a complete deceleration of the neuron-winner-loser, who does not accept further participation in the network.
Let us describe successively events occurring in the ART network in the process of classification.
The zero values of the components of the input vector X set the signal of the neuron of control 2 to zero, while simultaneously setting the outputs of the neurons of the recognition layer to zero. When non-zero values of X occur, both control signals (G1 and G2) are set to one. In this case, according to the two-thirds rule, the outputs of the neurons of the comparison layer C are exactly equal to the components of X.
The vector C is fed to the inputs of the neurons of the recognition layer, which, in competition, determine the winning neuron that describes the intended result of the classification. As a result, the output vector R of the recognition layer contains exactly one unit component, the remaining values are equal to zero. A non-zero output of the winning neuron sets the control signal 1 to zero: G1 = 0. By feedback, the winning neuron sends signals to the comparison layer, and the comparison phase begins.
In the comparison layer, the fan of the recognition layer response signals is compared with the components of the vector X. The output of the comparison layer C now contains single components only in those positions in which the input vector X and the feedback vector P also have units. If the result of comparing the vectors C and X no significant differences will be detected, then the neuron discharge is inactive. Vector C will again cause excitation of the same winner neuron in the recognition layer, which will successfully complete the classification process. Otherwise, a reset signal will be generated, which will inhibit the winning neuron in the recognition layer, and the search phase will begin.
As a result of the decelerating reset signal, all neurons of the recognition layer will receive zero outputs, and, therefore, control neuron 1 will take a single activity value. Again, the output signal of the comparison layer C is set equal to exactly X, as in the beginning of the network. However, now the previous winner neuron is not participating in the competition in the recognition layer, and a new category will be found - the candidate. Then the comparison phase is repeated.
The iterative search process is completed in two possible ways.
It is important to understand why the search phase is generally required and the final result of the classification does not occur on the first attempt. The attentive reader has probably already found the answer to this question. Training and functioning of the ART network occurs simultaneously. In the space of the input vectors, the winning neuron determines the memory vector closest to the given input image, and if all the features of the original vector were critical, this would be a correct classification. However, many critical features stabilize only after relatively long training. At this phase of learning, only some components of the input vector belong to the actual set of critical features, so there may be another neuron classifier that will be closer to the original image on the set of critical features . It is determined by the search.
Note that after the relative stabilization of the learning process, the classification is performed without a search phase. In this case, it is said that direct memory access is being formed. The emergence in the process of learning direct access is proved in the theory of ART.
At the beginning of the operation, all the weights B and T of the neurons, as well as the similarity parameter, receive the initial values. According to the theory of ART, these values must satisfy the condition
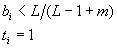
where m is the number of components of the input vector X, the value L> 1 (for example, L = 2). This choice of weights will lead to sustainable learning. The level of similarity r is selected based on the requirements of the problem being solved. At high values of this parameter, a large number of categories will be formed, each of which will include only very similar vectors. With a low level r the network will form a small number of categories with a high degree of generalization.
The learning process takes place without a teacher, based on self-organization. Training is performed for the weights of the winning neuron in the case of both successful and unsuccessful classification. In this case, the weights of the vector B tend to the normalized value of the components of the vector C:
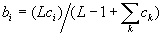
At the same time, the role of component normalization is extremely important. Vectors with a large number of units lead to small values of weights b, and vice versa. So the product
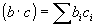
When applying the normalization, the original scalar products will be equal to unity for the neuron X1, and the value 2/5 for the neuron X2 (for L = 2). Thus, the neuron X1 deservedly and easily won the competitive competition.
Компоненты вектора T, как уже говорилось, при обучении устанавливаются равными соответвующим значениям вектора C. Следует подчеркнуть, что это процесс необратим. Если какая-то из компонент t j оказалась равной нулю, то при дальнейшем обучении на фазах сравнения соотвествующая компонента c j никогда не получит подкрепления от t j =0 по правилу 2/3, и, следовательно, единичное значение t j не может быть восстановлено. Обучение, таким образом, сопровождается занулением все большего числа компонент вектора T, оставшиеся ненулевыми компоненты определяют множество критических черт данной категории. Эта особенность проиллюстрирована на Рис. 11.3.
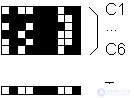
Fig. 11.3. Обучающие образы C и сформированный вектор критических черт T - минимальный набор общих элементов категории.
В оригинальной работе обучение рассматривается в терминах дифференциальных уравне-ний, из которых указанные нами значения получаются в виде предельных.
Остановимся теперь кратко на основных теоремах теории АРТ, характеризующих обучение и функционирование сети. Некоторые из них нами уже упоминались в тексте.
1. По достижении стабильного состояния обучения пред'явление одного из обучающих векторов будет сразу приводить к правильной классификации без фазы поиска, на основе прямого доступа.
2. Процесс поиска устойчив.
3. Процесс обучения устойчив. Обучение весов нейрона-победителя не приведет в дальнейшем к переключению на другой нейрон.
4. Процесс обучения конечен. Обученное состояние для заданного набора образов будет достигнуто за конечное число итерации, при этом дальнейшее пред'явление этих образов не вызовет циклических изменений значений весов.
Нейронные сети АРТ, при всех их замечательных свойствах, имеют ряд недостатков. Одним из них является большое количество синаптических связей в сети, в расчете на единицу запоминаемой информации. При этом многие из весов этих связей (например, веткора T) оказываются после обучения нулевыми. Эту особенность следует учитывать при аппаратных реализациях.
Сеть АРТ-1 приспособлена к работе только с битовыми векторами. Это неудобство преодолевается в сетях АРТ-2 и АРТ-3. Однако в этих архитектурах, равно как и в АРТ-1, сохраняется главный недостаток АРТ - локализованность памяти. Память нейросети АРТ не является распределенной, некоторой заданной категории отвечает вполне конкретный нейрон слоя распознавания. При его разрушении теряется память обо всей категории. Эта особенность, увы, не позволяет говорить о сетях адаптивной резонансной теории, как о прямых моделях биологических нейронных сетей. Память последних является распределенной.
Основной отличительной чертой нейронной сети АРТ-2 является возможность работы с аналоговыми векторами и сигналами. По сравнению с АРТ-1 в архитектуре сети сделаны некоторые изменения, позволяющие отдельным подсистемам функционировать асинхронно, что принципиально для аппаратных реализаций.
Важным отличием аналоговых сигналов от битовых является принципиальная возможность аналоговых векторов быть сколь угодно близкими друг к другу (в то время как простанство битовых векторов дискретно). Это накладывает дополнительные требования на функционирование нейронов слоя сравнения - требуется более тонкий и чувствительный механизм для выделения областей резонанса. Общим решением здесь является переход к многослойной архитектуре, с все более точной настройкой при переходе от слоя к слою, что и применено в АРТ-2. Функционирование слоя распознавания принципиально не изменяется.
Сети АРТ-2 применялись для распознавания движущихся изображений. Успешные эксперименты выполнены в Массачусетском Технологическом Институте (MIT). Поскольку нейросистемы АРТ не содержат механизма инвариантного распознавания (в отличие от НЕОКОГНИТРОНА, см. предыдущую Лекцию), то в сочетании с ними применяются специализированные (часто не нейросетевые) системы инвариантного представления образов, например двумерное преобразование Фурье, или более сложные алгоритмы. Более подробное рассмотрение особенностей и применений АРТ-2 требует профессионального изучения и не входит в наши цели.
Следующим шагом в развитии АРТ явилась сеть АРТ-3. Особенности обучения нейронов сетей АРТ-1 и АРТ-2 не позволяют использовать эти сети, как элементы более крупных иерархических нейросистем, в частности, компоновать из них многослойные сети. Это затрудняет представление в АРТ иерархически организованной информации, что характерно для систем восприятия человека и животных.
Эти проблемы решены в сети АРТ-3, которая выступает как многослойная архитектура. При переходе от слоя к слою происходит контрастирование входных образов и запоминание их в виде все более общих категорий. При этом основной задачей каждого отдельного слоя является сжатие входящей информации.
Образ входит в адаптирующийся резонанс между некоторой парой слоев, в дальнейшем этот резонанс рапространяется на следующие слои иерархии. В АРТ-1 и АРТ-2 недостаточный уровень резонанса приводил к генерации сигнала сброса, что приводило к полному торможению слоя распознавания. В случае многослойной сети АРТ-3 это недопустимо, так как это разрывает поток информации. Поэтому в АРТ-3 введен специальный механизм зависимости активности синапсов обратных связей от времени, аналогичный рефрактерному торможению биологического нейрона после передачи возбуждения. Поэтому вместо полного сброса сигнала происходит торможение синаптических сигналов обратной связи, и слой сравнения получает исходное состояние возбуждения для выполнения фазы поиска нового резонанса.
Интересным предложением является также использование в многослойной иерархии слоев, которые не являются слоями АРТ, а принадлежат некоторой другой архитектуре. В этом случае система получается гибридной, что может привести к возникновению новых полезных свойств.
Развитие теории АРТ продолжается. По высказыванию авторов теории, АРТ представляет собой нечто существенно более конкретное, чем философское построение, но намного менее конкретное, чем законченная программа для компьютера. Однако уже в современном виде, опираясь на свою более чем 20-летнюю историю, сети АРТ демонстрируют свои успешные применения в различных областях. АРТ сделала также важный шаг в общей проблеме моделирования пластично-стабильного восприятия.
Comments
To leave a comment
Computational Neuroscience (Theory of Neuroscience) Theory and Applications of Artificial Neural Networks
Terms: Computational Neuroscience (Theory of Neuroscience) Theory and Applications of Artificial Neural Networks