Biological neuron and its cybernetic model.

Neurobiology. Biological neuron, its structure and function. The union of neurons in the network. Biological variability and learnability of neural networks. The cybernetic model of a neuron is a formal McCulloch and Pitts neuron. Teaching a neuron the task of detecting the border of brightness.

This lecture is devoted to the biological basis of the science of computational neural networks. Also, as in the previous lecture, the presentation will be for reference only, and is intended for the reader who does not have special knowledge of biology. Deeper professional information can be found in the relatively recently translated book of N. Green, W. Stout and D. Taylor, as well as in the monograph by G. Shepherd. For introductory reading, we can recommend the book by F. Blum, A. Leiserson, and L. Hofstedter.

Throughout the book, our main goal will be the study of methods and cybernetic systems that simulate brain functions in solving information problems. This way of developing artificial computing systems seems to be natural in many respects - higher biological organisms, and especially humans, easily cope with such extremely difficult problems in mathematical analysis, such as, for example, pattern recognition (visual, auditory, sensory and other), memory and sustainable body movement control. The biological foundation for the study of these functions is extremely important, the natural diversity provides an extremely rich source material for the directional creation of artificial models.

At the end of the lecture, the classical cybernetic model of a neuron, the so-called McCulloch and Pitts formal neuron, will be presented. Some properties of a formal neuron will be studied on the problem of detecting the black-white transition boundary in a simple image.

Neurobiology method.

The subject of neurobilology is the study of the nervous system and its main organ - the brain. The principal issue for this science is the determination of the relationship between the structure of the nervous system and its function . In this case, the examination is carried out at several levels: molecular, cellular, at the level of a separate organ, of the organism as a whole, and further at the level of a social group. Thus, the classical neurobiological approach consists in the sequential advancement from elementary forms in the direction of their complication.

For our practical purposes, the starting point will be the cellular level. According to modern concepts, it is on it that the aggregate of elementary molecular chemical and biological processes in a separate cell forms it as an elementary processor capable of the simplest processing of information.

Biological neuron.

An element of the cellular structure of the brain is a nerve cell - a neuron . In its structure, a neuron has many common features with other biotissue cells: the body of a neuron is surrounded by a plasma membrane, inside which is the cytoplasm, the nucleus and other components of the cell. However, the nerve cell differs significantly from other in its functional purpose . The neuron performs reception, elementary transformation and further transmission of information to other neurons. Information is transferred in the form of impulses of nervous activity, having an electrochemical nature.

Neurons are extremely diverse in form, which depends on their location in the nervous system and the characteristics of functioning. In Fig. 3.1. shows the structure of a "typical" neuron. The cell body contains many branching processes of two types. The processes of the first type, called dendrites for their similarity to the crown of the spreading tree, serve as input channels for nerve impulses from other neurons. These impulses enter the soma or the cell body from 3 to 100 microns in size, causing its specific excitation, which then spreads along the outflow process of the second type - the axon . The length of axons usually markedly exceeds the size of dendrites, in some cases reaching tens of centimeters and even meters. The giant axon of squid has a thickness of about a millimeter, and it was his observation that served to clarify the mechanism of transmission of nerve impulses between neurons.

The body of the neuron, filled with a conductive ionic solution, is surrounded by a membrane with a thickness of about 75 angstroms, which has a low conductivity. An electric potential difference is maintained between the inner surface of the axon membrane and the external environment. This is accomplished using the molecular mechanism of ionic pumps, which create different concentrations of positive K ⁺ and Na ⁺ ions inside and outside the cell. The permeability of the membrane of the neuron is selective for these ions. Inside the axon of a cell at rest, active transport of ions tends to maintain the concentration of potassium ions higher than sodium ions, whereas in the fluid surrounding the axon, the concentration of Na ⁺ ions is higher. Passive diffusion of more mobile potassium ions leads to their intense release from the cell, which causes its total negative potential relative to the external environment, which is about -65 millivolts.

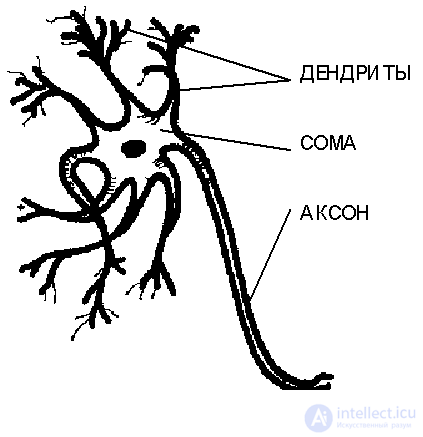
Fig. 3.1. The general scheme of the structure of a biological neuron.

Under the influence of stimulating signals from other neurons, the axon membrane dynamically changes its conductivity. This occurs when the total internal potential exceeds the threshold value of the scale -50 mV. The membrane for a short time of about 2 milliseconds changes its polarity (depolarized) and reaches an action potential of about +40 mV. At the micro level, this is due to the short-term increase in membrane permeability to Na ⁺ ions and their active entry into the axon. Later, as the potassium ions come out, the positive charge from the inner side of the membrane changes to a negative one, and the so-called refractoriness period lasts for about 200 ms. During this time, the neuron is completely passive, almost invariably maintaining the potential inside the axon at about -70 mV.

A cell membrane depolarization impulse, called a spike , propagates along the axon with little or no attenuation, supported by local ionic gradients. The speed of the spike is relatively low and ranges from 100 to 1000 centimeters per second.

The excitation of a neuron in the form of a spike is transmitted to other neurons, which are thus combined into a network that conducts nerve impulses. The membrane sections on the axon, where the contact areas of the axon of a given neuron with the dendrites of other neurons are located, are called synapses . In the area of ​​the synapse, which has a complex structure, there is an exchange of information about the excitation between neurons. The mechanisms of synaptic transmission are quite complex and diverse. They can be of chemical and electrical nature. The chemical synapse in the transmission of impulses involves specific chemicals - neurotransmitters , which cause changes in the permeability of the local membrane section. Depending on the type of mediator produced, a synapse may have a stimulating (effectively conducting excitation) or inhibiting effect. Usually, the same mediator is produced on all the processes of a neuron, and therefore the neuron as a whole is functionally inhibitory or exciting. This important observation about the presence of various types of neurons in subsequent chapters will be significantly used in the design of artificial systems.

Neural networks.

Neurons interacting with each other through transmission through processes of excitations form neural networks . The transition from a separate neuron to the study of neural networks is a natural step in the neurobiological hierarchy.

The total number of neurons in the human central nervous system reaches 10 ¹⁰ - 10 ¹¹ , with each nerve cell associated with an average of 10 ³ - 10 ⁴ other neurons. It has been established that in the brain a collection of neurons in a volume of 1 mm ³ scale forms a relatively independent local network carrying a certain functional load.

There are several (usually three) basic types of neural networks that differ in structure and purpose. The first type consists of hierarchical networks, often found in the sensory and motor pathways. Information in such networks is transmitted in the course of a sequential transition from one level of hierarchy to another.

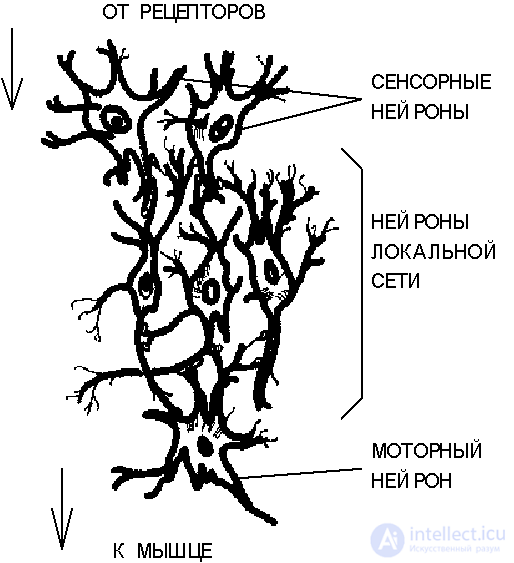
Fig. 3.2.The structure of a simple reflex neural network.

Neurons form two characteristic types of connections - convergent , when a large number of neurons of one level come into contact with a smaller number of neurons of the next level, and divergent , in which contacts are established with an increasing number of cells of subsequent layers of the hierarchy. The combination of convergent and divergent connections provides multiple duplication of information paths, which is a decisive factor in the reliability of the neural network. With the death of part of the cells, the remaining neurons are able to maintain the functioning of the network. The second type of neural networks includes local networks formed by neurons with limited spheres of influence. LAN neurons produce information processing within the same hierarchy level. At the same time, a functionally local network is a relatively isolated inhibitory or exciting structure. An important role is also played by the so-called divergent networks with one input . A command neuron located at the base of such a network can affect immediately a multitude of neurons, and therefore single-input networks act as a matching element in a complex combination of neural network systems of all types.

Consider schematically a neural network that forms a simple reflex chain with the transfer of excitation from the stimulus to the motor muscle (Fig. 3.2).

The signal of an external stimulus is perceived by sensory neurons associated with sensitive receptor cells. Sensory neurons form the first (lower) level of the hierarchy. The signals generated by them are transmitted to local network neurons, which contain many direct and reverse connections with a combination of divergent and convergent connections. The nature of the signal transformed in local networks determines the state of excitation of motor neurons. These neurons, which constitute the upper level of the hierarchy in the network under consideration, figuratively speaking, “make a decision”, which is expressed in the effect on muscle cells by means of neuromuscular connections.

Biological variability and training of neural networks.

The structure of the main types of neural networks is genetically predetermined. At the same time, research in the field of comparative neuroanatomy suggests that according to the fundamental plan of the structure of the brain, very little has changed in the process of evolution. However, deterministic neural structures exhibit variability properties that determine their adaptation to specific conditions of functioning.

Genetic predestination also occurs in relation to the properties of individual neurons, such as, for example, the type of neurotransmitter used, the shape and size of the cell. Variability at the cellular level is manifested in the plasticity of synaptic contacts. The nature of the metabolic activity of the neuron and the permeability properties of the synaptic memran may vary in response to long-term activation or inhibition of the neuron. Synaptic contact "trains" in response to the conditions of functioning.

Variability at the network level is related to the specificity of neurons. Nervous tissue is practically devoid of the ability for other types of tissues to regenerate by cell division. However, neurons demonstrate the ability to form new processes and new synaptic contacts. A series of experiments with intentional damage to the nerve pathways indicates that the development of neural branches is accompanied by competition for the possession of synaptic sections. This property as a whole ensures the stability of the functioning of neural networks with the relative unreliability of their individual components - neurons.

The specific variability of neural networks and the properties of individual neurons underlies their ability to learn - to adapt to the conditions of functioning - with their morphological structure as a whole. It should be noted, however, that consideration of the variability and learnability of small groups of neurons does not generally allow answering questions about learning at the level of higher forms of mental activity associated with intelligence, abstract thinking, and speech.

Before turning to the consideration of models of neurons and artificial neural networks, let us formulate general factual statements about biological neural networks. Here we fully follow what has been stated in the book by F. Blum, A. Leyzerson and L. Hofstedter.

The main active elements of the nervous system are individual cells, called neurons. They have a number of common features with cells of other types of features, and they are very different from them in their configuration and functional purpose. The activity of neurons in the transmission and processing of nerve impulses is regulated by membrane properties, which may change under the influence of synaptic mediators. The biological functions of the neuron can change and adapt to the conditions of functioning. Neurons integrate into neural networks, the main types of which, as well as the pathways of the brain, are genetically programmed. In the process of development, a local modification of neural networks with the formation of new connections between neurons is possible. Note also that the nervous system contains, in addition to neurons, cells of other types.

Formal neuron.

Historically, the first work that laid the theoretical foundation for creating artificial models of neurons and neural networks is considered to be the logical calculation of ideas related to nervous activity, published in 1943 by Warren S. Mac-Callock and Walter Pitts. The main principle of the theory of McCulloch and Pitts is that arbitrary phenomena related to higher nervous activity can be analyzed and understood as some activity in a network consisting of logical elements that accept only two states (“all or nothing”). Moreover, for any logical expression that satisfies the conditions specified by the authors, a network of logical elements can be found that has the behavior described by this expression. Discussion questions concerning the possibility of modeling the psyche, consciousness, etc. are beyond the scope of this book.

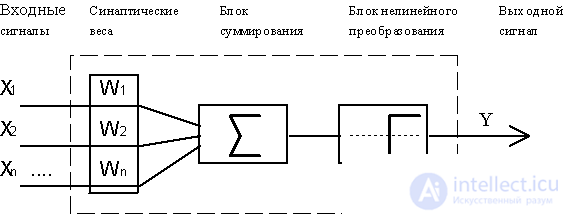
Fig.4.1. Functional diagram of the formal necron McCulloch and Piitsa.

As a model of such a logical element, later called the "formal neuron", the scheme shown in Fig. 4.1. From the modern point of view, a formal neuron is a mathematical model of a simple processor with several inputs and one output. The vector of input signals (coming through the "dendrides") is converted by the neuron into the output signal (propagating along the "axon") using three functional blocks: local memory, summation unit and non-linear conversion unit.

The local memory vector contains information about the weighting factors with which the input signals will be interpreted by the neuron. These variable weights are analogous to the sensitivity of plastic synaptic contacts. The choice of weights is achieved by one or another integral function of the neuron.

In the summation block, a common input signal (usually denoted by the symbol net ) is accumulated, equal to the weighted sum of the inputs:

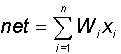
In the McCulk and Pitts model there are no time delays of the input signals, therefore the net value determines the total external excitation perceived by the neuron. The response of the neuron is further described on the "all or nothing" principle, i.e., the variable is subjected to a non-linear threshold transformation, in which the output (activation state of the neuron) Y is set to unity if net> Q , and Y = 0 in the opposite case. The threshold value Q (often assumed to be zero) is also stored in local memory.

Fomal neurons can be networked by closing the outputs of some neurons to the inputs of others, and according to the authors of the model, such a cybernetic system with appropriately selected weights can represent an arbitrary logical function. For the theoretical description of the resulting neural networks, the mathematical language for calculating logical predicates was proposed.

It should be noted that today, 50 years after the work of McCulloch and Pitts, there seems to be no exhaustive theory of the synthesis of logical neural networks with an arbitrary function. The most advanced were research in the field of multilayer systems and networks with symmetric connections. Most models rely on various modifications of the formal neuron. An important development of the formal neuron theory is the transition to analog (continuous) signals, as well as to various types of non-linear transition functions. We describe the most widely used types of transition functions Y = f (net).

• Threshold function (reviewed by McCulloch and Pitts):

  

• Linear function, as well as its version - a linear function with the repayment of negative signals:

  

• Sigmoidal function:

  

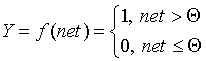
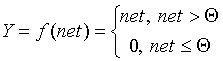
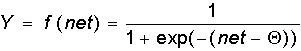
As indicated by S. Grossberg, the sigmoidal function has a selective sensitivity to signals of different intensity, which corresponds to biological data. The highest sensitivity is observed near the threshold, where small changes in the net signal lead to tangible changes in the output. On the contrary, the sigmoidal function is not sensitive to signal variations in areas significantly higher or lower than the threshold level, since its derivative tends to zero for large and small arguments.

Recently, mathematical models of formal neurons, which take into account non-linear correlations between inputs, are also being considered. Electrotechnical analogues have been proposed for McCulloch and Pitts neurons, allowing direct hardware simulation.

Teaching a neuron to detect the black-white border

The ability of a formal neuron to learn is manifested in the possibility of changing the values ​​of the weights vector W, corresponding to the plasticity of the synapses of biological neurons. Consider the training of a formal neuron on the example of the simplest problem of border detection. Suppose there is an image composed of a one-dimensional chain of black and white cells. Blackened cells correspond to a single signal, while white cells correspond to a single signal. The signal at the inputs of the formal neuron is set equal to the values ​​of pairs of adjacent cells of the image in question. A neuron learns to be excited every time and to produce a single output signal, if its first input (in Fig. 4.2. - left) is connected to a white cell, and the second (right) input - to a black one. Thus, the neuron should serve as a detector of the border of the transition from light to dark tone of the image.

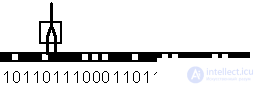
Fig. 4.2. A formal neuron with two entrances, busy processing the image in the form of a one-dimensional chain of black and white cells.

The function performed by the neuron is defined by the following table.

For this task, the values ​​of weights and the threshold of the neuron can be presented without a special training procedure. It is easy to make sure that the necessary requirements are met by the set Q = 0, W ₁ = -1, W ₁ = +1. In the case of the problem of detecting the boundary of the transition from dark to light weight, you need to swap places.

In the general case, various algorithms have been developed for adjusting weights when training a neuron, which will be considered as applied to specific types of neural networks composed of formal neurons.