ANALYSIS OF THE ALGORITHM FOR REVERSE DISTRIBUTION OF NEURAL NETWORK ERROR

The article outlines the basics of the neural network, and also analyzes the operation of the back-propagation error algorithm.

Today, the neural network is one of the ways of data mining. Intelligent data analysis allows to solve such problems as: classification and clustering, forecasting, pattern recognition, data compression and associative memory, diagnosis of diseases, etc.

Neural networks are one of the areas of research in the field of artificial intelligence, based on attempts to reproduce the human nervous system. Namely, the ability of the neural network to learn and correct errors, which should allow to simulate, although quite roughly, the work of the human brain [1].

The neural network is a mathematical model of the human brain, consisting of many simple computing elements (neurons) Figure 1, working in parallel, the function of which is determined by the structure of the network, and the calculations are performed in the elements themselves. It is believed that the ability of the brain to process information is mainly due to the functioning of networks consisting of such neurons [1; 2].

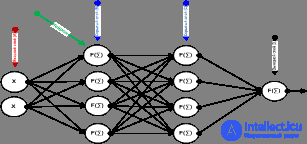
Figure 1. Multilayer neural network

Consider a neural network of a standard architecture (Figure 1), which usually has several layers: A, the receptor layer, to which input data are supplied; B, C - hidden layers whose neurons interpret the received information; D is the output layer providing the response of the neural network.

Each layer of the network consists of neurons. The neuron is the main element of the computation, the neural network. Figure 2 shows its structure.

The structure of the neuron includes multipliers, adders and a nonlinear converter. Synapses communicate between neurons and multiply the input signal by a number characterizing the strength of the connection - the weight of the synapses.

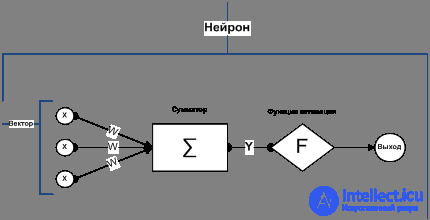
Picture. 2. Structure of an artificial neuron

The adder performs the addition of signals received via synoptic connections from other neurons or external input signals. The non-linear converter implements a non-linear function of one argument - the output of the adder. This function is called the “ activation function ” or “ transfer function ” of the neuron. The neuron as a whole implements the scalar function of the vector argument.

The mathematical model of a neuron describes the relations

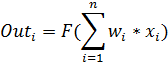
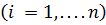where - synapse weight ; s is the result of summation; x _i   - component of the input vector ;

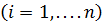y is the output of the neuron; n is the number of inputs of the neuron; F — activation function;

The main task in the process of developing a neural network is the training phase, i.e., adjusting the weights of the network to minimize the error at the output of the neural network.

A standard direct propagation neural network is shown in Figure 3, also known as multilayer perceptron (MLP). Note that input level nodes are different from nodes in other layers, which means that no processing takes place at these nodes, they serve only as inputs to the network.

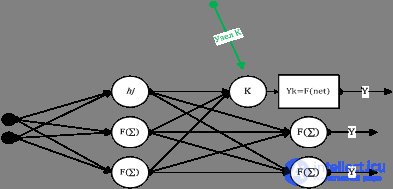
Figure 3. Standard direct distribution network

Each node calculates a weighted sum of its inputs, and uses it as input to the transform function.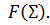

In the classical multilayer perceptron, the transformation function is sigmoid.

Sigmoid   -   it is a smooth monotone non-linear S-shaped function, which is often used to “ smooth out ” the values ​​of a certain value.

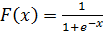(one)

Consider the node k in the hidden layer. Its output yk represents 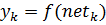where f, the activation function (sigmoid), is the weighted sum of the outputs of the nodes of the input layer A

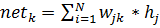(2)

similarly, the output of each node in each layer.

For convenience, we can consider the network inputs as the input vector X, where 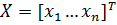. Similarly, the output for the network can be considered as an output vector, Y where 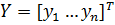. A training set for the network can be represented by a series of pairs of K input xi vectors and the desired output vectors: .

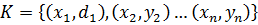Every time the input vector from the training set 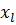applied to the network, the network produces the actual output 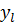. We can thus determine the quadratic error for this input vector by summing the quadratic errors at each output node [3; four]: 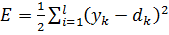. (3)

The main task, as was already said in the training of the neural network, is to minimize the quadratic error of E. We can also determine the total quadratic error, summarize all the pairs of input - output in the training set:

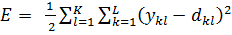(four)

To minimize the quadratic error, we will use the gradient descent algorithm. Determine which direction is the “downhill” on the surface of errors and change each weight so that we move in this direction. Mathematically, this means that each weight will be changed by a small amount in the direction of decreasing:

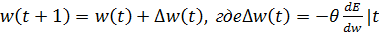(five)

Here 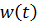- weight at time t and 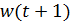- updated weight. Equation 5 is called the generalized delta rule. To perform a gradient descent, you need to find the partial derivative of each weight.

To adjust the weights, between the hidden and the output layer, you need to find the partial derivative for each node of the output layer.

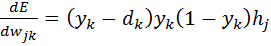(6)

Thus, the partial derivative of error E by weights was found. 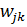and we can use this result in equation 5 to perform a gradient descent for all weights between the hidden and output layers.

Now consider the weights, between the input layer and the hidden layer.

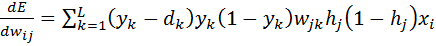(7)

The partial derivative of the error E by weight was obtained on the basis of known quantities (many of which we have already calculated when obtaining ).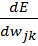

Consider the algorithm back propagation of errors in the form of a flowchart (Figure 4).

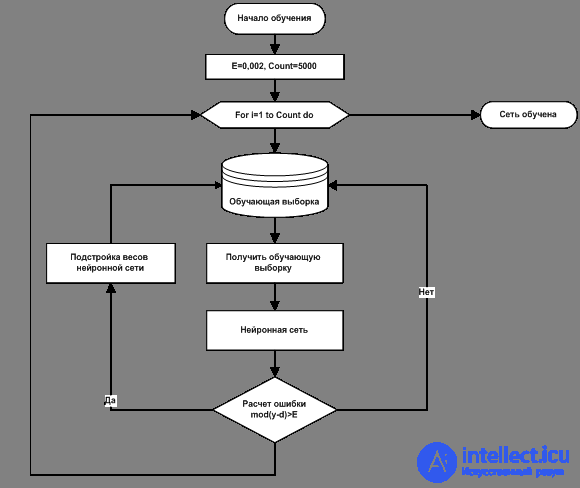
Figure 4. Learning algorithm of direct distribution neural network

The principle of the back-propagation algorithm for error, is to use the method of gradient descent and adjust the weights, to minimize the error of the neural network.

In the process of developing a neural network, one of the main stages is the training of a neural network. In this article, an analysis was performed of the back-propagation error algorithm, which uses the gradient descent method, to adjust the weights.

Bibliography:
1. Russell S., Norvig P. Artificial Intelligence. Modern approach. - M .: Publishing house "Williams", 2006. - 1408 p.
2. Khaikin S. Neural networks: a full course. - M .: Publishing house "Williams", 2006. - 1104 p.
3. Algorithm back propagation errors. - [Electronic resource] - Access mode. - URL: http: //www.aiportal.ru/articles/neural-networks/back-propagation.
4. The algorithm back propagation of errors. - [Electronic resource] - Access mode. - URL: http: //masters.donntu.edu.ua/2006/kita/kornev/library/l10.htm.