10. NEOKOGNITRON Fukushima.

KOGNITRON and NEOKOGNITRON Fukushima. Learning rules Invariant pattern recognition by NEOKOGNITRONOM.

In this lecture, we turn to the consideration of some relatively new modern architectures, among which, above all, NEOKOGNITRON and its modifications should be noted. In the next lecture, we will discuss options for networks built on the theory of adaptive resonance (ART).

COGNITRON: self-organizing multilayer neural network.

The creation of KOGNITRON (K.Fukushima, 1975) was the fruit of a synthesis of the efforts of neurophysiologists and psychologists, as well as specialists in the field of neurocybernetics, jointly engaged in the study of the human perception system. This neural network is simultaneously both a model of perceptual processes at the micro level and a computing system used for technical tasks of pattern recognition.

COGNITRON consists of hierarchically connected layers of neurons of two types - inhibitory and excitatory. The excitation state of each neuron is determined by the sum of its inhibitory and exciting inputs. Synaptic connections go from the neurons of one layer (further layer 1) to the next (layer 2). Regarding this synaptic connection, the corresponding neuron of layer 1 is presynaptic, and the neuron of the second layer is postsynaptic. Postsynaptic neurons are not connected with all neurons of the 1st layer, but only with those that belong to their local area of ​​connections . The regions of connections of postsynaptic neurons close to each other overlap, therefore the activity of this presynaptic neuron will affect the ever expanding region of postsynaptic neurons of the next layers of the hierarchy.

The input of the exciting postsynaptic neuron (in Fig. 10.1 - neuron i ) is determined by the ratio of the sum E of its exciting inputs (a1, a2 and a3) to the sum I of inhibitory inputs (b1 and the input from neuron X):

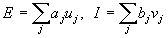
where u - excitation inputs with weights a , v - braking inputs with weights b . All weights are positive. Using the values ​​of E and I, the total impact on the i -th neuron is calculated: net _i = ((1 + E) / (1 + I)) - 1 . Its output activity u _{i is} then set to net _i if net _i > 0. Otherwise, the output is set to zero. Analysis of the formula for the total effect shows that with a small inhibition of I, it is equal to the difference between the exciting and inhibiting signals. In the case when both of these signals are large, the effect is limited by the ratio. Such features of the reaction correspond to the reactions of biological neurons capable of operating in a wide range of effects.

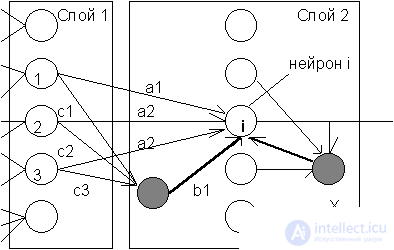
Presynaptic inhibitory neurons have the same binding region as the excitatory postsynaptic neuron i under consideration. At the same time, the weights of such inhibiting neurons (c1, c2, and c3) are given and do not change during training. Their sum is equal to one, thus, the output of the inhibitory presynaptic neuron is equal to the average activity of excitatory presynaptic neurons in the field of connections:

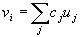
Learning the weights of the excitatory neurons takes place according to the principle “the winner takes all” in the field of competition - a certain neighborhood of the excitatory neuron. At this step, only the weights a _{i of the} neuron with the maximum excitation are modified:

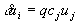
where c _j is the inhibiting weight of the neuron connection j in the first layer, u _j is the state of its excitation, q is the learning coefficient. The weights of the inhibitory neuron i of the second layer are modified in proportion to the ratio of the sum of the exciting inputs to the sum of the inhibiting inputs:

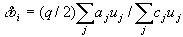
In the case when there is no winner in the field of competition (on layer 2), as is the case, for example, at the beginning of training, the weights are adjusted according to other formulas:

This learning procedure leads to a further increase in the excitatory connections of active neurons and inhibition of passive ones. In this case, the weights of each of the neurons in layer 2 are adjusted to some image, often presented during training. A new appearance of this image will cause a high level of excitation of the corresponding neuron, with the appearance of other images, its activity will be low and will be suppressed during lateral inhibition.

The weights of neuron X performing lateral inhibition in the area of ​​competition are non-modifiable, their sum is equal to one. In this case, in the second layer, iterations are performed that are similar to competitive iterations in the Lippmann-Hamming network, which we considered in 7 lectures.

Note that the overlapping areas of competition of similar neurons in the second layer contain a relatively small number of other neurons, so a particular winning neuron cannot decelerate the entire second layer. Consequently, in competition, several neurons of the second layer can win, providing a more complete and reliable processing of information.

In general, KOGNITRON is a hierarchy of layers that are sequentially connected with each other, as discussed above for a pair of layer 1 - layer 2. In this case, the neurons of the layer form not a one-dimensional chain, as in Fig. 10.1, and cover the plane, similar to the layered structure of the human visual cortex. Each layer realizes its own level of information synthesis. Input layers are sensitive to individual elementary structures, for example, lines of a certain orientation or color. Subsequent layers already react to more complex generalized images. At the highest level of the hierarchy, active neurons determine the result of the network operation — recognition of a particular image. For each largely new image, the image of the activity of the output layer will be unique. At the same time, it will be preserved even if a distorted or noisy version of this image is displayed. Thus, information processing by COGNITRON takes place with the formation of associations and generalizations.

The author of COGNITRON Fukushima this network was used for optical character recognition - Arabic numerals. The experiments used a network with 4 layers of neurons arranged in 12 x 12 matrices with a square connection area of ​​each neuron 5 x 5 in size and a rhombus-shaped competition area with a height and width of 5 neurons. The learning parameters were q = 16, q '= 2. As a result, successful learning of the system in five figures was obtained (similar to the pictures with letters that we considered for the Hopfield network), and it took about 20 training cycles for each picture.

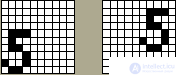
Despite successful applications and numerous advantages, such as the correspondence of the neurostructure and mechanisms for teaching biological models, the parallelism and hierarchy of information processing, the distribution and associativity of memory, etc., COGITRON has its drawbacks. Apparently, the main one is the inability of this network to recognize images that are displaced or rotated relative to their original position. For example, two pictures in Fig. 10.2 from the point of view of a person are undoubtedly images of the same figure 5, however COGITITRON is not able to catch this similarity.

Recognition of images, regardless of their position, orientation, and sometimes size and other deformation, is said to be invariant with respect to the corresponding transformations of recognition. Further research of the group led by K. Fukushima led to the development of COGNITRON and the development of a new neural network paradigm - NEOKOGNITRON, which is capable of invariant recognition.

NEOKOGNITRON and invariant pattern recognition.

The new work of Fukushima was published in 1980 by NEOKOGNITRON, although it has many features in common with its progenitor COGNITRON, but at the same time it has undergone significant changes and complications in accordance with the advent of new neurobiological data (Hubel DH, Wiesel TN, 1977, etc.) .

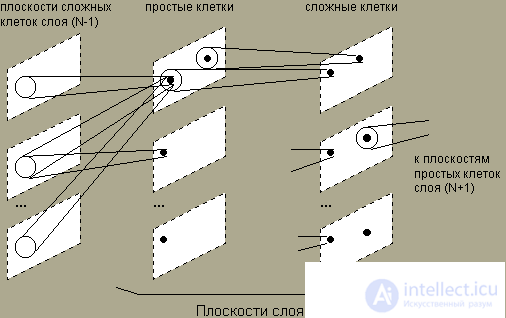
NEOKOGNITRON consists of a hierarchy of neural layers, each of which consists of an array of planes. Each array element consists of a pair of neuron planes. The first plane consists of the so-called simple neural cells, which receive signals from the previous layer and highlight certain images. These images are further processed by complex neurons of the second plane, the task of which is to make the selected images less dependent on their position.

The neurons of each pair of planes are trained to respond to a particular image, presented in a certain orientation. For a different image or for a new angle of rotation of the image, a new pair of planes is required. Thus, with large volumes of information, NEOKOGNITRON is a huge structure with a large number of planes and layers of neurons.

Simple neurons are sensitive to a small area of ​​the input image, called the receptive area (or, equivalently, the area of ​​connections). A simple neuron comes to an excited state if a certain image appears in its receptive area. The receptor areas of simple cells overlap and cover the entire image. Complex neurons receive signals from simple cells, while a single signal from any simple neuron is sufficient to excite a complex neuron. Thus, a complex cell registers a certain image regardless of which of the simple neurons performed detection, and therefore, regardless of its location.

As information spreads from a layer to a layer, the picture of neural activity becomes less and less sensitive to the orientation and location of the image, and, within certain limits, to its size. The neurons of the output layer perform the final invariant recognition.

The training of NEOCHRITRON is similar to the already reviewed COGNITRON training. When only the synaptic weights of simple cells change. Braking neurons instead of the average activity of neurons in the field of connections use the square root of the weighted sum of squares of the inputs:

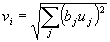
Such a formula for inhibiting cell activity is less sensitive to the size of the image. After selecting a simple neuron, the weights of which will be trained, it is considered as a representative of the layer, and the weights of all other neurons will be trained according to the same rules. Thus, all simple cells are trained in the same way, giving the same reaction to identical images in recognition.

In order to reduce the volume of information processed, the resolving fields of neurons expand from layer to layer, while the number of neurons decreases. In the output layer on each plane there is only one neuron, the receptive field of which covers the entire field of the image of the previous layer. In general, the functioning of NEOCONATRON is as follows. Copies of the input image are received on all planes of simple cells of the first layer. Further, all planes operate in parallel, passing information to the next layer. Upon reaching the output layer, in which each plane contains one neuron, some final distribution of activity occurs. The recognition result is indicated by that neuron, whose activity turned out to be maximum. At the same time, different recognition results will correspond to significantly different input images.

NEOKOGNITRON successfully manifested itself in character recognition. It should be noted that the structure of this network is extremely complex, and the computing volume is very large, so the computer models of NEOCOGNITRON will be too expensive for industrial applications. A possible alternative is, of course, switching to hardware or optical implementations, but their consideration is beyond the scope of this book.