Genetic search. Fuzzy logic systems. Cellular automata and neural networks.

Introduction to evolutionary algorithms. Combinatorial optimization by genetic search. Neural networks with fuzzy logic. State machines and neural networks.

Methods of analyzing information using a computer are constantly being improved. At the same time, along with the well-established and widely used methods of mathematical modeling, other non-traditional approaches are increasingly developed and used. One of them, associated with artificial neural networks, is the main subject of this book.

For completeness, the author found it necessary to give a brief overview of other methods, and, above all, genetic algorithms, systems with fuzzy logic and cellular automata. In order not to violate the integrity of the presentation, these methods will be considered in their correlation with neural network algorithms.

Genetic search.

Success in the development of neural networks is not least due to deep biological foundations embedded in many architectures. Some features of biological evolution, at the level of the coding and inheritance mechanism in DNA, formed the basis of the so-called genetic algorithms proposed in the early 70s (JH Holland, 1975) and have received intensive development in recent years.

An arbitrary object or system (in biology, an organism) can be described by a combination of features or traits that are encoded by a chain of characters or bits and constitute the genotype of the object. Several objects form a population characterized by a set of chains of each of the objects, the totality of which determines the gene pool of a population.

Different objects may, generally speaking, have different sets of features. A wide variety of traits and populations are spoken of as a rich gene pool. With the evolution of the population, new objects appear in it, inheriting certain characteristics from their ancestors. At the same time, the size of the population as a whole varies little, which is ensured by the competitive selection of objects. In the selection process, a directed search for such features or their aggregates (codons and genes), which are valuable in the sense of some given objective function , for example, the level of an object's adaptation to the conditions of existence, is made. Therefore, evolutionary algorithms are also called genetic search methods.

Information processing by a genetic algorithm uses two basic mechanisms for selecting useful traits borrowed from modern ideas about natural selection: mutations in a separate chain and crossing (crossing over) between two chains. Consider these mechanisms in more detail.

Figure A2.1. The process of crossing two genetic chains.

Figure A2.2 shows the successive stages of the exchange of information between two chains when crossing. The obtained new chains (or one of them) can be further included in the population, if the set of features given by them gives the best value of the objective function. Otherwise, they will be eliminated, and their ancestors will remain in the population. A mutation in a genetic chain has a point character: at some random point of the chain, one of the codes is replaced by another (zero - one, and one - zero).

From the point of view of artificial information processing systems, genetic search is a specific method for finding a solution to an optimization problem. At the same time, such an iterative search is adaptable to the features of the objective function: the chains that are born in the process of crossing test increasingly wide areas of feature space and are mostly located in the optimum area. Relatively rare mutations prevent the degeneration of the gene pool, which is equivalent to a rare, but not ceasing search for optimum in all other areas of the feature space.

A genetic algorithm can be used to train a neural network. In this case, the chain encodes the state of the network — the set of all weight coefficients. The code can be arranged as follows. The first eight elements of the chain correspond to the 8-bit representation of the first element of the weights matrix, the next eight to the second, and so on. The target function is the complete training error. The population of neural networks evolves to a trained state, while in the selection process, chains encoding neural networks with small errors survive.

The genetic algorithm is an example of a problem that allows a high degree of parallelism in modeling on modern vector computers. The simplicity of the operations performed also opens up broad prospects for the development of specialized genetic processors .

Fuzzy logic systems.

Fuzzy logic is a generalization of the usual Boolean logic that operates on binary numbers that correspond to the concepts of truth and falsehood . In fuzzy logic, these concepts are generalized to all intermediate states between truth and falsehood. In accordance with this, fuzzy logic operates with numbers from the interval [0,1], which reflect the degree of truth of the statement. For the first time, the theory of fuzzy sets was formulated by Zadeh, a professor at the University of California.

Fuzzy logic is based on many practical needs of applied sciences, operating with incompletely reliable and contradictory information. These include the theory of management and decision-making on incomplete information, system ecology, dealing with risk assessments of the anthropogenic impact of industrial production and the consequences of accidents, macroeconomics, and others.

The transition from the binary representation of numbers to the interval requires the generalization of logical operations to the corresponding operations with fuzzy numbers. In this case, the generalized operations should go into the classical, if the operands have values ​​of 0 or 1.

Consider an example of such a generalization. Suppose there are fuzzy numbers a and b. The sum of two fuzzy numbers is called a fuzzy number that coincides with the maximum operand: c = a + b = max (a, b). The product of two fuzzy numbers is called a fuzzy number equal to the minimum operand: c = a * b = min (a, b). In accordance with the definitions introduced, the set of fuzzy numbers is closed with respect to these operations.

One of the important applications of fuzzy logic is fuzzy expert systems (NES), in which logical rules of inference operate on fuzzy operations. For acquaintance with NES and other applications of fuzzy logic, we can recommend the book of Japanese authors T. Terano, K. Asai and M. Sugeno.

In this part of the book we will focus on the formulation of neural network models in the language of fuzzy logic. In the Hopfield model (Lecture 8) with network training according to the Habb rule, all calculations are based on addition and multiplication operations. If we describe the values ​​of weights and neuron activity by fuzzy numbers, then the Habb rule can be formulated in the language of fuzzy operations. The contribution to the matrix of relations from the image x ^(k) takes the form:

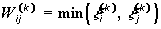
The full matrix of relations is obtained by fuzzy summation of individual contributions:

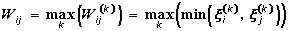
The neuron activity is calculated on using the scalar product:

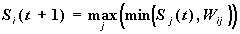
The Hopfield neural network presented in fuzzy arithmetic is very convenient for modeling using conventional shadow optics. Operands can be represented by rectangular holes, the areas of which are proportional to the values ​​of numbers.

To multiply the number of holes should be superimposed on each other, while the transmission of light will be limited to the minimum hole, which gives the desired product. When adding, two parallel beams of light should be focused on one plane, each of which is passed independently through one of the holes. The resulting light spot will correspond to the maximum opening. The corresponding optical scheme of the Hopfield network was proposed and published in the journal Optics Letters.

It should be noted that the optical realization of the Hopfield neural network with the fuzzy Habb rule naturally has a high computation speed and a high level of parallelism.

Cellular automata and neural networks.

A cellular automaton is a network of elements that change their state at discrete points in time, depending on the state of the element itself and its closest neighbors at the previous time point.

Different cellular automata can exhibit very diverse behaviors that can be adapted for information processing purposes by choosing (a) the law of state change of an element and (b) a specific definition of the term “nearest neighbors”. An attentive reader will easily notice that, for example, the Hopfield neural network may well be regarded as a cellular automaton whose elements are formal neurons. The threshold transformation of the weighted sum of the inputs of neurons is used as a law for changing the state of a neuro-automaton, and all other elements of the automaton are the nearest neighbors of each element.

In the world of cellular automata, there is a classification (S. Wolfram, 1983), according to which all automata are divided into four classes, depending on the type of dynamics of changing states. After the end of time, automata of the first class reach a homogeneous state in which the values ​​of all elements are the same and do not change with time. The second class of automata includes systems leading to localized structures of stationary or time-periodic element states. The third class consists of “wandering” automata, which over time visit in a random (non-periodic) manner all possible states of the elements, without lingering in one of them. And, finally, the fourth class consists of “strange” automata, the nature of the dynamics of which depends on the characteristics of the initial state of the elements. Some initial states lead to a homogeneous degeneration of the automaton, others to the occurrence of a cyclic sequence of states, and others to a continuously changing (both “through the system” and without a visible system) patterns of activity of the elements.

The fourth type of machine guns is the famous game “Life” by J. Conway. Each element (organism) of the colony of “Life” can be in a state of rest or activity. Four of his neighbors on a square lattice are declared closest to this element. The resting element can be revived to activity if there are exactly three active neighbors next to it. The active element retains “viability” with two active neighbors. If there are more than two neighbors, then the element perishes from cramping, and if there are less than two neighbors, then death comes from boredom. Although observing the complex evolution of the initial state of “Life” can provide some food for mental research, in general, this automaton remains nothing more than a mathematical curiosity.

There are, however, more serious applications of cellular automata. Among them, first of all, we should single out automata that implement discrete difference schemes for solving various problems of mathematical physics. For these purposes, automata of the second kind are used.

The activity of a population of automaton elements can also describe such complex phenomena as crystal growth from germinal states, diffusion and fluid migration in a heterogeneous porous medium, features of the occurrence and development of turbulence about fluid flows and gases, impulse propagation in the nervous system, tumor growth in biological tissue, the development of forest fires and other phenomena. The description of various applications of cellular automata deserves special attention.

However, this is already the subject of another book.

Tasks.

1. Formulate the task of finding the minimum of the function f (x) = (x-0.5) ² on the interval [0,1] for the genetic algorithm.

2. What type of cellular automata is the classic Hopfield neural network? What is the type of automaton given by a probabilistic generalization of the Hopfield network (Lecture 9) at very high temperatures? Why?