7. Other hierarchical architectures.

Command neurons and neurons-detectors Grossberg. The principle "Winner Takes All" (WTA). The Lippmann-Hemming model. Kohonen self-organization map. Counter Propagation Networks.

In this lecture various components of homogeneous (consisting of neurons of the same type) and inhomogeneous neural networks will be considered. Some advantages of hierarchical architectures — a more developed ability to generalize, the absence of rigid restrictions on the types of representable mappings while preserving the simplicity of the neural function and the properties of massive parallelism in information processing — have already been studied in a lecture devoted to a multi-layer back-propagation method of error propagation. Now we will get acquainted with other approaches to the construction of neural networks and teaching methods, and in particular, with the method of teaching without a teacher based on self-organization.

Grossberg Stars

The ideas reflected in the research of Stefan Grossberg at the dawn of biological cybernetics are the basis of many subsequent neural network developments. Therefore, we begin our consideration of hierarchical architectures with the configurations of input and output Grossberg stars (S. Grossberg, 1969).

A neuron in the shape of an input star has N inputs X ₁ ..X _N , which correspond to weights W ₁ ..X _N , and one output Y, which is the weighted sum of the inputs. The input star is trained to produce a signal at the output whenever a certain vector arrives at the inputs. Thus, the input star is a detector of the cumulative state of its inputs. The learning process is presented in the following iterative form:

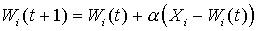
The learning rate a has an initial value of the scale of 0.1 and gradually decreases in the learning process. In the process of setting the neuron learns averaged training vectors.

The Grossberg output star performs the opposite function - the function of the command neuron, producing a certain vector at the outputs when a signal arrives at the input. A neuron of this type has one input and M outputs with weights W1..M, which are trained according to the formula:

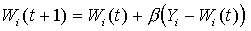
It is recommended to start c c on the order of one and gradually reduce to zero in the learning process. The iterative process will converge to a collective image obtained from a set of training vectors.

A feature of neurons in the form of Grossberg stars is the locality of memory. Each neuron in the form of an input star remembers "its" image relating to it and ignores the others. Each output star also has a specific command function. A memory image is associated with a specific neuron, and does not arise due to the interaction of multiple neurons in the network.

Winner Take All (WTA) Principle - Winner Takes It All - in the Lippmann-Hemming model.

Consider the problem of the belonging of an image x to a certain class X _k defined by given library images x _k . Each of the specified images of the training set directly defines its own class, and thus, the task is reduced to finding the "nearest" image. In the case of two binary (0-1) images, the distance between them can be determined by Hamming, as the number of mismatched components. Now after calculating all pairwise distances 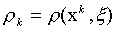The required class is determined by the smallest of them.

A neural network solution to this problem can be obtained on the basis of the Lippmann-Hemming architecture (Lippman R., 1987). The network has one layer of identical neurons, the number of which is equal to the number of classes. Thus, each neuron is "responsible" for its class. Each neuron is associated with each of the inputs, the number of which is equal to the dimensions of the considered library images. The weights of connections are assumed to be equal to the normalized library images:

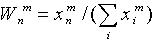
Here 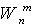- the value of the connection weight from the n-th input to the m-th neuron (see fig. 7.1.). The process of receipt of information about the vector x in the neural network is non-iterative. In this case, the input vector is first normalized:

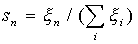
and neurons accept initial activity levels:

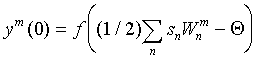
Here f (x) is the transition function (activation function) of the neuron, which is chosen to be zero for x <0, and f (x) = x for x> 0. The thresholds Q are usually set to zero.

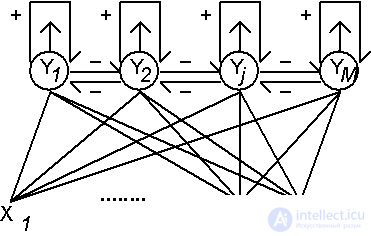
Fig. 7.1. Neural network of Lippmann-Hemming.

Upon receipt of the input vector, the initial excitation is obtained by all neurons, the scalar product of memory vectors with the input vector exceeds the threshold. In the future, among them to choose one for which it is the maximum. This is achieved by introducing additional feedbacks between neurons, arranged according to the principle of "lateral inhibition". Each neuron receives an inhibitory (negative) effect from all other neurons, in proportion to the degree of their excitation, and experiences an exciting (positive) effect on itself. The weights of the lateral connections in the neural layer are normalized in such a way that the total signal is exciting only for the neuron with the maximum initial activity. The rest of the neurons are inhibited:

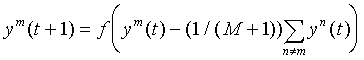
After performing a certain number of iterations t for all but one of the neurons, the value of the argument of the function f (x) becomes negative, which makes their activity ym zero. The only remaining active neuron is the winner. He points to the class to which the entered image belongs. This mechanism was named Winner Take All (Winner Take All - WTA). The WTA mechanism is also used in other neural network architectures. The principle of lateral inhibition laid in its basis has deep biological bases and is very widespread in neural networks of living organisms.

The Lippmann-Hemming neural network paradigm is a model with a direct memory structure. The information contained in the library images is not generalized at all, but is directly remembered in synaptic connections. The memory here is not distributed, since if one neuron fails, information about the entire memory image corresponding to it is completely lost.

Kohonen self-organization map.

In contrast to the Hamming network, the Kohonen model (T.Kohonen, 1982) performs a generalization of the provided information. As a result of the work of the NA Kohonen, an image is obtained that represents a map of the distribution of vectors from the training set. Thus, in the Kohonen model, the problem of finding clusters in the space of input images is solved.

This network is trained without a teacher on the basis of self-organization. As the vector of weights is trained, neurons tend to cluster centers — groups of vectors of the training sample. At the stage of solving information problems, the network assigns a new proclaimed image to one of the formed clusters, thereby indicating the category to which it belongs.

Consider the architecture of the National Assembly Kohonen and the rules of learning in more detail. The Kohonen network, as well as the Lippmann-Hemming network, consists of a single layer of neurons. The number of inputs of each neuron is equal to the dimension of the input image. The number of neurons is determined by the degree of detail with which you want to cluster the set of library images. With a sufficient number of neurons and successful training parameters, the Kohonen National Assembly can not only single out the main groups of images, but also establish the “fine structure” of the obtained clusters. At the same time, close neural activity maps will correspond to the close input images.

Fig. 7.2. An example of the map Kohonen. The size of each square corresponds to the degree of excitation of the corresponding neuron.

Learning begins with assigning random values ​​to a relationship matrix. 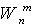. In the future, there is a process of self-organization, consisting in modifying the weights when presenting the vectors of the training sample to the input. For each neuron, you can determine its distance to the input vector:

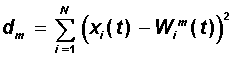
Next, choose a neuron m = m ^* , for which this distance is minimal. At the current learning step t, only the neuron weights from the neuron vicinity m ^* will be modified:

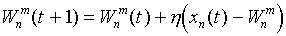
Initially, all the neurons of the network are located in the vicinity of any of the neurons, and later this neighborhood is narrowed. At the end of the learning phase, only the weights of the nearest neuron are adjusted. The learning rate h (t) <1 also decreases over time. The images of the training sample are pre'a consistent, and each time the scales are adjusted. Kohonen's neural network can be trained on distorted versions of the input vectors, in the process of learning distortions, if they are not systematic, are smoothed out.

For clarity, the presentation of the map Kohonen neurons can be arranged in a two-dimensional matrix, while under the neighborhood of the winner's neuron are taken adjacent (in rows and columns) matrix elements. It is convenient to present the resulting map in the form of a two-dimensional image, in which different degrees of excitation of all neurons are displayed as squares of various areas. An example of a map constructed from 100 Kohonen neurons is shown in Fig.7.2.

Each neuron carries information about a cluster - a bunch in the space of input images, forming a collective image for this group. Thus, the Kohonen National Assembly is capable of generalization. Several neurons with similar values ​​of the weights vectors can correspond to a particular cluster, therefore the failure of one neuron is not so critical for the functioning of the Kohonen National Assembly, as was the case with the Hamming network.

Neural network of counter distribution.

The counter propagation architecture successfully combines the advantages of the possibility of summarizing the Kohonen network information and the simplicity of learning the output Grossberg star. R.Hecht-Nielsen (R.Hecht-Nielsen, 1987), the creator of the counterpropagation network, recommends using this architecture to quickly model systems in the initial stages of research with a further transition, if necessary, to a much more expensive, but more accurate, method of learning with reverse error propagation.

A counterpropagation NA (BP) is trained on sampling vector pairs (X, Y) a of representing the X ® Y map. A remarkable feature of this network is the ability to also learn how to map the XY population to itself. At the same time, due to the generalization, it becomes possible to reconstruct the pair (XY) by one known component (X or Y). At the appearance at the stage of recognizing only the vector X (with zero initial Y), a direct mapping is performed - Y is restored, and vice versa, with the known Y, the corresponding X can be restored. The ability to solve both the direct and inverse problems, as well as the hybrid problem to restore the individual missing components makes this neural network architecture a unique tool.

The BP network consists of two layers of neurons (see Fig.7.3.) - the Kohonen layer and the Grossberg layer. In the mode of functioning (recognition), the Kohonen layer neurons work on the principle Winner-Take-All, determining the cluster to which the input image belongs. Then, the output star of the Grossberg layer on the signal of the winning neuron in the Kohonen layer reproduces the corresponding image at the network outputs.

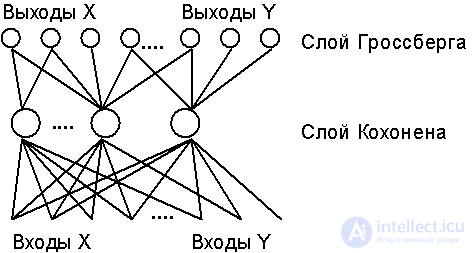
Fig. 7.3. The network architecture of counter-distribution (to simplify the image, not all links are shown).

Training of Kohonen layer weights is performed without a teacher on the basis of self-organization (see the previous paragraph). The input vector (analog) is first normalized, keeping the direction. After performing one iteration of learning, the neuron is determined the winner, its state of excitation is set to unity, and the weights of the corresponding Grossberg star can now be modified. The learning rates of the Kohonen and Grossberg neurons should be consistent. In the Kohonen layer, the weights of all neurons in the victor's vicinity are trained, which gradually narrows to one neuron.

The trained neural network of the BP can also function in the interpolation mode, when several winners are left in the Kohonen layer. Then their activity levels are proportionally normalized to total one, and the output vector is determined by the sum of the output vectors of each of the active Grossberg stars. Thus, the NN performs linear interpolation between the values ​​of the output vectors corresponding to several clusters. However, the interpolation mode in the counterpropagation network has not been studied enough to recommend its widespread use.