Lecture
Learning neural networks with examples. Formation of generalizations (categories) during training. Characteristic and configuration (phase) space of a neural network. Learning as a multifactor optimization task.
According to its organization and functionality, an artificial neural network with several inputs and outputs performs some transformation of input stimuli — sensory information about the outside world — into output control signals. The number of stimuli to be converted is n - the number of network inputs, and the number of output signals corresponds to the number of outputs m. The collection of all possible input vectors of dimension n forms a vector space X , which we will call feature space (Considering the corresponding spaces, it is assumed to use the usual vector operations of addition and multiplication by a scalar (see Lecture 2 for more details.) Similarly, output vectors also form a feature space, which . Y is denoted Now the neural network can be thought of as a multidimensional function F: X ® Y, the argument attribute space belongs moves, and the value - output attribute space.
With an arbitrary value of the synaptic weights of the neurons of the network, the function implemented by the network is also arbitrary. To obtain the required function, a specific choice of weights is required . An ordered set of all weights of all neurons can be represented as a vector W. The set of all such vectors also forms a vector space, called the state space or the configuration (phase) space W. The term "phase space" comes from the statistical physics of many-particle systems, where it is understood as the set of coordinates and momenta of all the particles that make up the system.
The assignment of a vector in the configuration space fully defines all synaptic weights and, thus, the state of the network. The state in which the neural network performs the required function is called the trained state of the network W * . Note that for a given function, the trained state may not exist or be not the only one. The learning task is now formally equivalent to constructing the process of transition in the configuration space from some arbitrary state W 0 to the trained state.
The required function is unambiguously described by specifying the correspondence to each vector of the feature space X of a certain vector from the space Y. In the case of a network of one neuron in the problem of border detection, considered at the end of the third Lecture, a full description of the required function is achieved by setting only four pairs of vectors. However, in the general case, such as when working with a video image, feature spaces can have a high dimension, therefore even in the case of Boolean vectors, the unique definition of a function becomes quite cumbersome (assuming, of course, if the function is not explicitly specified, for example, by the formula; however, for explicitly defined functions usually do not arise the need to represent them by neural network models). In many practical cases, the values of the required functions for given values of the argument are obtained from experiment or observation, and, therefore, are known only for a limited set of vectors. In addition, the known values of the function may contain errors, and some data may even partially contradict each other. For these reasons, the neural network is usually tasked with approximating the function representation by the available examples . The researcher’s available examples of correspondences between vectors, or the most representative data selected from all the examples are called the training set . A training sample is usually determined by specifying pairs of vectors, and in each pair, one vector corresponds to the stimulus, and the second one corresponds to the desired response. Training of the neural network consists in bringing all the vectors of stimuli from the training sample to the required reactions by choosing the weights of the neurons.
The general problem of cybernetics, which consists in building an artificial system with a given functional behavior, in the context of neural networks is understood as the task of synthesizing the required artificial network. It may include the following subtasks: 1) the selection of essential features for the problem being solved and the formation of feature spaces; 2) the choice or development of the neural network architecture adequate to the problem to be solved; 3) obtaining a training sample from the most representative, in the expert's opinion, vectors of feature spaces; 4) training of the neural network on the training set.
Note that subtasks 1) -3) largely require expert experience in working with neural networks, and there are no comprehensive formal recommendations. These questions are considered throughout the book as applied to various neural network architectures, with illustrations of the features of their learning and application.
In the case when the output attribute space is a discrete list of two or more data groups, the task of the neural network is to assign the input vectors to one of these groups. In this case, it is said that the neural network system performs data classification or categorization .
These two intellectual tasks, apparently, should be distinguished from each other. The term class can be defined as a set of objects or concepts (images), selected and grouped according to certain characteristics or rules. By classification we shall mean the assignment of a certain image to a class, performed according to these formal rules by a combination of features. The category (apart from the specific philosophical nature of this concept) defines only some general properties of the images and the connections between them. The categorization task, i.e. determining the relationship of this image to a certain category is much less defined than the task of the relationship to the class. The boundaries of various categories are fuzzy, vague, and usually the category itself is understood not through a formal definition, but only in comparison with other categories. The boundaries of classes, on the contrary, are determined quite accurately - the image belongs to this class, if it is known that it possesses the necessary number of features characteristic of this class.
So, the task of classifier systems is to establish the belonging of an image to one of the formally defined classes. Examples of such a task are the task of classifying plants in botany, the classification of chemicals by their properties and the types of possible reactions into which they enter, and others. Formal attributes can be defined by means of the rules “if ..- then ..”, and the systems operating with such rules are called expert systems . The traditional field of application of classifiers on neural networks is experimental high-energy physics, where one of the urgent problems is the selection among the set of events recorded in the experiment with elementary particles of events of interest for this experiment.
The problem of categorization is one step higher in complexity compared to classification. Its peculiarity lies in the fact that in addition to attributing the image to a group, it is required to determine these groups themselves, i.e. form categories.
In the case of training with a teacher (for example, in a perceptron), the formation of categories occurs through trial and error based on examples with known answers provided by an expert. The formation of categories is very similar to the learning process in living organisms, therefore, usually an expert is called a “supervisor” or teacher. The teacher manages the training by changing the connection parameters and, less commonly, the network topology itself.
The task of the categorizer is the formation of generalizing features in a combination of examples. With an increase in the number of examples, irrelevant, random signs are smoothed out, and often occurring ones are amplified, with a gradual refinement of the category boundaries. A well-trained neural network system is capable of extracting features from new examples previously unknown to the system, and making acceptable decisions based on them.
It is important to note the difference in the nature of the implicit "knowledge" memorized by the artificial neural network, and the explicit, formal "knowledge" embodied in expert systems. Some of the similarities and differences are presented in the following table.
| Expert Systems (ES) | Neural Network Systems (NS) | |
| Source of knowledge | Formalized expert experience, expressed in the form of logical statements - rules and facts, unconditionally accepted by the system | Cumulative experience of an expert-teacher who selects examples for training + individual experience of a neural network that learns from these examples |
| Nature of knowledge | Formal logical "left-hemisphere" knowledge in the form of rules | Associative "hemispheric" knowledge in the form of connections between neurons of the network |
| Knowledge development | In the form of expanding the set of rules and facts (knowledge base) | In the form of additional training on an additional sequence of examples, specifying the boundaries of categories and the formation of new categories |
Expert role | Sets based on the rules the full amount of knowledge of the expert system | Select specific examples without specifically formulating the rationale for your choice. |
| The role of the artificial system | Search the chain of facts and rules to prove judgment | Formation of individual experience in the form of categories derived from examples and categorization of images |
Differences in the nature of expert and neural network systems determine the differences in their fields of application. Expert systems are applied in narrow subject areas with well-structured knowledge, such as classification of faults of a particular type of equipment, pharmacology, analysis of chemical composition of samples, etc. Neural networks are used in addition to the listed areas and in tasks with poorly structured information, for example, in pattern recognition, handwriting, speech analysis, etc.
The possibility of applying the theory of optimization and training of neural networks is extremely attractive, since there are many well-tested optimization methods brought to standard computer programs. Comparison of the learning process with the process of finding some optimum is also not without biological grounds, if we consider the elements of the organism's adaptation to environmental conditions in the form of an optimal amount of food, optimal energy expenditure, etc. A detailed consideration of optimization methods is beyond the scope of these lectures, so here we are limited to only basic concepts. For a more detailed acquaintance, we can recommend the book by B. Bandi.
The function of one real variable f (x) reaches a local minimum at some point x 0 if there is a d- neighborhood of this point such that for all x from this neighborhood, i.e. such that | x - x 0 | < d , f (x)> f (x 0 ) holds.
Without additional assumptions about the smoothness properties of a function, it is impossible to find out whether a certain point is a reliable minimum point using this definition, since any neighborhood contains a continuum of points. When applying numerical methods for an approximate search for a minimum, the researcher may encounter several problems. First, the function minimum may not be the only one. Secondly, in practice, it is often necessary to find a global , rather than a local minimum, but it is usually not clear whether the function has another, deeper than the one found, a minimum.
The mathematical definition of a local minimum of a function in a multidimensional space has the same form if we replace the points x and x 0 by vectors and use the norm instead of the module. Finding a minimum for a function of many variables (many factors ) is significantly more difficult than for a single variable. This is primarily due to the fact that the local direction of reducing the value of the function may not correspond to the movement of the movement to the minimum point. In addition, as the dimension grows, the cost of calculating a function quickly increases.
The solution of the optimization problem is in many ways an art, there are no general, obviously working and effective methods in any situation. Among the frequently used methods we can recommend the Nelder simplex method, some gradient methods, as well as random search methods. In Appendix 2, in order to solve the optimization problem, the methods of simulating annealing and genetic search are related to the family of random search methods.
If the independent variables are discrete and can take one value from some fixed set, the multidimensional optimization problem is somewhat simplified. In this case, the set of search points becomes finite , and therefore the problem can be, at least in principle, solved by a full brute force method. We will call optimization problems with a finite set of search problems of combinatorial optimization .
For combinatorial problems, there are also methods for finding an approximate solution, offering some sorting strategy for points, reducing the amount of computational work. Note that the simulated annealing and the genetic algorithm are also applicable to combinatorial optimization.
Let there be a neural network that transforms F: X ® Y vectors X from the attribute space of inputs X into vectors Y of the output space Y. The network is in the W state from the W state space. Suppose further that there is a training sample (X a , Y a ), a = 1..p. Consider the total error E made by the network in the W state.
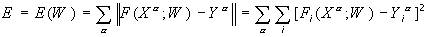
Note the two properties of the complete error. First, the error E = E (W) is a function of the state W defined on the state space. By definition, it takes non-negative values. Secondly, in some trained state W * , in which the network does not make mistakes on the training set, this function takes a zero value. Consequently, the trained states are the minimum points of the introduced function E (W).
Thus, the task of teaching a neural network is the task of finding the minimum of the error function in the state space, and, therefore, standard methods of optimization theory can be used to solve it. This task belongs to the class of multi-factor problems, for example, for a single-layer perceptron with N inputs and M outputs, it is about finding a minimum in NxM-dimensional space.
In practice, neural networks can be used in states with some small error value that are not exactly the minima of the error function. In other words, a state is taken as a decision from the neighborhood of the trained state W * . At the same time, the permissible level of error is determined by the peculiarities of a specific application, as well as the amount of training costs acceptable to the user.
Synaptic weights of a single-layer perceptron with two inputs and one output can take values of -1 or 1. The threshold value is zero. Consider the task of teaching such a perceptron of the logical function “and” as a problem of multifactorial combinatorial optimization. For the training set use all combinations of binary inputs.
Comments
To leave a comment
Computational Neuroscience (Theory of Neuroscience) Theory and Applications of Artificial Neural Networks
Terms: Computational Neuroscience (Theory of Neuroscience) Theory and Applications of Artificial Neural Networks