Lecture
Это продолжение увлекательной статьи про схемотехника комбинационных узлов.
...
Компараторы – это КС, осуществляющие сравнение (от англ. Compare – сравнение) поступающих на их вход двоичных кодов. Результатом такого сравнения могут быть следующие значения выходного сигнала: „ А=В” (равенство кодов А и В ), „ А≠В” (неравенство кодов А и В ) и „ А<В” (код А меньше кода В ) или „ А>В” (код А больше кода В ), в случае „≠”.
Пусть заданы две совокупности переменных ν′=(x n , …, x p , …, x 1 ) и ν′′=(y n , …, y p , …, y 1 ). Так как x p =0 или 1 и y p =0 или 1, то каждая из совокупностей переменных ν′ и ν′′ имеет 2 n комбинаций значений. Для краткости такие совокупности значений переменных принято называть кодами, а величины x p и y p – разрядами кодов.
КС, реализующая функцию f(ν)=f(ν′, ν′′), где ν=( x n , …, x 1 , y n , …, y 1 ), которая равна 1 только при x p =y p для всех p=1…n, называется схемой равнозначности кодов . Разряды x p и y p равны только в том случае, если 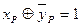 , поэтому функция
, поэтому функция 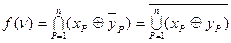 (здесь знак
(здесь знак 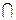 соответствует логической функции «И», а
соответствует логической функции «И», а 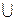 – функции «ИЛИ») принимает значение, равное 1, только при по - парном равенстве всех одноименных кодов. In fig.3.16, a and 3.16, b shows two schemes that implement the function f (ν), which are built for n = 4 on the basis of the expression obtained. The equivalence scheme is simplified when using an exclusive-OR LE with an open collector (Fig. 3.16, c)).
– функции «ИЛИ») принимает значение, равное 1, только при по - парном равенстве всех одноименных кодов. In fig.3.16, a and 3.16, b shows two schemes that implement the function f (ν), which are built for n = 4 on the basis of the expression obtained. The equivalence scheme is simplified when using an exclusive-OR LE with an open collector (Fig. 3.16, c)).
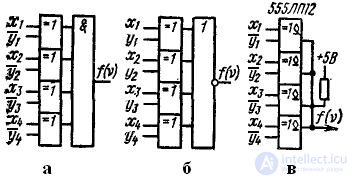
Fig. 3.16 Code Equivalency Schemes
Comparison schemes for binary numbers are devices that form, at their output, in addition to the signal of equality of input codes ( A = B ), also signals that carry information which of the input codes is greater than the other ( A and A> B ).
Let two n – bit numbers A = (x n , ..., x 1 ) and B = (y n , ..., y 1 ) be given, where x n and y n are the highest digits of these numbers. The relationship between the numbers A and B are described by five functions:

It is easy to notice that only two functions can be considered, for example, F ( A ) and F (A = B) , since other functions can be expressed through them.
To build a comparator with three outputs ( =,> and < ) for single-bit words (Table 3.8), it requires the implementation of functions: F A = B =  , F A > B =
, F A > B = 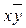 and F A < B =
and F A < B = 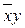 . The functional diagram of the comparator for single-bit words with three outputs is shown in Fig. 3.17.
. The functional diagram of the comparator for single-bit words with three outputs is shown in Fig. 3.17.
Tabl.3.8 truth table for comparator
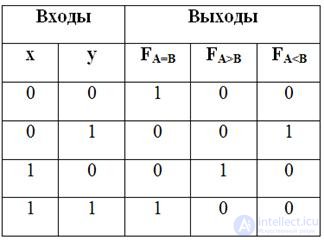
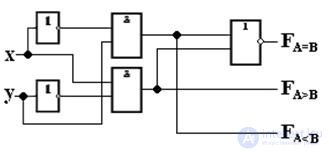
Fig.3.17 Functional diagram of the comparator for single-bit words
The function F A > B for multi-bit words can be obtained on the basis of reasoning, for example, when comparing two-digit words. If the high-order digits x i and y i are not equal, then the result is known regardless of the low-order digits: for x i = 1 and y i = 0, we have A> B , and for x i = 0 and y i = 1 we have A . If the high-order bits are equal ( x i = y i ), the result is unknown, and the analysis of the next bit is required by the same algorithm. Thus, for two-digit words you can write: 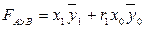 .
.
The reasoning for words of any digit capacity is similar - it is necessary to proceed to the analysis of the next digit only if the preceding ones are equal. For n-bit words:
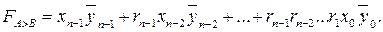 (3.12)
(3.12)
An example of the implementation of the comparator with three outputs for two-digit words is shown in Figure 3.18. The development of the sign A> B in this scheme is made according to the ratio of 3.13 (the corresponding outputs of the younger group comparator are indicated by a stroke):
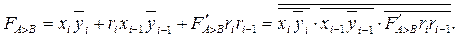 (3.13)
(3.13)
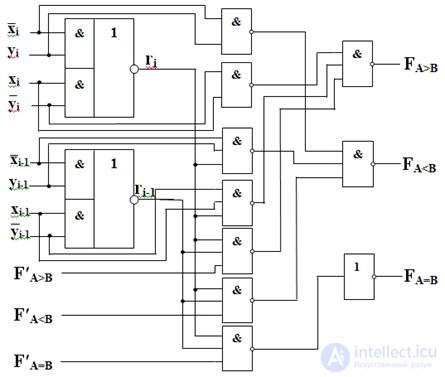
Fig.3.18 Comparator for two-digit words
In the series of digital elements are presented comparators with three outputs ( =,>, < ). Conditional graphic designation of such a comparator is shown in Figure 3.19.
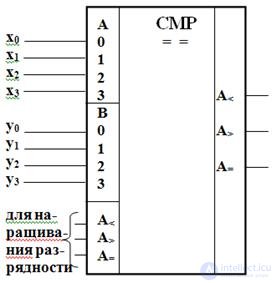
Fig. 3.19. Conditional graphic four-digit
comparator with three outputs
Figure 3.20 shows a cascade connection of comparators for comparing two eight-bit numbers. With this connection, the outputs A = B , A previous chip (low-order bits) are connected to the corresponding inputs of the subsequent one. The inputs A = B , A and A> B chips of the lower digits are supplied respectively with the signals U 0 , U 1 , U 1 ( U 0 corresponds to the level of the log "0", U 1 - log. "1"). In subsequent chips to the input A> B signal U 1 .
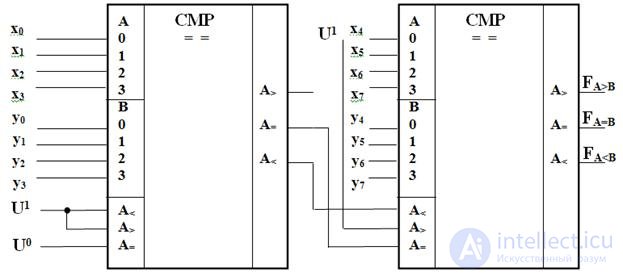
Fig. 3.20. Comparators cascade connection
Presented in Fig. 3.20 the cascading scheme of comparators has a significant drawback, which consists in increasing the signal propagation delay with an increase in the capacity of the compared codes. If only the fact of equality or inequality of input codes is important to us, then we can increase the speed when combining comparators by giving their output signals to the AND element (Fig. 3.21). In this case, the total delay of the circuit will exceed the delay of one comparator only by the delay of element I. When using comparators with inverse output, it is necessary to take the element OR with the required number of inputs.
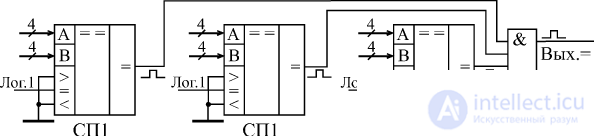
Fig. 3.21. Reducing compass cascading delay
Adder is an operational element of a computer, which is a circuit that performs arithmetic addition and subtraction of digital codes of two numbers.
According to the method of processing multi - digit numbers, adders can be sequential , parallel and parallel-serial .
Sequential adders are based on single-bit adders and are used to add consecutive binary codes. Parallel n -bit adder is built from n single-digit adders according to the cascade principle, while the processing of the summation of numbers is performed simultaneously in all digits. In this case, the design of a multi-digit adder is reduced to the synthesis of a single-digit adder and the organization of transfer chains between the digits in accordance with the requirements for speed.
After the time of summation T cm after the submission of the items, a multi-bit result is formed at the output of the adder. The summation time depends both on the average delay time of the signal propagation in the used logic elements T le , and on the organization of the transfer chains in the adder.
A single-digit full adder has three inputs (two terms and a transfer from the previous digit) and two outputs (a sum and transfer to the next digit). The truth table (Table 7.2.2) of the single-digit adder is:
| Value of binary numbers | Digit amount S i | Transfer to the next rank С i | ||
| a i | b i | with i-1 | ||
Logical dependencies (3.14), formed according to the truth table, are the canonical equations of the adder:

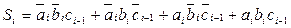 ;
;
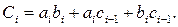
In the AND-NOT basis (Scheffer stroke), logical dependencies (3.14) have the form (3.15):
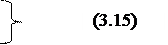
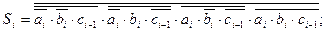
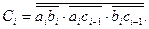
Direct reproduction of the obtained formulas on the elements of the two-stage AND-OR-NOT logic leads to the use of the element 2-2-2И-OR-NOT to generate the transfer signal 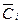 and item 3-3-3-3-AND-OR-NOT for a signal
and item 3-3-3-3-AND-OR-NOT for a signal 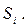 However, the best solution, leading to some reduction in the hardware complexity of the circuit while maintaining the minimum delay along the transfer chain, is obtained by using the obtained value
However, the best solution, leading to some reduction in the hardware complexity of the circuit while maintaining the minimum delay along the transfer chain, is obtained by using the obtained value 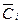 as an auxiliary argument when calculating
as an auxiliary argument when calculating 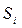 .
.
From table 3.9 it follows that in all lines, except the first and last, 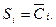 To make this formula valid for the first and last lines, you need to remove one in the line of zero input values and add one to the line of single input values. Such an operation leads to relation (3.16).
To make this formula valid for the first and last lines, you need to remove one in the line of zero input values and add one to the line of single input values. Such an operation leads to relation (3.16).
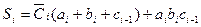 (3.16)
(3.16)
The circuit of the adder, constructed from the relation (3.16), is shown in Figure 3.22.
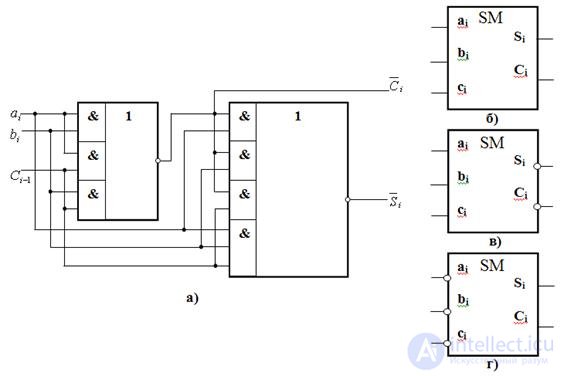
Fig. 3.22. Functional diagram (a) and conventional graphic symbols (b, c, d) of a full one-digit adder
To add two n- bit binary numbers A and B, you must use n-single-bit full adders. In this case, two ways of summation can be used - sequential and parallel. The use of one or another method of summation depends on the nature of the input / output of numbers and the organization of carries in a multi-digit adder.
The sequential adder (Fig. 3.23, a) summarizes the binary numbers arriving with a certain tact, bitwise, starting with the least significant digit, with the help of a full one-digit adder. The transfer of C i +1 formed in this discharge with the help of a delay circuit is delayed by one clock cycle following the digits and is fed to the input C i of the adder at the moment of arrival of the subsequent discharge. By adding the lower digits, the multi-digit adder produces the sum for the lower digit of the result and the transfer, which is delayed by one clock cycle. In the next cycle, the newly received digits of the terms a i and b i are added with transfer from the lower order, etc.
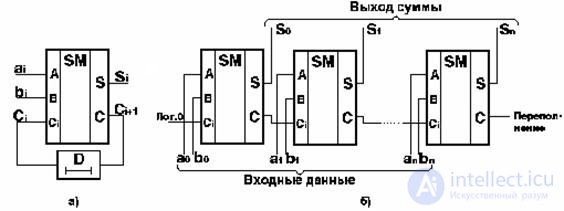
Fig. 3.23. Functional sequential (a) and parallel (b) adders
The parallel adder summarizes two multi-digit numbers simultaneously in all digits and is characterized by different ways of transferring carries from lower digits to older ones. The scheme of functioning of a multi-bit parallel combinational adder is composed of one-bit and has the form shown in Figure 3.23, b. Summation in all digits, starting with the youngest, occurs according to the same rules. In each i-th digit is the addition of a i + b i + c i -1 . The result is represented by the codes of the sum S i and the transfer C i .
To increase the performance of multi-digit adders, obtained by the sequential inclusion of single-digit adders, it is necessary to reduce the propagation time of the transfer signal from input to output.
Due to the great complexity of creating parallel adders for n-digits, they are almost never used in their pure form. However, the principle of parallel transfer is used in adders with group (parallel-sequential) transfer . The principle of which is explained as follows:
From (3.14) follows 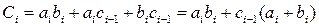 , or
, or 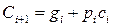 , if in this expression to accept that
, if in this expression to accept that 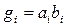 , but
, but 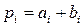 . In this case, for a 4-bit adder, the transfer output function from the highest (fourth) digit will be as follows:
. In this case, for a 4-bit adder, the transfer output function from the highest (fourth) digit will be as follows:
|
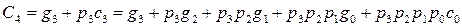 .
.
If the internal hyphenation in such an adder is implemented by logic functioning in accordance with (3.17), then such an adder is called a parallel-transfer adder, unlike a sequential transfer adder, the block diagram of which is shown in
rice 3.23, b.
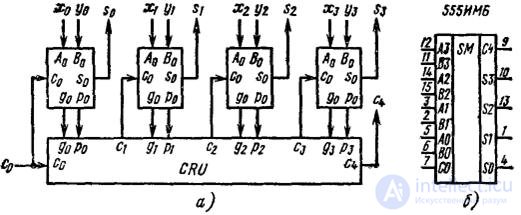
Fig. 3.24 Block diagram of a four-bit parallel adder with a parallel transfer formation circuit (a) and IC 555IM6 with output numbering (b)
In fig. 3.24, and the block diagram of a 4-digit parallel transfer adder is presented, where CRU is the Carry Unit (transfer device). In fig. 3.24, b shows the graphic designation of the 555IM6 transfer chip.
Thus, a parallel adder with group transfer is formed from an n-bit adder, has N groups, within the boundaries of each of which the formation of transfer is carried out simultaneously, without delay from discharge to discharge. The transfer output from the junior group of digits is one of the components for the formation of a transfer signal to the next senior group. Those. the transfer formation delay at the output of the adder will be determined by the total transfer formation delay in the N groups. In comparison with a conventional adder, a faster response is achieved in a group transfer adder.
The adder can calculate not only the sum, but also the difference between the input codes, that is, to work as a subtractor . To do this, the subtracted number needs to be simply inverted in bits, and a single signal should be sent to the transfer input C (Fig. 3.25).
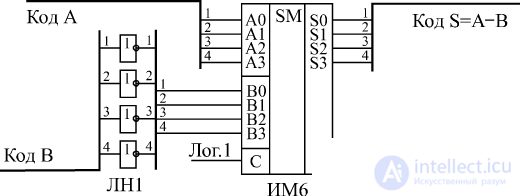
Fig. 3.25 4-bit subtractor on the IM6 adder and LN1 inverters
To perform on the operands A and B both arithmetic and logical operations are used universal arithmetic logic chips (ALU) chips. The basis of the ALU is the adder, the circuit of which is supplemented with logic that extends the functionality of the ALU and ensures its restructuring from one operation to another.
Most often, the ALUs are four-digit, and to increase the digit capacity they are combined with the formation of sequential or parallel transfers. The logical capabilities of the ALU of different technologies (TTLSH, CMOS, ECL) are similar.
Depending on the construction and nature of the work, they distinguish ALUs of sequential, parallel and parallel - of sequential action. In an ALU sequential operation, operations on codes are carried out sequentially, discharge by discharge. The code of a number is represented as a series of signals acting in the same circuit at different points in time. In the ALU parallel operation operations on the codes of numbers are carried out in parallel for all digits. The codes of numbers are depicted as a set of signals, each of which acts along its own specific chain. Such ALU received the most widespread use. In the ALU in parallel - sequential action codes of numbers are divided into groups of a certain number of digits. Operations on the codes of numbers within each group are carried out in parallel, and operations between groups of digits are performed sequentially.
Figure 3.26 shows the conditional graphic designation of the ALU. Here A and B are the inputs of the operands, S are the inputs of the choice of operations, C i is the transfer signal and M (Mode) is the operation type setting signal: M = 1 corresponds to logical operations, and M = 0 to arithmetic. The result of the operation is given to the outputs Y , the outputs G and H are intended for issuing the generation and transparency values used for organizing parallel transfers when increasing the dimension of the ALU. The signal C o is the transfer output, and the output A = B <> is the comparison output for equality with the open collector.
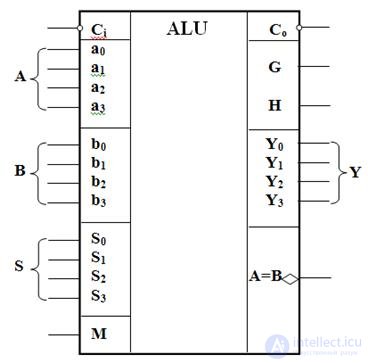
Fig.3.26 Conditional graphic designation of ALU
Table 3.10 lists the operations performed by the ALU. Sixteen logical operations allow you to play all the functions of two variables. In arithmetic-logical operations, there are operations that are both logical and arithmetic at the same time.
Record 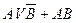 means: first inverting operations are performed (
means: first inverting operations are performed ( 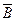 ), followed by logical addition (
), followed by logical addition ( 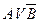 ) and multiplications (
) and multiplications ( 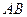 ), and then the results (
), and then the results ( 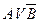 ) and (
) and ( 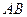 ) add up arithmetically.
) add up arithmetically.
During operations on words of large dimension, the ALU are connected to each other with the organization of sequential or parallel translations. In the latter case, microcircuits are used in conjunction with the ALU: accelerated transfer units (CRUs), which receive generation and transparency signals from individual ALUs, as well as input transfer and generate transfer signals.
Possible block and multifunctional structure of the ALU. A block ALU contains a set of devices for performing certain types of operations or operations on certain types of operands. In the multifunctional ALU, all operations on any numbers are performed in one device. The basis of such an ALU is formed by adders and registers which, when performing individual operations, are switched among themselves in a certain way by means of groups of logical elements. ALU block type consist of separate blocks of addition, multiplication, division, etc. Such ALUs are faster than multi-functional ones, but they require more equipment for their implementation.
Table 3.10 List of operations performed by the ALU
| S 3 | S 2 | S 1 | S 0 | Logical functions (M = 1) | Arithmetic logic functions (M = 0) |
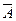 |
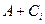 |
||||
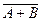 |
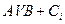 |
||||
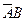 |
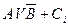 |
||||
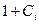 |
|||||
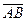 |
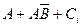 |
||||
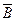 |
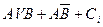 |
||||
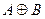 |
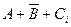 |
||||
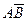 |
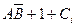 |
||||
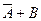 |
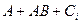 |
||||
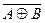 |
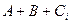 |
||||
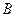 |
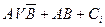 |
||||
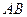 |
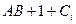 |
||||
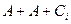 |
|||||
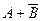 |
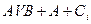 |
||||
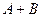 |
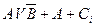 |
||||
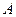 |
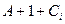 |
Chips for multiplying devices appeared in the 80s of the 20th century, when the achieved level of integration allowed to place a sufficiently large number of logical elements in a single chip.
The structure of matrix multipliers is closely related to the structure of mathematical expressions describing the multiplication operation.
Пусть имеются два целых двоичных числа без знаков A m =a m -1 …a 0 и B n =b n -1 …b 0 . Их перемножение выполняется по известной схеме «умножения столбиком». Если числа четырехразрядные, т.е. m=n=4, то
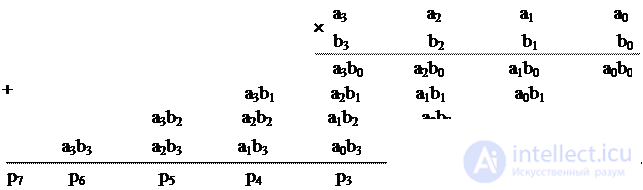 |
Произведение выражается числом P m + n -1 =p m + n -1 p m + n -2 … p 0 . Члены a i b j , где i=0… (m-1) и j=0… (n-1) вырабатываются параллельно во времени конъюнкторами. Их сложение в столбцах, которое можно выполнять разными способами, составляет основную операцию для умножителя и определяет почти целиком время перемножения.
Матричные перемножители могут быть просто множительными блоками (МБ) или множительно-суммирующими (МСБ), при этом последние обеспечивают удобство наращивания размерности умножителя.
МСБ реализуют операцию P=A m ×B n + C m ×D n , т.е. добавляют к произведению два слагаемых: одно разрядности m , совпадающего с разрядностью множимого, другое разрядности n , совпадающей с разрядностью множителя.
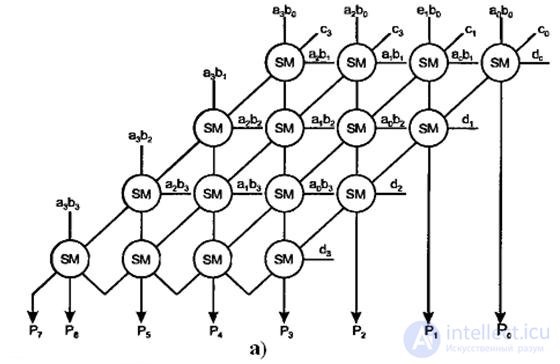
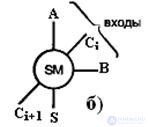
Рис.3.27 Схема множительно-суммирующего блока для четырёхразрядных сомножителей (а), обозначение одноразрядного сумматора для данной схемы
Множительно-суммирующий блок для четырехразрядных операндов без набора конъюнкторов, вырабатывающих члены вида a i b j , показан на
rice 3.27,а, где для одноразрядного сумматора принято обозначение
(рис. 3.27,б).
Максимальная длительность умножения – сумма задержек сигналов в конъюнкторах для выработки членов a i b j и задержки в наиболее длинной цепочке передачи сигнала в матрице одноразрядных сумматоров, равной 2n-1 ( m+n-1 в общем случае). Таким образом, t МСБ =t K +(2n-1)t SM .
Построение умножителей большей размерности из умножителей меньшей размерности на основе МСБ предполагает нахождение частичных произведений и дальнейшее их сложение с учётом взаимного положения (сдвига одного относительно другого).
В задачу синтеза любых цифровых схем, в том числе и комбинационных, входит построение принципиальной схемы устройства, реализующего заданные условия его работы с учетом заданного базиса элементов. Задание комбинационного узла сводится к заданию тех функций, которые он должен реализовать. Число функций определяется только числом выходов разрабатываемого комбинационного узла.
Процесс синтеза КУ состоит из 2-х этапов:
1. Абстрактный синтез , который включает:
Ø формирование задачи, словесное описание функций устройства, определение типа устройства;
Ø описание устройства на формализованных языках: таблица истинности, карта Карно, аналитическое выражение и т.д.;
Ø минимизация булевых функций;
Ø построение логической схемы устройства.
2. Схемный синтез , в процессе которого осуществляется:
Ø переход в требуемый базис;
Ø построение принципиальной схемы;
Ø разработка монтажной схемы;
Ø изготовление устройства и его испытания.
По завершении испытаний и анализа их результатов может потребоваться корректировка схемы. Завершается синтез подготовкой технической документации.
В практике проектирования ЭВМ накоплен огромный опыт по синтезу различных схем. Общая постановка задачи структурного синтеза комбинационных схем (КС) заключается в построении оптимального проектируемого устройства, моделирующего закон функционирования цифрового устройства без памяти, представленного одной булевой функцией или системой булевых функций.
Существует множество способов задания законов функционирования цифровых устройств комбинационного типа, но чаще всего для этого пользуются таблицами функционирования (таблицами истинности), задающими значения искомых функций на всех наборах входных аргументов. От таблицы истинности легко перейти к искомой функции в совершенной дизъюнктивной нормальной форме (СДНФ). Для этого составляется логическая сумма тех наборов аргументов, на которых функция принимает единичное значение. Например, для подлежащей воспроизведению функции четырех аргументов, заданной в табл. 3.11, получим:
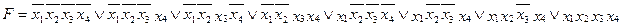
Таблица 3.11 Таблица истинности функции четырёх переменных
| x 1 | x 2 | x 3 | x 4 | F | x 1 | x 2 | x 3 | x 4 | F |
Дальнейшие действия зависят от средств реализации функций, к которым в современной схемотехнике относятся:
- логические блоки, собираемые из логических элементов некоторого базиса;
- универсальные логические блоки на основе мультиплексоров;
- логические блоки табличного типа;
- логические блоки в виде последовательности матриц элементов И и ИЛИ.
Синтез КС на логических блоках является самым традиционным и изученным. В этом случае абстрактный синтез КС содержит следующие этапы:
- минимизация логических функций;
- переход к заданному логическому базису.
Минимизация – это такое преобразование логических функций, которое упрощает их в смысле заданного критерия . Исторически первым критерием было стремление минимизировать число логических элементов в схеме (элементы были наиболее дорогими компонентами), что приводит к критерию сложности схемы в виде числа букв в реализуемых выражениях. Для минимизации по этому критерию разработано несколько методов, в их числе как аналитические, основанные на преобразованиях математических выражений, так и графические, основанные на применении специальных карт (карты Карно, диаграммы Вейча), удобных в использовании, если число аргументов функции не превышает 6.
Переход к заданному логическому базису от исходных выражений, которые получают в булевом базисе И, ИЛИ, НЕ, основан на применении закона двойственности (дуальности, теоремы де-Моргана).
К примеру, для перехода к базису И-НЕ функции 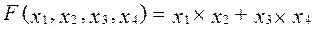 необходимо выполнить следующее преобразования:
необходимо выполнить следующее преобразования: 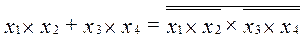 . Как видим, в исходном представлении функции присутствовали как конъюнкции
. Как видим, в исходном представлении функции присутствовали как конъюнкции 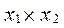 and
and 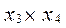 , так и их дизъюнкция. В преобразованном выражении присутствуют только конъюнкции с инверсиями. Это означает, что для реализации не преобразованной функции потребуются 2 логических элемента «И» и 1 «ИЛИ», а для преобразованной – 3 ЛЭ «И-НЕ».
, так и их дизъюнкция. В преобразованном выражении присутствуют только конъюнкции с инверсиями. Это означает, что для реализации не преобразованной функции потребуются 2 логических элемента «И» и 1 «ИЛИ», а для преобразованной – 3 ЛЭ «И-НЕ».
Различные методы выполнения абстрактного синтеза КС на базе логических блоков и на основе мультиплексоров были использованы ранее в этом разделе при рассмотрении наиболее распространённых комбинационных узлов, выпускаемых в виде микросхем – шифраторов, компараторов, мультиплексоров и т.д.
Для синтеза КС на основе логических блоков табличного типа обязательно необходимо чтобы функция была представлена в СДНФ. Дело в том, что табличный блок представляет собою память, в которой имеется столько ячеек, сколько необходимо для хранения всех значений функций, т.е. 2 m , где m – число аргументов функций. При этом, набор аргументов является адресом той ячейки, в которой хранится значение функции на данной наборе (0 или 1). СДНФ как раз и содержит все адреса, по которым нужно хранить единичные значения функции. Если функция выражена в какой-либо сокращенной форме, то следует перевести ее в СДНФ. Для этого конъюнктивные члены, не содержащие переменной 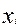 , умножаются на равную единице дизъюнкцию
, умножаются на равную единице дизъюнкцию 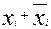 . К примеру, функция вида
. К примеру, функция вида 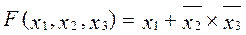 после умножения
после умножения 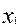 on
on 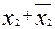 and
and 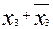 , but
, but 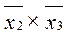 on
on 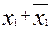 примет вид:
примет вид:
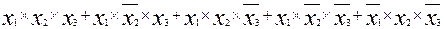 или, опустив знак конъюнкции -
или, опустив знак конъюнкции - 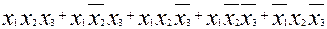 .
.
Блок памяти для воспроизведения функции m переменных имеет вид, представленный на рис. 3.28.а. Если требуется воспроизвести n функций, то в каждой ячейке нужно будет хранить бит (по одному биту для каждой функции), и блок памяти должен быть организован так, как показано на рис. 3.28.б.
Если размерность блоков табличного типа такова, что не позволяет получить искомую функцию с помощью одного блока, т.е. число входов блока памяти меньше числа аргументов функции, то появляется необходимость решения сложной задачи выражения искомой функции через подфункции с меньшим числом аргументов.
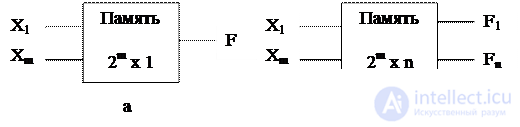
Fig. 3.28 Блоки памяти для воспроизведения одной (а) и нескольких (б) логических функций
В случае реализации проекта на логических блоках в виде последовательно включенных матриц элементов И и ИЛИ либо их эквивалентов в другом базисе, то исходную СДНФ можно минимизировать, если, конечно возникает такая необходимость. Логические блоки с матрицами И и ИЛИ воспроизводят системы переключательных функций и имеют параметры: число входов, выходов и термов. Число входов (аргументов воспроизводимых функций) и число выходов (самих функций) от формы выражения функций не зависят и предопределены заданием. Число термов (имеются в виду конъюнктивные термы) зависит от формы представления функций системы. Если число термов при данной форме представления функции превышает возможности логического блока, то возникает вопрос о минимизации функции. Целью минимизации будет сокращение числа конъюнктивных термов в данной системе функций, т.е. поиск кратчайших дизъюнктивных форм. Практически это сводится к поиску минимальных дизъюнктивных нормальных форм (МДНФ) и отбору среди них вариантов с достаточно малым числом термов. Как только находится форма с достаточно малым числом термов, поиск других форм можно прекратить, т.к. дальнейшее уменьшение числа термов системы эффекта не даст: сложность аппаратных средств воспроизведения системы не уменьшится. Разумеется, речь идет о реализации на уже выбранных средствах, а не о том, что могут быть применены иные логические блоки – того же типа, но иной размерности.
Из этапов с хемного синтеза комбинационных узлов далее более детально рассмотрим этап построения принципиальных схем , т.к. этап перехода в требуемый базис в зависимости от средств реализации функций, примененных при проведении абстрактного синтеза, уже либо выполнен в процессе абстрактного синтеза, либо вообще не требуется потому, что в качестве таких средств реализации выбраны ИС более высокой степени интеграции. Что касается разработки монтажной схемы, изготовления устройства и его испытания, то это вопросы, относящиеся к компетенции конструкторов и непосредственно изготовителей, поэтому в процессе освоения данной дисциплины рассматриваться не будут.
В первую очередь в процессе схемного синтеза на этапе разработки принципиальных схем необходимо обратить внимание на соблюдение выполнения следующих основных параметров используемых в проекте ИС.
Питающие напряжения ИС, которые, в случае применения в проекте различных серий, могут быть разными для выбранных ИС. С целью достижения минимальной стоимости проекта необходимо добиваться минимального количества питающих напряжений, либо принять необходимые меры, таких, как введение в принципиальную схему специальных электронных устройств, позволяющих получать из одного питающего напряжения (к примеру, +12 В), требуемых для функционирования всех ИС (к примеру, +6 В и 3.3 В).
Уровни логических сигналов для представления лог. «0» и лог. «1», в случае применения ИС разных серий. В данном случае речь идет об электрической совместимости цифровых схем, суть которой заключается в обеспечении согласованности полярности и уровней напряжений логического “0” и логической “1”.
Нагрузочная способность (коэффициент разветвления по выходу). Коэффициент разветвления по выходу (К раз ) показывает на какое количество логических входов может быть одновременно нагружен выход данного логического элемента. Обычно К раз для наиболее часто используемых серий равен 10. Иногда вместо К раз задается предельно допустимое значение выходного тока логического элемента в состоянии «0» или «1».
При построении КУ может оказаться, что выход k -го логического элемента нагружен n > К раз входов других ЛЭ (рис. 3.29,а). Это означает, что k -й логический элемент перегружен и необходимо принять меры, устраняющие указанное явление. Существуют два способа обеспечения заданного К раз :
· использование дополнительных развязывающих усилителей;
· дублирование перегруженного элемента.
Схема с использованием дополнительных развязывающих усилителей представлена на рис. 3.29,б. Количество p дополнительных усилителей, необходимых для обеспечения заданного К раз , определяется по формуле:
p > (n - К раз ) / (К раз - 1)
Недостаток рассматриваемого способа в том, что в цепь распространения сигнала вносится дополнительная задержка, что не всегда допустимо.
Схема с использованием дублирования перегружаемого элемента представлена на рис. 3.29,в. Количество p дополнительных элементов, выполняющих ту же функцию, что и k -й элемент, определяется по формуле: p > К раз .
При таком способе обеспечения К раз дополнительная задержка не вносится, но увеличивается нагрузка на элементы, формирующие сигналы 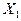 and
and 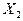 , что может привести к перегрузке этих элементов и введению дополнительных элементов для обеспечения заданного К раз .
, что может привести к перегрузке этих элементов и введению дополнительных элементов для обеспечения заданного К раз .
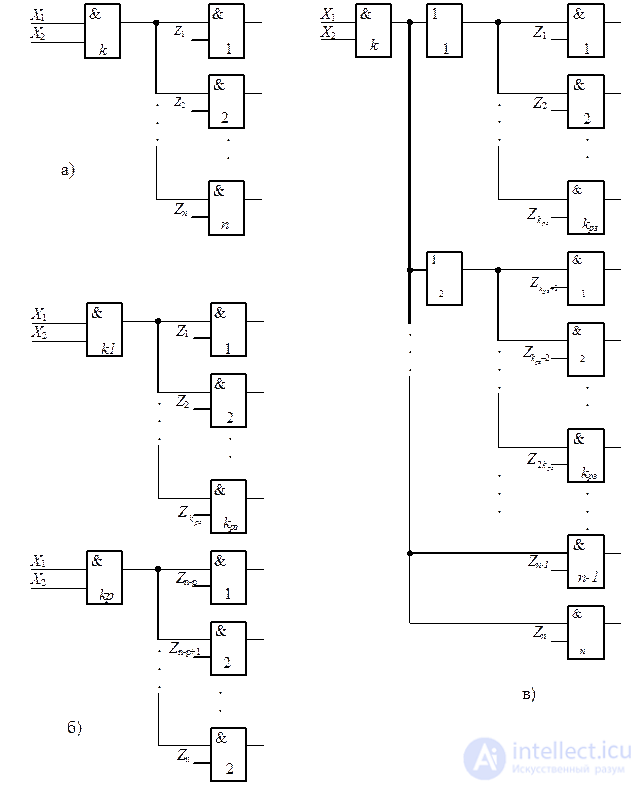 Fig. 3.29. Способы обеспечения требуемого К раз .
Fig. 3.29. Способы обеспечения требуемого К раз .
Коэффициент объединения по входу ( К об ) определяет максимально возможное число входов логического элемента, иными словами, функцию скольких переменных может реализовать этот элемент. Обычно К об принимает значение от 2 до 4, реже К об = 8. Увеличение числа входов связано с усложнением схемы элементов и приводит к ухудшению других параметров – помехоустойчивости, быстродействия и т.д.
Представлению функции в виде ДНФ соответствует двухуровневая КС (если считать, что на ее вход могут поступать как прямые так и инверсные входные сигналы), на первом уровне которой элементы И, а их выходы объединяются на втором уровне
продолжение следует...
Часть 1 Theme 3. Circuit design combinational nodes
Часть 2 3.7. Компараторы - Theme 3. Circuit design combinational nodes
Часть 3 3.11.2.5 Быстродействие - Theme 3. Circuit design combinational nodes
Comments
To leave a comment
Computer circuitry and computer architecture
Terms: Computer circuitry and computer architecture