Lecture
| The goal is to build a technical system that implements the learning and self-learning mechanism. The system must realize not a worse learning ability than a living creature. This requires exploring how living things are taught. | ||
Natural objects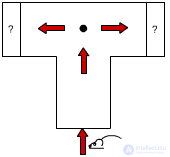
fig.3.1
Consider a T-shaped labyrinth (Figure 3.1). It starts up a little animal. In advance, she does not know what to expect in each side of the maze, food or electric shock (encouragement or punishment). The experience is repeated many times. First, there was always food on the right and a talk on the left. The little animal ran randomly only the first few times, then she trained and went to food. The experience was complicated: now food and punishment were in both parts of the labyrinth, but they were selected with a certain constant probability. On the right is P = 0.4, on the left - 0.9, where P is the probability of a penalty. Instead of a deterministic environment, the little animal fell into a probabilistic deterministic environment. As a result of the experiment, the little creature went to the right - it captured how to act rationally in new conditions. Then it was placed probabilistic non-deterministic environment, i.e. The probability of a fine began to change over time. |
||
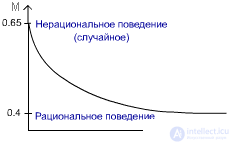
fig.3.2
For irrational behavior is characterized by the fact that the choice of direction is random. With equal probabilities, the animal can escape both right and left: M = 0.5 * 0.9 + 0.5 * 0.4 = 0.65 For rational behavior: M = 0 * 0.9 + 1 * 0.4 = 0.4 The ability to learn can be measured by rationality of behavior. E = (P l , P p ) , where E is the medium, Pl, Pn are the probabilities of the punishment by the medium under the actions d1, d2, respectively. In our case, d1 - go left, d2 - go right. The environment is two-component, because only two actions are possible. |
||
Linear tactic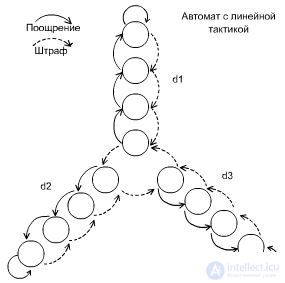
fig.3.3
The automaton implements three actions d1, d2, d3. Three-component environment. Let the medium behave as follows: E = (0.9, 0.0001, 0.8) . If the environment is fined, then we emerge (from the depth of the petal), if it encourages, then we go deep into the petal. Let the initial state of the automaton be one of the states in the petal d1. Because the probability of a fine here is quite large (0.9), then after a while the machine will go into a state located in d3 and will remain there for a long time. That is, the automaton behaves well in a previously unknown environment. |
||
Trusting Machine (Krinsky Machine)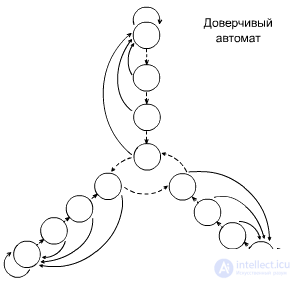
fig.3.4
Introduced a nuance of temperament. Acts the same as the previous one. |
||
Krylov's careful machineA machine with a linear tactic, but with rewards it trusts not immediately, but with a probability of 0.5 it determines whether or not to believe the reward. |
||
|
You can build an inappropriate machine. For example, "Ivan the Fool" is a machine gun with two actions (crying and laughing) and a depth of 1. |
||
fig.3.5
|
||
Which depth is better?Figure 3.6 shows a graph of the feasibility of the depth, taking into account the frequency of changes in the environment. It is best to adjust the value of q depending on the environment. |
||
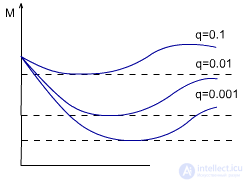
ris.3.6
|
||
Collective of automata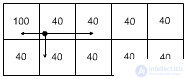
ris.3.7
|
||
|
Given the resource field. In each cell there is a machine with linear tactics (4.4). For definiteness, let's leave 10 automata. The machine can implement the following actions: stay in place, go right, go left, go up (down). |
||
|
From the point of view of public benefit, the first situation is better, since on average, "per capita" a higher result. But from the point of view of individual benefit, the second situation is better. The first was named the game Mora, the second - the game Nash. A sustainable team is one where everyone is guided by their own benefit. |
||
|
But is it possible to play sustainable game Mora? Those. get the maximum public benefit, while maintaining a steady state. This requires playing a game with a common cash register: everyone plays the game of Mora, but then everything is divided equally. |
||
|
If the machines have a large q, then it is more profitable for them to play the game of Mora, since they are more inertial; and vice versa - if q is low, then in the Nash game, because they are more active. |
||
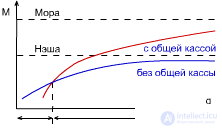
ris.3.8
|
||
|
But do all environments have similar properties? There are environments that do not obey the above conclusions. |
||
|
||
|
Figure 3.9 - picking mushrooms. In Figure 3.10 - hunting for elk. |
Comments
To leave a comment
Artificial Intelligence
Terms: Artificial Intelligence