Lecture
Example: There are 2 production sites that employ 100 workers. The task is to place them in sections in the best way, i.e. find the ratio x: y. The economic situation in 1 segment: 400x - 0.02x 2 = S x ; in the second - 280y - 0.4y 2 = S y , where x is the number of workers in the first section, y is in the second, S x, y is the income from the sections. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Explanation: The negative term symbolizes the restriction on the scope of work, many individuals interfere with each other. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The coefficient of x and y indicates the possibility of earning a single individual and depends on the properties of the environment (area). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Consider the options: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Option A {80.20} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Because The average wage at the sites is the same; workers will not move from one site to another. We will have a steady state. Nash game. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
B - {51.49} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This situation is more beneficial in the public sense (more money is received). But due to the fact that the average salary is not the same (when moving from the second section to the first, the individual will receive an additional 88 rubles for the same job), the situation will not be sustainable. Game Mora. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Zetlin: "Inequality in payment is equivalent to the benefit of public interest." | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
But if you need to simultaneously combine the maximum of the social income of the game of Mora and the stability of the game of Nesh, then you must follow the rules of the game with a common cash register: everyone plays the game of Mora, but then everything is assembled into a common cash register and is divided into all. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Variable Structure MachineIn an automatic machine with a linear structure, one of the main parameters is the lobe depth - q. In a non-stationary environment, q should be small; in stationary - on the contrary. It is required to build an automaton that would determine for itself the quantity q. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Self studyAn example showing that a machine, initially untrained, starts playing better than a teacher. Tic-tac-toe game. For convenience, we assume that the teacher plays with zeroes and always makes the first move. Accordingly, the machine plays with crosses. Suppose that for the first time the machine has lost. Therefore, the probability of all transitions leading to loss decreases. On the 3x3 field, after 20-30 games, the machine will at least reduce all games to a draw. Read more | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nature of learningIs it possible to give a character to learning, i.e. give the machine some individual traits, make a variety. For example, an automaton wants to marry and the main criteria for its decision are such parameters as the presence of an apartment and the ability to cook. x = f (y 1 ; y 2 ) , where x is the output solution, y 1 , y 2 are input signals (let y 1 be the presence of an apartment, y 2 the ability to cook). All variables take one of the three values {0, 0.5, 1}, i.e. “no”, “like yes, and maybe not”, “yes”. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The most sustainable society: 40% impassive; 40% of moderate pessimists; 20% moderate optimists. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 fig.4.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Homogeneous structuresThe system is described by three components Q, R, I (goal, resources, information). These components are inherent in both the system and its elements. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Examples of various systems: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Systems are divided into centralized and decentralized (Figure 4.7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
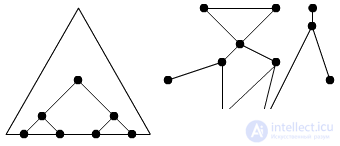 fig.4.7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Decentralized systems are usually naturally formed systems, for example, the human body, the international telephone network, the Internet, and the worldwide organization of philatelists. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Characteristics of a centralized system | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Characteristics of a decentralized system | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Comments
To leave a comment
Artificial Intelligence
Terms: Artificial Intelligence