Lecture
If the flow of events is non-stationary, then its main characteristic is instantaneous density. 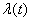 . The instantaneous flux density is the limit of the ratio of the average number of events per elementary time interval.
. The instantaneous flux density is the limit of the ratio of the average number of events per elementary time interval. 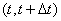 , to the length of this section, when the latter tends to zero:
, to the length of this section, when the latter tends to zero:
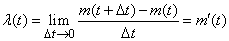 , (19.4.1)
, (19.4.1)
Where 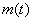 - mathematical expectation of the number of events at the site
- mathematical expectation of the number of events at the site 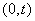 .
.
Consider the flow of homogeneous events, ordinary and without aftereffect, but not stationary, with variable density 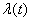 . Such a stream is called a non-stationary Poisson stream. This is the first step of generalization compared to the simplest flow. It is easy to show a method similar to that used in
. Such a stream is called a non-stationary Poisson stream. This is the first step of generalization compared to the simplest flow. It is easy to show a method similar to that used in  5.9, that for such a stream the number of events falling on the length segment
5.9, that for such a stream the number of events falling on the length segment 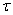 starting at point
starting at point 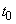 obeys the Poisson law
obeys the Poisson law
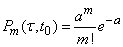
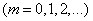 , (19.4.2)
, (19.4.2)
Where 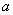 - mathematical expectation of the number of events in the area from
- mathematical expectation of the number of events in the area from 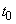 before
before 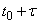 equal to
equal to
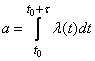 . (19.4.3)
. (19.4.3)
Here is the value 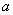 depends not only on length
depends not only on length 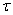 plot, but also from its position on the axis
plot, but also from its position on the axis 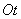 .
.
We find for a nonstationary flow the distribution law of the time interval 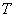 between neighboring events. Due to the nonstationarity of the flow, this law will depend on where on the axis
between neighboring events. Due to the nonstationarity of the flow, this law will depend on where on the axis 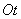 The first event is located. In addition, it will depend on the type of function
The first event is located. In addition, it will depend on the type of function 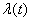 . Suppose that the first of two adjacent events appeared at the moment
. Suppose that the first of two adjacent events appeared at the moment 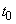 and find under this condition the law of time distribution
and find under this condition the law of time distribution 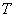 between this event and the following:
between this event and the following:
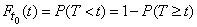 .
.
We find 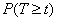 - the probability that in the area from
- the probability that in the area from 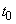 before
before 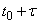 no events will appear:
no events will appear:
 ,
,
from where
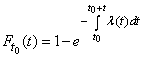 . (19.4.4)
. (19.4.4)
Differentiating, we find the distribution density
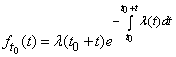
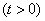 . (19.4.5)
. (19.4.5)
This distribution law is no longer indicative. Its appearance depends on the parameter. 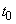 and kind of function
and kind of function 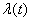 . For example, with a linear change
. For example, with a linear change 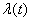
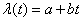
density (19.4.5) is
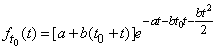 . (19.4.6)
. (19.4.6)
The schedule of this law is 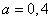 ;
; 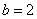 and
and 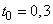 presented in fig. 19.4.1.
presented in fig. 19.4.1.
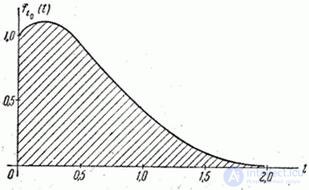
Fig. 19.4.1.
Despite the fact that the structure of a nonstationary Poisson flow is somewhat more complicated than the simplest one, it is very convenient in practical applications: the main property of the simplest flow — the absence of aftereffect — is preserved in it. Namely, if we fix on the axis  arbitrary point
arbitrary point 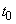 then the distribution law
then the distribution law 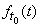 of time
of time 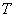 , separating this point from the nearest future event, does not depend on what happened at the time interval preceding
, separating this point from the nearest future event, does not depend on what happened at the time interval preceding 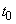 and at the very point
and at the very point 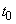 (i.e., whether other events have appeared earlier and when).
(i.e., whether other events have appeared earlier and when).
Comments
To leave a comment
Queuing theory
Terms: Queuing theory