19.5. Stream with limited aftereffect (stream Palma)

In the previous we got acquainted with the natural generalization of the simplest flow — the unsteady Poisson flow. A generalization of the simplest flow in the other direction is a flow with limited aftereffect.

Consider the ordinary stream of homogeneous events (Fig. 19.5.1).

Fig. 19.5.1.

This stream is called a stream with limited aftereffect (or a Palma stream) if the intervals between successive events 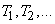are independent random variables.

Obviously, the simplest flow is a special case of the flow of Palma: there are distances in it. 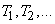are independent random variables distributed according to exponential law. As for the unsteady Poisson flow, it is not a Palma flow. Indeed, consider the two adjacent intervals 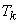and 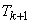in non-stationary Poisson flow. As we saw in the previous , the law of distribution of the gap between events in a non-stationary stream depends on where this gap begins, and the beginning of the gap 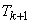coincides with the end of the gap 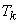; This means that the lengths of these intervals are dependent.

Consider the examples of Palma flows.

1. Some part of a technical device (for example, a radio tube) works continuously until its failure (failure), after which it is instantly replaced by a new one. The term of no-failure operation is accidental; some instances fail independently of each other. Under these conditions, the flow of failures (or the flow of "recovery") is the flow of Palm. If, moreover, the period of work of the part is distributed according to the exponential law, then the Palm flow turns into the simplest one.

2. A group of aircraft goes into battle order "column" (Fig. 19.5.2) with the same speed for all aircraft 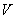. Each aircraft, except the lead, is obliged to maintain operation, i.e. to keep at a given distance 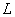from going ahead. This distance, due to the errors of the radio range finder, is maintained with errors. The moments of the intersection of a given line of aircraft form a stream of Palma, since random variables 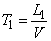; ; 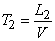... are independent. Note that the same flow will not be the flow of Palma, if each of the aircraft tends to maintain a given distance not from the neighbor, but from the leader.

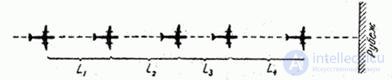
Fig. 19.5.2.

Palma flows are often obtained as output flows of queuing systems. If any system receives a stream of requests, then it is divided into two by this system: the stream of serviced and the stream of unserved requests.

The flow of unserved applications is often sent to some other queuing system, so it is of interest to study its properties.

The main one in the theory of output flows is the Palma theorem, which we state without proof.

Let the flow of requests like Palma arrive at the queuing system, and an application that has made all channels busy gets rejected (not served). If, at the same time, the service time has an exponential distribution law, then the flow of unserved applications is also a Palm type flow.

In particular, if the input flow of applications is the simplest, then the stream of unserved applications, without being the simplest, will still have a limited follow-up.

An interesting example of streams with limited aftereffect is the so-called Erlang streams. They are formed by "screening" the simplest flow.

Consider the simplest flow (Fig. 19.5.3) and discard every second point from it (in the figure, the ejected points are marked with crosses).

Fig. 19.5.3.

The remaining points form a stream; this flow is called the first order Erlang flow 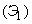. Obviously, this flow is the Palm flow: since the intervals between events in the simplest flow are independent, the values 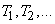, obtained by summing up such intervals in two.

The second-order Erlang flow will be obtained if every third point is kept in the simplest flow, and two intermediate points are discarded (Fig. 19.5.4).

Fig. 19.5.4.

In general, the k-th order Erlang flow 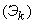called a stream derived from the simplest if you save each 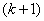point and throw the rest. Obviously, the simplest flow can be considered as a zero order Erlang flow. .

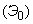Find the distribution law of the time interval 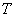between neighboring events in the Erlang stream 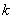th order 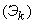. Consider on the axis (fig. 19.5.5) the simplest flow with intervals

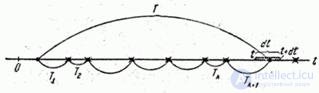
Fig. 19.5.5.

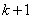Magnitude represents the sum independent random variables

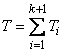, (19.5.1)

Where 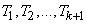- independent random variables subject to the same indicative law

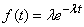
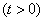. (19.5.2)

It would be possible to find the distribution law 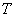as a composition 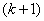laws (19.5.2). However, it is easier to derive it by elementary reasoning.

Denote 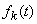distribution density 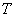for flow 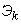; 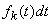there is a probability that the magnitude 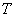will take the value between 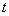and 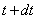(fig. 19.5.5). This means that the last point of the gap 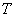should get to the elementary site 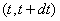and previous 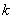points of the simplest flow - on the plot 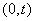. The probability of the first event is equal to 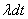the probability of the second, based on the formula (19.3.2), will be

.

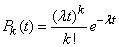Multiplying these probabilities, we get

,

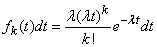from where

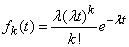
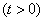. (19.5.3)

The distribution law with density (19.5.3) is called the Erlang law 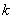th order. Obviously when 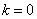he turns into indicative

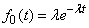
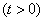. (19.5.4)

Find the characteristics of the Erlang law 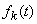: expected value 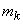and variance 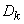. By the theorem of addition of mathematical expectations

,

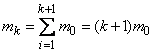Where 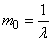- expectation of the gap between events in the simplest flow.

From here

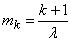. (19.5.5)

Similarly, by the addition theorem

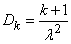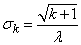, . (19.5.6)

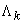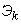Density flow will be the opposite of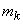

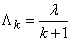. (19.5.7)

Thus, with an increase in the order of the Erlang flow, both the expectation and the variance of the time interval between events increase, and the density of the flow decreases.

Find out how the Erlang flow will change when 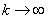if its density will be kept constant? We normalize 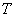so that its expectation (and, therefore, flux density) remains unchanged. To do this, change the scale along the time axis and instead of 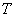consider the value

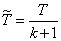. (19.5.8)

Let's call such a stream the normal Erlang flow 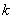th order. Gap distribution law 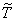between the events of this thread will be

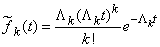
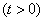, (19.5.9)

Where 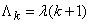, or

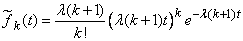
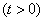. (19.5.10)

Expectation value 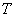distributed according to the law (19.5.10) does not depend on 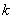and equals

,

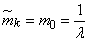Where 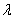- the flux density coinciding with any 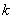with the density of the original simplest flow. Variance of magnitude 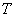equals

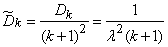(19.5.11)

and decreases indefinitely with increasing .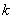

Thus, we conclude: with an unlimited increase 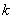the normal Erlang flow approaches a regular flow with constant intervals equal to .

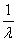This property of the Erlang flows is convenient in practical applications: it gives the possibility, by asking various 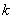, get any degree of aftereffect: from total absence 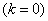up to a hard functional connection between the events 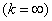. Thus, the order of the flow of the Erlang can serve as a "measure of the aftereffect" existing in the flow. In order to simplify, it is often convenient to replace the real flow of applications, which has an after-effect, with the normalized Erlang flow with approximately the same characteristics of the gap between applications: expected value and variance.

Example. As a result of statistical processing of the intervals between applications in the stream, estimates are obtained for the expectation and variance of :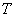

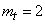(min) 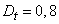(min2)

Replace this stream with a normal Erlang stream with the same characteristics.

Decision. We have

.

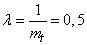From the formula (19.5.11) we get

, .

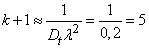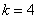The flow can be approximately replaced by a fourth-order normalized Erlang flow.