Lecture
Will consider 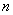 -channel queuing system with failures, the input of which receives the simplest flow of requests with a density
-channel queuing system with failures, the input of which receives the simplest flow of requests with a density 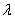 ; service time - indicative, with parameter
; service time - indicative, with parameter 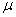 . The question arises: will the random process occurring in the system be stationary? Obviously, in the beginning, immediately after the system is put into operation, the process proceeding in it will not yet be stationary: a so-called “transient”, non-stationary process will arise in a queuing system (as in any dynamic system). However, after some time, this transition process will die out, and the system will switch to a stationary, so-called “steady” mode, the probabilistic characteristics of which will no longer depend on time.
. The question arises: will the random process occurring in the system be stationary? Obviously, in the beginning, immediately after the system is put into operation, the process proceeding in it will not yet be stationary: a so-called “transient”, non-stationary process will arise in a queuing system (as in any dynamic system). However, after some time, this transition process will die out, and the system will switch to a stationary, so-called “steady” mode, the probabilistic characteristics of which will no longer depend on time.
In many practical tasks, we are interested in the characteristics of the limit established service regime.
It can be proved that for any system with failures such a limiting mode exists, i.e. 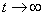 all probabilities
all probabilities 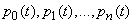 aim for constant limits
aim for constant limits 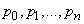 , and all their derivatives - to zero.
, and all their derivatives - to zero.
To find the marginal probabilities 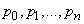 (the probabilities of the states of the system in the steady state), we replace in the equations (19.8.8) all the probabilities
(the probabilities of the states of the system in the steady state), we replace in the equations (19.8.8) all the probabilities 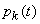
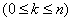 their limits
their limits 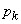 , and all derivatives are set equal to zero. We get the system is not differential, and algebraic equations
, and all derivatives are set equal to zero. We get the system is not differential, and algebraic equations
 (19.9.1)
(19.9.1)
To these equations you must add the condition
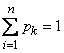 . (19.9.2)
. (19.9.2)
Solve the system (19.9.1) relatively unknown 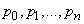 . From the first equation we have
. From the first equation we have
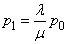 . (19.9.3)
. (19.9.3)
From the second, taking into account (19.9.3),
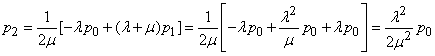 ; (19.9.4)
; (19.9.4)
similarly from the third one, taking into account (19.9.3) and (19.9.4),
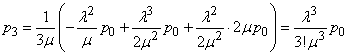 ,
,
and in general, for any 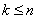
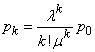 . (19.9.5)
. (19.9.5)
We introduce the notation
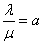 (19.9.6)
(19.9.6)
and let's call the value 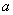 reduced density of applications. This is nothing more than the average number of applications per average service time for one application. Really,
reduced density of applications. This is nothing more than the average number of applications per average service time for one application. Really,
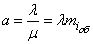 ,
,
Where 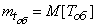 - average time of servicing a single application. In the new notation, the formula (19.9.5) takes the form
- average time of servicing a single application. In the new notation, the formula (19.9.5) takes the form
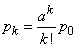 . (19.9.7)
. (19.9.7)
Formula (19.9.7) expresses all probabilities 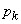 through
through 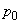 . To express them directly through
. To express them directly through 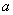 and
and 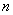 , we use the condition (19.9.2). Substituting into it (19.9.7), we get
, we use the condition (19.9.2). Substituting into it (19.9.7), we get
 ,
,
from where
 . (19.9.8)
. (19.9.8)
Substituting (19.9.8) into (19.9.7), we finally get

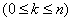 . (19.9.9)
. (19.9.9)
Formulas (19.9.9) are called Erlang formulas. They give the limiting law of distribution of the number of occupied channels depending on the characteristics of the flow of requests and the performance of the service system. Assuming in the formula (19.9.9) 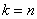 , we get the probability of failure (the likelihood that the incoming application will find all channels occupied):
, we get the probability of failure (the likelihood that the incoming application will find all channels occupied):
 . (19.9.10)
. (19.9.10)
In particular, for a single-channel system ( 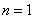 )
)
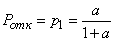 , (19.9.11)
, (19.9.11)
and the relative bandwidth
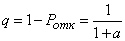 . (19.9.12)
. (19.9.12)
Erlang's formulas (19.9.9) and their corollaries (19.9.10) - (19.9.12) are derived by us for the case of an exponential distribution of the service time. However, studies of recent years have shown that these formulas remain valid even under any law of the distribution of service time, so long as the input flow is the simplest.
Example 1. An automatic telephone exchange has 4 communication lines. The station receives the simplest flow of applications with a density 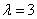 (call per minute). The call received at the moment when all the lines are busy receives a rejection. Average talk time is 2 minutes. Find: a) probability of failure; b) the average share of time during which the telephone exchange is not loaded at all.
(call per minute). The call received at the moment when all the lines are busy receives a rejection. Average talk time is 2 minutes. Find: a) probability of failure; b) the average share of time during which the telephone exchange is not loaded at all.
Decision. We have 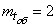 (min);
(min);
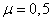 (g / min)
(g / min) 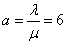 .
.
a) According to the formula (19.9.10) we get
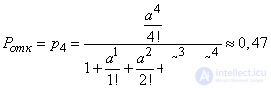 .
.
b) According to the formula (19.9.8)
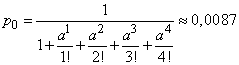 .
.
Despite the fact that the Erlang formulas are exactly valid only for the simplest flow of applications, they can be used with a certain approximation in the case when the flow of applications differs from the simplest (for example, it is a stationary flow with limited aftereffect). Calculations show that the replacement of an arbitrary stationary flow with a not very large aftereffect by the simplest flow of the same density  As a rule, it has little effect on the characteristics of the system bandwidth.
As a rule, it has little effect on the characteristics of the system bandwidth.
Finally, it can be noted that the Erlang formulas can be approximately used also in the case when the queuing system allows waiting for an application in a queue, but when the waiting time is small compared to the average service time of a single application.
Example 2. A fighter guidance station has 3 channels. Each channel can simultaneously direct one fighter at a single target. The average time of targeting a fighter at the target 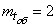 min The flow of targets is the simplest, with a density
min The flow of targets is the simplest, with a density 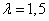 (planes per minute). The station can be considered a “system with refusals”, since the goal for which the guidance did not start at the moment when it entered the fighter action zone, in general, remains unattacked. Find the average share of targets passing through the area not shot at.
(planes per minute). The station can be considered a “system with refusals”, since the goal for which the guidance did not start at the moment when it entered the fighter action zone, in general, remains unattacked. Find the average share of targets passing through the area not shot at.
Decision. We have 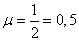 ;
; 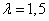 ;
; 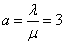 .
.
According to the formula (19.9.10)
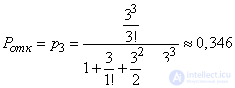 .
.
Probability of failure  ; it also expresses the average share of undefiled targets.
; it also expresses the average share of undefiled targets.
Note that in this example, the target flux density is chosen such that when they are regularly followed one after another at certain intervals and at exactly fixed guidance time 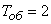 Min. The nominal capacity of the system is sufficient to fire at all targets without exception. The reduction in throughput is due to the presence of random condensations and rarefactions in the flow of targets that cannot be foreseen in advance.
Min. The nominal capacity of the system is sufficient to fire at all targets without exception. The reduction in throughput is due to the presence of random condensations and rarefactions in the flow of targets that cannot be foreseen in advance.
Comments
To leave a comment
Queuing theory
Terms: Queuing theory