Lecture
In addition to the characteristics of the input flow of requests, the mode of operation of the system also depends on the performance characteristics of the system itself: the number of channels 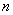 and speed of each channel. One of the most important values associated with the system is the time of servicing a single application.
and speed of each channel. One of the most important values associated with the system is the time of servicing a single application. 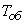 . This value can be either non-random or random. Obviously, the more common is the random maintenance time.
. This value can be either non-random or random. Obviously, the more common is the random maintenance time.
Consider a random variable 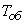 and denote
and denote 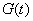 its distribution function is:
its distribution function is:
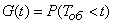 , (19.6.1)
, (19.6.1)
a 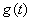 - distribution density:
- distribution density:
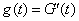 . (19.6.2)
. (19.6.2)
For practice, of particular interest is the case when the magnitude 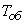 has exponential distribution
has exponential distribution
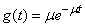
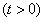 , (19.6.3)
, (19.6.3)
where is the parameter 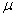 - the inverse of the average service time of a single application:
- the inverse of the average service time of a single application:
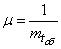 ,
, 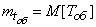 . (19.6.4)
. (19.6.4)
The special role that the exponential distribution law  associated with the property of this law, which was proved in
associated with the property of this law, which was proved in  19.4. As applied to this case, it is formulated as follows: if at some point
19.4. As applied to this case, it is formulated as follows: if at some point  the application is serviced, then the law of distribution of the remaining service time does not depend on how long the service has been going on.
the application is serviced, then the law of distribution of the remaining service time does not depend on how long the service has been going on.
At first glance, the assumption that service time is distributed according to the exponential law seems rather artificial. In a number of practical problems, it seems more natural to assume that it is either not at all random or distributed according to a normal law. However, there are conditions in which the maintenance time is really distributed according to a law close to the exponential.
These are, first of all, all tasks in which maintenance is reduced to a number of “attempts”, each of which leads to the necessary result with some probability 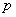 .
.
Let, for example, “service” consist in the shelling of a target and end at the moment of its defeat. The shelling is carried out by independent shots with some average rate of fire. 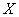 shots per unit of time. Each shot hits a target with probability
shots per unit of time. Each shot hits a target with probability 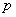 . In order not to bind ourselves with the need to accurately account for the moment of each shot, suppose that they occur at random times and form the simplest flow.
. In order not to bind ourselves with the need to accurately account for the moment of each shot, suppose that they occur at random times and form the simplest flow. 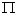 with density
with density 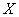 (fig. 19.6.1).
(fig. 19.6.1).

Fig. 19.6.1.
Let us mentally select from this stream another - the stream of “successful” or “striking” shots (they are marked with circles in Fig. 19.6.1). A shot will be called “successful” if it results in defeat of the target (unless the target was previously hit). It is easy to make sure that successful shots also form the simplest flow. 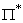 with density
with density 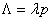 (source stream
(source stream 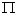 - the simplest, and each shot can be striking, independently of the others, with probability
- the simplest, and each shot can be striking, independently of the others, with probability 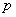 ). The likelihood that the target will be hit until
). The likelihood that the target will be hit until 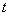 will be equal to
will be equal to
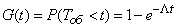 ,
,
where the density of the distribution of time "service"
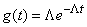 ,
,
And this is indicative of the law with the parameter 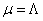 .
.
The exponential law of the distribution of firing time before hitting a target can be approximately used even when the shots do not form the simplest flow, but are separated, for example, by strictly defined periods of time.  , if only the probability of hitting one shot
, if only the probability of hitting one shot 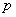 not very great. For illustration, on the same graph (Fig. 19.6.2) we present the moment distribution function of the striking shot (stepped line) for the case
not very great. For illustration, on the same graph (Fig. 19.6.2) we present the moment distribution function of the striking shot (stepped line) for the case 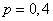 ,
, 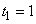 and the distribution function of exponential law with parameter
and the distribution function of exponential law with parameter 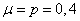 (smooth curve).
(smooth curve).
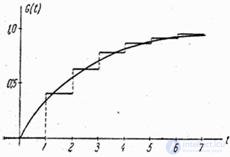
Fig. 19.6.2.
As seen in fig. 19.6.2, the continuous exponential distribution fits well with the growth pattern of the distribution function for the discrete case. Naturally, if the moments of the shots are not strictly defined, compliance with exemplary law will be even better.
The shooting case is not the only one when maintenance is carried out alongside a number of “attempts”. This type of service often includes troubleshooting maintenance of technical devices when searching for a faulty part or assembly is carried out by a series of tests or checks. To the same type can be attributed to the problem, where the "maintenance" is the detection of any object by radar, if the object with some probability can be detected during each cycle of the review.
The exemplary law describes well those cases where the density of distribution of the service time for one reason or another decreases with increasing argument 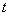 . This happens when the majority of requests are serviced very quickly, and significant service delays are rarely observed. Consider, for example, the post office window, where stamps and envelopes are sold, as well as mailings and money transfers. The bulk of visitors buy stamps or envelopes and serviced very quickly. Less common are applications for sending registered letters, they are served a little longer. Transfers are sent even less often and serviced even longer. Finally, in the rarest cases, representatives of organizations send a large number of letters at once. The histogram of the distribution of service time has the form shown in Fig. 19.6.3.
. This happens when the majority of requests are serviced very quickly, and significant service delays are rarely observed. Consider, for example, the post office window, where stamps and envelopes are sold, as well as mailings and money transfers. The bulk of visitors buy stamps or envelopes and serviced very quickly. Less common are applications for sending registered letters, they are served a little longer. Transfers are sent even less often and serviced even longer. Finally, in the rarest cases, representatives of organizations send a large number of letters at once. The histogram of the distribution of service time has the form shown in Fig. 19.6.3.
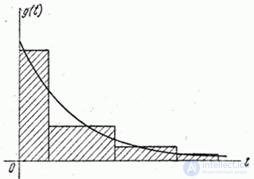
Fig. 19.6.3.
Since the distribution density decreases with increasing 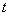 It is possible to evenly distribute the distribution with a special law, by selecting its parameter accordingly.
It is possible to evenly distribute the distribution with a special law, by selecting its parameter accordingly. 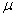 .
.
Of course, the indicative law is not a universal law of the distribution of service time. Often the maintenance time is better described, for example, by Erlang law. However, fortunately, the capacity and other characteristics of a queuing system depend relatively little on the type of distribution law of the service time, and depend mainly on its average value. 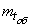 . Therefore, in the theory of queuing, it is often assumed that service time is distributed according to the exponential law. This hypothesis makes it possible to greatly simplify the mathematical apparatus used to solve problems of mass service, and, in some cases, to obtain simple analytical formulas for the characteristics of the system capacity.
. Therefore, in the theory of queuing, it is often assumed that service time is distributed according to the exponential law. This hypothesis makes it possible to greatly simplify the mathematical apparatus used to solve problems of mass service, and, in some cases, to obtain simple analytical formulas for the characteristics of the system capacity.
Comments
To leave a comment
Queuing theory
Terms: Queuing theory