You get a bonus - 1 coin for daily activity. Now you have 1 coin

19.2. Random process with a countable set of states

Lecture



A random process occurring in a queuing system consists in the fact that the system moves from one state to another at random times: the number of busy channels, the number of requests in the queue, etc., changes. This process differs significantly from random processes which we covered in chapters 15-17. The fact is that the queuing system is a discrete-type physical system with a finite (or countable) set of states, and the transition of the system from one state to another occurs abruptly, at the moment when an event occurs (the arrival of a new application, the release of the channel , withdrawal of the application from the queue, etc.).

Consider the physical system 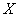19.2. Random process with a countable set of states with a countable set of states

19.2. Random process with a countable set of states .

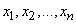At any given time 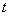19.2. Random process with a countable set of states system 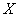19.2. Random process with a countable set of states may be in one of these states. Denote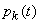 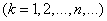19.2. Random process with a countable set of states 19.2. Random process with a countable set of states probability that at the moment 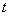19.2. Random process with a countable set of states the system will be able to 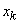19.2. Random process with a countable set of states . 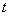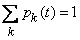Obviously for any 19.2. Random process with a countable set of states

19.2. Random process with a countable set of states . (19.2.1)

Set of probabilities 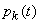19.2. Random process with a countable set of states for each point in time 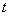19.2. Random process with a countable set of states characterizes a given cross section of a random process occurring in the system. This set is not an exhaustive characteristic of the process (it, for example, does not at all reflect the relationship between sections), but it still describes the process quite well and is sufficient for a number of practical applications.

Random processes with a countable set of states are of two types: with discrete or continuous time. The former are distinguished by the fact that transitions from state to state can occur only at strictly defined moments of time separated by finite intervals. 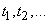19.2. Random process with a countable set of states . Continuous time random processes are distinguished by the fact that the transition of a system from state to state is possible at any time. 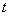19.2. Random process with a countable set of states .

As an example of a discrete system 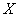19.2. Random process with a countable set of states in which a random process with continuous time flows, consider a group of 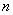19.2. Random process with a countable set of states airplanes making raids on enemy territory, defended by fighter aircraft. Neither the moment of discovery of the group, nor the moments of lifting fighters on it are known in advance. The various states of the system correspond to the different number of aircraft involved in the group:

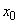19.2. Random process with a countable set of states - not a single aircraft hit,

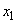19.2. Random process with a countable set of states - exactly one plane was hit,

………….

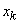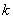19.2. Random process with a countable set of states - exactly struck 19.2. Random process with a countable set of states airplanes

………….

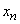19.2. Random process with a countable set of states - all amazed 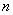19.2. Random process with a countable set of states aircraft.

A diagram of possible system states and possible transitions from state to state is shown in Fig. 19.2.1.

19.2. Random process with a countable set of states

Fig. 19.2.1.

The arrows indicate the possible transitions of the system from state to state. Rounded arrow pointing out of state 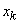19.2. Random process with a countable set of states it also means that the system can not only go into a neighboring state, but also remain the same. Irreversible transitions are typical for this system (the affected aircraft are not restored); in this regard from the state 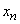19.2. Random process with a countable set of states no transitions to other states are already possible.

Note that the diagram of possible transitions (Fig. 19.2.1) shows only transitions from a state to a neighboring state and does not show “jumps” through the state: these jumps are rejected as practically impossible. Indeed, in order for the system to "jump" through the state, it is necessary that two or more aircraft be hit strictly simultaneously, and the probability of such an event is zero.

Random processes occurring in queuing systems, as a rule, are processes with continuous time. This is due to the randomness of the flow of applications. In contrast to the system with irreversible transitions, considered in the previous example, reversible transitions are characteristic of a queuing system: a busy channel can become free, the queue can “dissolve”.

As an example, consider a single-channel queuing system (for example, one telephone line) in which the application that made the channel busy does not get in the queue, but leaves the system (receives a “rejection”). This is a discrete system with continuous time and two possible states:

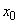19.2. Random process with a countable set of states - the channel is free,

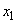19.2. Random process with a countable set of states - the channel is busy.

Transitions from state to state are reversible. The scheme of possible transitions is shown in Fig. 19.2.2.

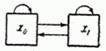
19.2. Random process with a countable set of states

Fig. 19.2.2.

For 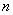19.2. Random process with a countable set of states -channel system of the same type the scheme of possible transitions is shown in Fig. 19.2.3.

19.2. Random process with a countable set of states

Fig. 19.2.3.

condition 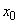19.2. Random process with a countable set of states - all channels are free; 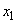19.2. Random process with a countable set of states - exactly one channel is busy, 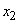19.2. Random process with a countable set of states - exactly two channels are occupied, etc.

Consider another example of a discrete system with continuous time: a single-channel queuing system, which can be in four states:

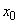19.2. Random process with a countable set of states - the channel is healthy and free,

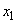19.2. Random process with a countable set of states - the channel is healthy and busy,

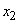19.2. Random process with a countable set of states - the channel is faulty and is waiting for repair,

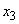19.2. Random process with a countable set of states - The channel is faulty and repaired.

The scheme of possible transitions for this case is shown in Fig. 19.2.4.

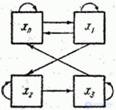
19.2. Random process with a countable set of states

Fig. 19.2.4.

Transition system from 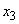19.2. Random process with a countable set of states directly in 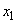19.2. Random process with a countable set of states bypassing 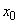19.2. Random process with a countable set of states can be considered almost impossible, since for this it is necessary that the end of the repair and the arrival of the next application take place strictly at the same time.

In order to describe a random process occurring in a discrete system with continuous time, first of all, it is necessary to analyze the reasons causing the system to transition from state to state. For a queuing system, the main factor determining the processes occurring in it is the flow of requests. Therefore, the mathematical description of any queuing system begins with a description of the flow of requests.

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Queuing theory

Terms: Queuing theory