Lecture
Queuing systems are divided into two main types: a) systems with failures, b) systems with waiting.
In systems with refusals, an application that arrived at the moment when all service channels are busy immediately receives a refusal, leaves the system and does not participate in the further maintenance process.
In systems with waiting, an application that has made all channels busy does not leave the system, but becomes in a queue and waits until a channel becomes free. Present 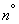 we will consider the system with failures as the simplest.
we will consider the system with failures as the simplest.
Let there be 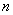 -channel queuing system with failures. Consider it as a physical system.
-channel queuing system with failures. Consider it as a physical system. 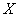 with a finite set of states:
with a finite set of states:
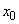 - all channels are free,
- all channels are free,
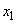 - exactly one channel is busy,
- exactly one channel is busy,
……………
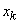 - busy exactly
- busy exactly 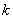 channels,
channels,
……………
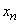 - all busy
- all busy 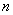 channels.
channels.
The scheme of possible transitions is given in fig. 19.8.1.

Fig. 19.8.1.
We set the task: to determine the probabilities of the system states 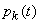
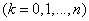 for any point in time
for any point in time 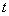 . The task will be solved under the following assumptions:
. The task will be solved under the following assumptions:
1) the flow of applications - the simplest, with a density
2) service time 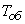 - indicative, with parameter
- indicative, with parameter 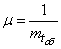
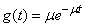 .
. 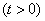 . (19.8.1)
. (19.8.1)
Note that the parameter 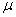 in the formula (19.8.1) is completely analogous to the parameter
in the formula (19.8.1) is completely analogous to the parameter 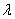 exponential law of distribution of the gap
exponential law of distribution of the gap 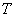 between neighboring events of the simplest flow:
between neighboring events of the simplest flow:
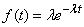
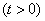 . (19.8.2)
. (19.8.2)
Parameter 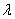 makes sense of "flow density applications." Similarly, the value
makes sense of "flow density applications." Similarly, the value 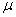 can be interpreted as the “release flux density” of a busy channel. Indeed, let us imagine a channel that is continuously occupied (uninterruptedly supplied with applications); then, obviously, in this channel there will be a simple stream of releases with a density
can be interpreted as the “release flux density” of a busy channel. Indeed, let us imagine a channel that is continuously occupied (uninterruptedly supplied with applications); then, obviously, in this channel there will be a simple stream of releases with a density 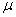 .
.
Since both flows — applications and exemptions — are the simplest, the process going on in the system will be Markov.
Consider the possible system states and their probabilities.
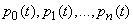 . (19.8.3)
. (19.8.3)
Obviously for any point in time
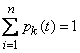 . (19.8.4)
. (19.8.4)
Create differential equations for all probabilities (19.8.3), starting with 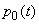 . Fix a point in time
. Fix a point in time 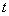 and find the probability
and find the probability 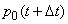 that at the moment
that at the moment 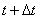 the system will be able to
the system will be able to 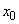 (all channels are free). This can happen in two ways (Fig. 19.8.2):
(all channels are free). This can happen in two ways (Fig. 19.8.2):
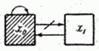
Fig. 19.8.2.
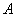 - in the moment
- in the moment 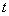 the system was able to
the system was able to 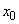 and in time
and in time 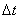 did not pass from it to
did not pass from it to 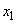 (not a single application has arrived)
(not a single application has arrived)
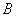 - in the moment
- in the moment 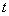 the system was able to
the system was able to 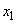 and in time
and in time 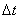 the channel was released, and the system went into a state
the channel was released, and the system went into a state 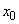 .
.
The ability to "jump" the system through the state (for example, from 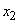 at
at 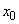 through
through 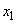 ) for a small period of time can be neglected, as the value of a higher order of smallness compared with
) for a small period of time can be neglected, as the value of a higher order of smallness compared with 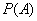 and
and 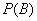 .
.
By the addition theorem, we have
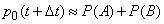 . (19.8.5)
. (19.8.5)
Find the probability of the event 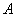 by the multiplication theorem. Probability that at the moment
by the multiplication theorem. Probability that at the moment 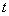 the system was able to
the system was able to 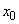 equal to
equal to 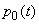 . Probability that for time
. Probability that for time 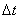 will not come any application equal
will not come any application equal 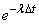 . Up to values of the highest order of smallness
. Up to values of the highest order of smallness
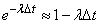 . (19.8.6)
. (19.8.6)
Consequently,
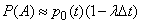 .
.
We find 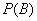 . Probability that at the moment
. Probability that at the moment 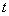 the system was able to
the system was able to 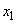 equal to
equal to 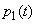 . Probability that for time
. Probability that for time 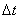 the channel is free, equal to
the channel is free, equal to 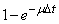 up to low order values
up to low order values
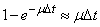 .
.
Consequently,
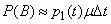 .
.
From here
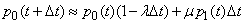 .
.
Shifting 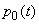 to the left by dividing by
to the left by dividing by 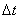 and going to the limit at
and going to the limit at 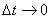 , we obtain the differential equation for
, we obtain the differential equation for 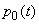 :
:
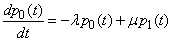 . (19.8.7)
. (19.8.7)
Similar differential equations can be compiled for other probabilities of states.
Take any 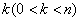 and find the probability
and find the probability 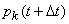 that at the moment
that at the moment 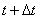 the system will be able to
the system will be able to 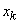 (fig. 19.8.3).
(fig. 19.8.3).
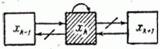
Fig. 19.8.3.
This probability is calculated as the probability of the sum of not two, but three events (according to the number of arrows directed to 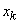 ):
):
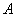 - in the moment
- in the moment 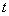 the system was able to
the system was able to 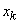 (busy)
(busy) 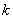 channels), and in time
channels), and in time 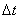 did not pass from him to any
did not pass from him to any 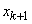 nor in
nor in 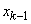 (not a single application has been received, not a single channel has been released);
(not a single application has been received, not a single channel has been released);
 - in the moment
- in the moment 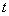 the system was able to
the system was able to 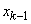 (busy)
(busy) 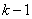 channels), and in time
channels), and in time 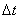 moved to
moved to 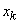 (one application has arrived);
(one application has arrived);
 - in the moment
- in the moment 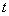 the system was able to
the system was able to 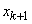 (busy)
(busy) 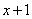 channels), and in time
channels), and in time 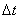 one of the channels is free.
one of the channels is free.
We find 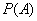 . We first calculate the probability that in time
. We first calculate the probability that in time 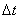 No application will come and none of the channels will be released:
No application will come and none of the channels will be released:
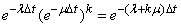 .
.
Neglecting small values of higher orders, we have
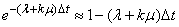 ,
,
from where
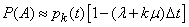 .
.
Similarly
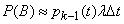 ,
,
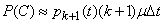
and
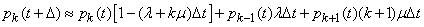 .
.
From here we get the differential equation for 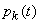
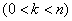 :
:
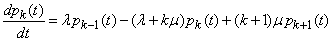 .
.
Let's make the equation for the last probability 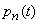 (fig. 19.8.4).
(fig. 19.8.4).
Fig. 19.8.4.
We have
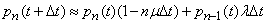 ,
,
Where 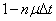 - the probability that in time
- the probability that in time 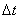 no channel is free;
no channel is free; 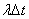 - the probability that in time
- the probability that in time 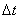 one application will come. We obtain the differential equation for
one application will come. We obtain the differential equation for 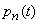 :
:
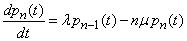 .
.
Thus, the obtained system of differential equations for probabilities 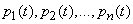 :
:
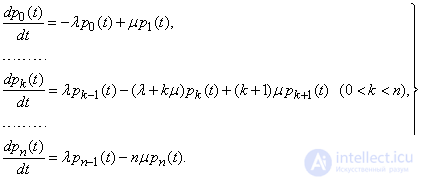 (19.8.8)
(19.8.8)
Equations (19.8.8) are called Erlang equations. Integration of the system of equations (19.8.8) with initial conditions
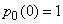 ;
; 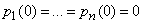
(at the initial moment all channels are free) gives dependence 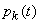 for anyone
for anyone 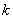 . Probabilities
. Probabilities 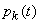 characterize the average load of the system and its change over time. In particular,
characterize the average load of the system and its change over time. In particular, 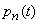 there is a possibility that the application that came at the moment
there is a possibility that the application that came at the moment 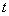 , will find all channels busy (will be rejected):
, will find all channels busy (will be rejected):
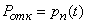 .
.
Magnitude 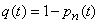 called relative system bandwidth. For the moment
called relative system bandwidth. For the moment 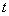 this is the ratio of the average number of applications served per unit of time to the average number of applications submitted.
this is the ratio of the average number of applications served per unit of time to the average number of applications submitted.
The system of linear differential equations (19.8.8) can be relatively easily integrated with any particular number of channels. 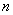 .
.
Note that in the derivation of equations (19.8.8) we never used the assumption that 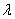 and
and 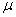 (density of application flow and release flow) are constant. Therefore, equations (19.8.8) remain valid for time-dependent
(density of application flow and release flow) are constant. Therefore, equations (19.8.8) remain valid for time-dependent 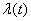 ,
, 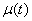 as long as the streams of events that translate the system from state to state remain Poissonian (without this, the process will not be Markovian).
as long as the streams of events that translate the system from state to state remain Poissonian (without this, the process will not be Markovian).
Comments
To leave a comment
Queuing theory
Terms: Queuing theory