19.11. Mixed type system with limited queue length

In the previous we considered a queuing system with a time limit in the queue. Here we consider a mixed-type system with a different kind of restriction of expectations - according to the number of applications queuing. Suppose that an application that has made all channels busy is queued only if it has less than 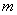applications; if the number of applications in the queue is 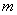(more 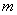it can not be), then the last arrived application in the queue does not become and leaves the system unserved. The remaining assumptions about the simplest flow of applications and the exponential distribution of the service time will remain the same.

So, there is 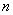-channel system with the expectation in which the number of applications queuing is limited by the number 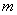. We construct differential equations for the probabilities of the states of the system. Note that in this case the number of system states will be finite, since the total number of applications associated with the system cannot exceed 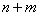( 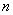serviced and 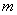standing in line). We list the system state:

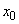- all channels are free, there is no queue,

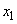- one channel is busy, there is no queue,

………

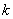- busy channels, no queues,

………

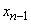- busy 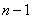channels, no queues,

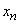- all busy 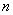channels, no queues,

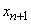- all busy 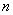channels, one application is in the queue,

………

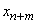- all busy 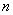channels, 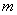applications standing in line.

Obviously, the first 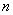equations for probabilities 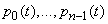will coincide with the Erlang equations (19.8.8). We derive the remaining equations. We have

,

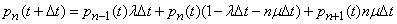from where

.

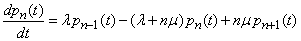Next, we derive the equation for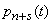

,

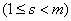
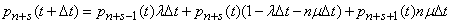from where

.

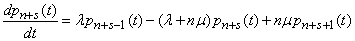The last equation will be

.

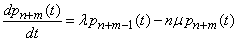Thus, the resulting system 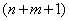differential equations:

(19.11.1)

Consider the limiting case of 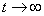. Equating all derivatives to zero, and considering all the probabilities constant, we obtain a system of algebraic equations

(19.11.2)

and additional condition:

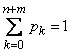. (19.11.3)

Equations (19.11.2) can be solved in the same way as we solved similar algebraic equations in previous 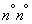. Without dwelling on this solution, we present only the final formulas:

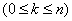, (19.11.4)

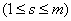. (19.11.5)

The probability that an application will leave the system unattended is equal to 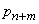of what is in line already 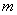applications.

It is easy to see that formulas (19.11.4) and (19.11.5) are obtained from formulas (19.10.11), (19.10.12), if we put in them 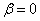and limit the summation by 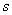upper boundary .

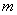Example. The simplest order flow arrives at the vehicle maintenance station with a density of 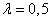(cars per hour). There is one room for repair. In the courtyard of the station can be at the same time, waiting for the queue, no more than three cars. Average time to repair one machine 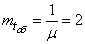(hours) Determine: a) system bandwidth; b) average station downtime; c) determine how these characteristics will change if you equip a second room for repair.

Decision. We have: , , , .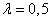

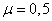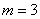a) According to the formula (19.11.5), assuming 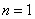, we find the probability that the incoming request will leave the system unattended:

.

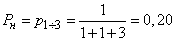Relative system bandwidth 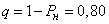. Absolute bandwidth: 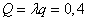(cars per hour).

b) The average proportion of time that the system will stand idle will be found by the formula (19.11.4): .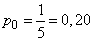

c) Believing 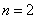, we will find:

,

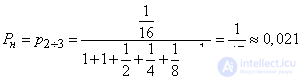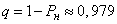(i.e. about 98% of all applications will be satisfied).

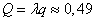(cars per hour).

Relative downtime: 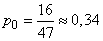i.e. the equipment will stand idle for about 34% of the total time.