The module r and the argument φ can be viewed as the polar coordinates a = r * cosφ, b = r * sin φ. Then from the algebraic notation of a complex number we can go to the trigonometric one:
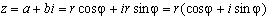
If complex numbers are given in trigonometric form, then the product and the particular numbers can be found as follows:

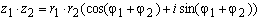
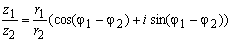

Multiplication of complex numbers has the following geometric meaning: if some complex number z1 = r1 (cos φ1 + isin φ1) corresponds to the vector OM1, and another complex number z2 = r2 (cos φ2 + isin φ2) corresponds to OM2, then the product z1 * z2 = r1 * r2 (cos (φ1 + φ2) + isin (φ1 + φ2)) corresponds to the vector OM, obtained from the vector OM1 by turning the angle φ2 and stretching r2 times for r2 ≥ 1 or compressing 1 / r2 for 0 <r2 <1 .
The division operation of complex numbers can also be interpreted geometrically as a combination of rotation and compression: now let the complex number z1 = r1 (cos φ1 + isin φ1) be OM1, and the other complex number z2 = r2 (cos φ2 + isin φ2) OM2 , then it can be argued that the vector OM, which is obtained from the vector OM1 by turning the angle φ2 in the negative direction and compressing r2 times for r2 ≥1 or stretching 1 / r2 at 0 <r2 <1, corresponds to the partial division of z1 / z2.
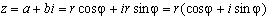

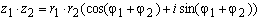
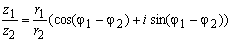

Comments
To leave a comment
Algebra
Terms: Algebra