Raising a complex number to a power - example

Let given a complex number. For the construction of a complex number in the natural degree, it is necessary to raise its module to this degree, and multiply the argument by the exponent. This rule is known in mathematics as the formula of Moivre:

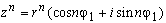
Raising to a natural power n, if it is large enough, complex numbers are easiest in trigonometric form, that is, if the number z = a + bi is given in algebraic form, then it must initially be written in trigonometric form.

Let the number z = | z | (cosϕ + isinϕ), then multiplying it by itself n times (which is equivalent to raising it to the power n), we get:

zn = (| z | (cosϕ + isinϕ)) n = | z | n (cosnϕ + isinnϕ)
Thus, the modulus of a complex number is equal to the same exponent of the modulus of the base, and the argument is equal to the argument of the base multiplied by the exponent.

If | z | = 1, then we obtain that

zn = (cosϕ + isinϕ) n = cosnϕ + isinnϕ
This formula is called the Moivre formula (Abraham de Moivre (1667 - 1754) - English mathematician).

What is the purpose of complex numbers and operations on them?
Answer: used in some areas of science.
In physics in quantum mechanics there is such a thing as a wave function, which itself is complex-valued.
In electrical engineering, complex numbers have found themselves as a convenient replacement for difura, which inevitably arise when solving problems with linear AC circuits.
The Zhukovsky theorem (wing lift) also uses complex numbers.
And also in biology, medicine, economics and many other places.

example