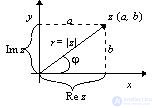
Consider the Cartesian coordinate system x0y. Let a point z (a; b) be assigned to each number z = a + bi. Such a plane is called complex. In other words, with each point z of this plane, a radius vector is determined, which determines the position of this point. The angle between the positive direction of the 0x axis and the radius vector counted in the counterclockwise direction is called the argument.
The 0x axis is called the real axis of the complex plane.
The 0y axis is called the imaginary axis of the complex plane.
The argument can take values in the interval -∞ <arg z <∞. The smallest absolute value of the argument is called the main one and is denoted by arg z = φ.
From the figure it follows that:
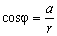
,
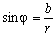
,
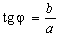
To find the argument, it is necessary to consider in which quarter of the complex plane is the number:
- I quadrant φ1 = arg z1 = φ;
- II quadrant φ1 = arg z1 = π - φ;
- III quadrant φ1 = arg z1 = π + φ;
- IV quadrant φ1 = arg z1 = 2π - φ; .
Find the module and the argument of the complex number:
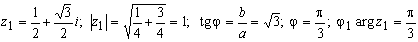
since z1 ∈ I quadrant.

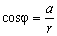 ,
, 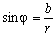 ,
, 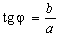
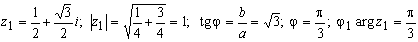
Comments
To leave a comment
Algebra
Terms: Algebra