Quaternions (from Lat. Quaterni , four each ) - a system of hypercomplex numbers that forms a vector space of four dimensions over the field of real numbers. Usually denoted by 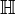. Offered by William Hamilton in 1843.

Quaternions are convenient for describing isometries of three- and four-dimensional Euclidean spaces, and therefore they are widely used in mechanics. They are also used in computational mathematics, for example, when creating three-dimensional graphics. ^[one]

Henri Poincare wrote about quaternions: “Their appearance gave a powerful impetus to the development of algebra; proceeding from them, science has taken the path of generalizing the concept of number, having come to the concepts of a matrix and a linear operator that permeates modern mathematics. It was a revolution in arithmetic, similar to that which Lobachevsky made in geometry ” ^[2] .

Definitions

Standard

Quaternions can be defined as a formal sum. 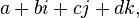Where 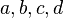- real numbers, and 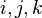- imaginary units with the following property: 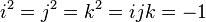. Thus, the base quaternion multiplication table is - looks like that:

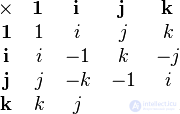
For example, 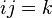a .

Like vector and scalar

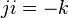Quaternion is a pair 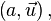Where 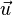- vector of three-dimensional space, and 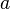- scalar, that is, a real number.

The addition operations are defined as follows:

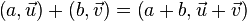
The product is defined as follows:

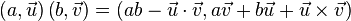
Where denotes the scalar product, and 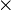- vector product.

In particular,

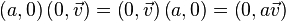
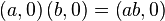
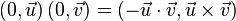
Notice, that:

• Algebraic operations in quaternions have the property of distributivity;
• The anticommutativity of a vector product implies the noncommutativity of the product of quaternions.

Through complex numbers

Arbitrary quaternion 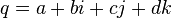can be represented as a pair of complex numbers in the form

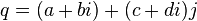
or equivalent

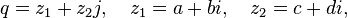
Where 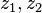- complex numbers, since 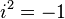performed for both complex numbers and quaternions, and .

Through matrix representations

Real matrices

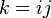Quaternions can also be defined as real matrices of the following form with the usual matrix product and sum:

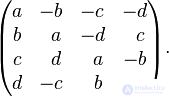
With this entry:

• the transposed matrix corresponds to the conjugate quaternion:

  ;

• the fourth power of the quaternion modulus is equal to the determinant of the corresponding matrix:

  .

Complex matrices

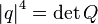Alternatively, quaternions can be defined as complex matrices of the following form with the usual matrix product and sum:

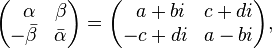
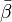here and denote complex conjugate numbers to 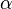and .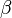

This view has several remarkable properties:

• a complex number corresponds to a diagonal matrix;
• the conjugate quaternion corresponds to the conjugate transposed matrix:

  ;

• the square of the quaternion module is equal to the determinant of the corresponding matrix:

  .

Related objects and operations

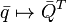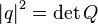For quaternion

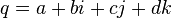
quaternion 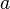called the scalar part 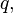and quaternion 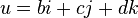- vector part . If a 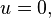then the quaternion is called purely scalar , and if 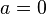- purely vector .

Pairing

For quaternion 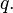is called conjugate :

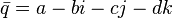
The conjugate product is the product of the conjugate in the reverse order:

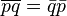
For quaternions equality

Module

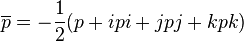
Just like for complex numbers,

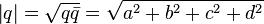
called module 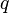. If a 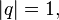that 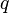called a single quaternion .

As a norm of a quaternion, its module is usually considered: .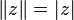

Thus, a metric can be introduced on a set of quaternions. Quaternions form a metric space isomorphic 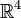with a Euclidean metric.

Quaternions with a module as a norm form a Banach algebra.

The identity of the four squares implies that 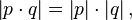in other words, quaternions possess a multiplicative norm and form an associative division algebra.

Inversion of multiplication (division)

Quaternion, inverse to multiplication 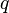It is calculated as: .

Algebraic properties

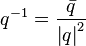Four basic quaternions and four opposite in their sign form, by multiplication, a group of quaternions (about 8). Denoted by:

.

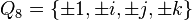Quaternion multitude is an example of a split ring.

The set of quaternions forms a four-dimensional associative division algebra over the field of real (but not complex) numbers. At all , , are the only finite-dimensional associative division algebras over the field of real numbers ^[3] .

The noncommutativity of multiplication of quaternions leads to unexpected consequences. For example, the number of different roots of a polynomial equation over a set of quaternions may be greater than the degree of the equation. In particular, the equation 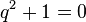It has infinitely many solutions - these are all single, purely vector quaternions.

Quaternions and turns of space

The organization of the three degrees of freedom, but the final freedom of the smaller rings depends on the position of the larger rings.

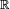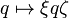Quaternions considered as algebra over , form a four-dimensional real vector space. Any turn of this space is relatively can be written as where 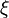and 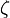- a pair of single quaternions, with a pair 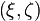is determined to within a sign, that is, one turn determines exactly two pairs - 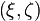and . From this it follows that the Lie group 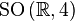turns there is a factor group 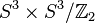where denotes the multiplicative group of unit quaternions.

Pure vector quaternions form a three-dimensional real vector space. Any rotation of the space of purely vector quaternions with respect to 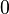can be written as 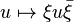where 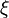- some unit quaternion. Respectively, 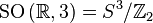, in particular, 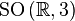diffeomorphic .

"Whole" Quaternions

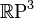As the norm of a quaternion, choose the square of its module: .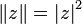

Whole by Hurwitz (also engl) is called quaternions such that all 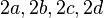- integers and the same parity.

A whole quaternion is called

• even
• odd
• simple

if its property has the same property.

A whole quaternion is called primitive if it is not divisible by any positive number except 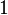, of course (in other words, ).

Whole unit quaternions

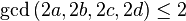There are 24 whole unit quaternions:

, , , ,

.

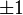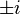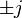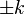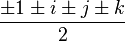They form a group by multiplication and lie at the vertices of a regular four-dimensional polyhedron - a cuboctahedron (not to be confused with a three-dimensional polytope-cubooctahedron).

Simple factorization

For primitive quaternions, an analogue of the main theorem of arithmetic is true.

Theorem. ^[4] For any fixed order of factors in the expansion of the quaternion norm 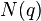into the product of simple positive integers 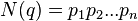there is a quaternion decomposition 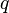into a product of simple quaternions 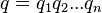such that 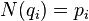. Moreover, this decomposition is only modulo the unit multiplication, which means that any other decomposition will have the form

,

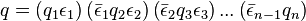Where 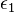, , 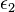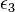... 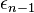- whole unit quaternions.

For example, primitive quaternion 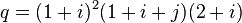has a rate of 60, so, modulo multiplication by one, it has exactly 12 expansions into the product of simple quaternions, corresponding to 12 expansions of the number 60 in simple products:

The total number of expansions of such a quaternion is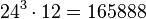

Quaternion variable functions

Secondary functions

The quaternion sign is calculated as follows:

.

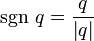The quaternion argument is the rotation angle of the four-dimensional vector, which is measured from the real unit:

.

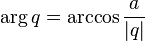Subsequently, the representation of the given quaternion is used. 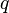as

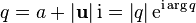
Here 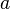- the real part of the quaternion, 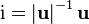. Wherein 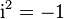which is why passing through 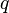and the real straight plane has the structure of an algebra of complex numbers, which makes it possible to transfer arbitrary analytic functions to the case of quaternions. They satisfy standard relations if all arguments are 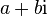for a fixed unit vector 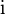. If it is necessary to consider quaternions with different directions, the formulas become much more complicated, due to the noncommutativity of the quaternion algebra.

Elementary functions

The standard definition of analytic functions on associative normalized algebra is based on the expansion of these functions into power series. The arguments proving the correctness of the definition of such functions are completely analogous to the complex case and are based on the calculation of the radius of convergence of the corresponding power series. Given the above “complex” representation for a given quaternion, the corresponding series can be reduced to the following compact form. Here are just some of the most commonly used analytic functions, and you can calculate any analytic function in the same way. The general rule is: if 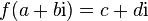for complex numbers then 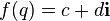where quaternion 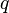considered in the "integrated" view .

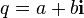Degree and logarithm

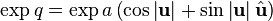
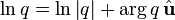
Note that, as usual in complex analysis, the logarithm is determined only up to .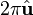

Trigonometric functions

Regular functions

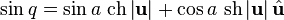
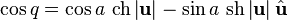
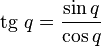
There are various ways to define regular functions of a quaternion variable. The most obvious one is the consideration of quaternionally differentiable functions, while one can consider right-differentiable and left-differentiable functions that do not coincide due to non-commutativity of multiplication of quaternions. Obviously, their theory is completely similar. Define a quaternion-left-differentiable function 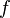as having a limit

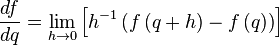
It turns out that all such functions have in some neighborhood of the point 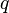view

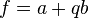
Where - permanent quaternions. Another method is based on the use of operators.

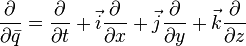
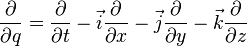
and consideration of such quaternion functions 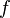for which ^[5]

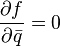
which is completely analogous to using operators 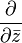and 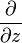in a complex case. In this case, analogs of the Cauchy integral theorem, the theory of residues, harmonic functions, and Laurent series for quaternion functions are obtained ^[6] .

Derivative gato

The Gato derivative of the function of the quaternion variable is determined according to the formula

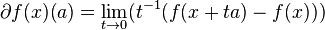
Gato's derivative is an additive mapping of the increment of the argument and can be represented as ^[7]

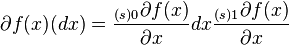
Here we assume summation over the index . The number of items depends on the choice of function. 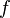. Expressions 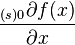and 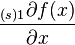are called derivative components.

Types of multiplications

Grassmann multiplication

So differently called the common multiplication of quaternions ( ).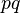

Euclidean multiplication

It differs from the generally accepted fact that instead of the first factor, the conjugate to it is taken: 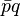. It is also non-commutative.

Scalar product

Similar to the operation of the same name for vectors:

.

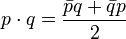This operation can be used to highlight one of the coefficients, for example, .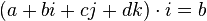

The definition of a quaternion module can be modified:

.

External product

.

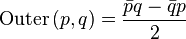It is used not very often, however it is considered in addition to the scalar product.

Vector product

Similar to the operation of the same name for vectors. The result is also a vector:

.

From the history

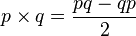Memorial plaque on the Broome Bridge in Dublin: “Sir William Rowan Hamilton opened the formula for multiplication of quaternions on a walk on October 16, 1843, in a flash of genius, ^[8]

Система кватернионов была впервые опубликована Гамильтоном в 1843 году. Историки науки также обнаружили наброски по этой теме в неопубликованных рукописях Гаусса, относящихся к 1819—1820 годам. ^[9]

Бурное и чрезвычайно плодотворное развитие комплексного анализа в XIX веке стимулировало у математиков интерес к следующей задаче: найти новый вид чисел, аналогичный по свойствам комплексным, но содержащий не одну, а две мнимые единицы. Предполагалось, что такая модель будет полезна при решении пространственных задач математической физики. Однако работа в этом направлении оказалась безуспешной.

A new kind of numbers was discovered by the Irish mathematician William Hamilton in 1843, and it contained not two, as expected, but three imaginary units. Hamilton called these numbers quaternions . Later, Frobenius strictly proved (1877) a theorem, according to which it is impossible to extend a complex field to a field or body with two imaginary units.

Despite the unusual properties of the new numbers (their noncommutativity), this model quickly brought practical benefits. Maxwell used the compact quaternion notation to formulate his own electromagnetic field equations. ^[10] Later, a three-dimensional vector analysis (Gibbs, Heaviside) was created based on quaternion algebra.

Modern application

In the 20th century, several attempts were made to use quaternion models in quantum mechanics ^[11] and the theory of relativity ^[12] . Quaternions have found a real use in modern computer graphics and programming of games ^[13] , as well as in computational mechanics ^{[14] [15]} , in inertial navigation and control theory ^{[16] [17]} . Since 2003, the journal “Hypercomplex Numbers in Geometry and Physics” has been published ^[18] .

In many applications, more general and practical means than quaternions have been found. For example, nowadays matrix calculus is most often used to study movements in space ^[19] . However, where it is important to specify a three-dimensional rotation using the minimum number of scalar parameters, the use of Rodrig – Hamilton parameters (that is, the four components of the quaternion of rotation) is often preferred: this description never degenerates, and when describing turns with three parameters (for example, Euler angles ) there are always critical values ​​of these parameters when the description degenerates ^{[14] [15]} .

Like algebra over 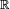, quaternions form real vector space 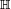equipped with a third-rank tensor 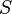of type (1,2), sometimes called the structure tensor . Like any kind of tensor 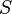displays each 1-form 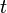on 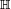and a couple of vectors 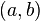of 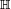in real number 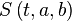. For any fixed 1-form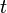 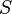turns into a covariant second-rank tensor, which, in the case of its symmetry, becomes a scalar product on 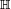. Since each real vector space is also a real linear manifold, such a scalar product generates a tensor field, which, under the condition of its nondegeneracy, becomes the (pseudo- or proper) Euclidean metric on 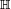. In the case of quaternions, this scalar product is indefinite, its signature does not depend on the 1-form 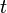, and the corresponding pseudo-Euclidean metric is the Minkowski metric ^[20] . This metric automatically extends to the Lie group of nonzero quaternions along its left-invariant vector fields, forming the so-called closed FLRU (Friedman - Lemetr - Robertson - Walker) metric ^[21] - an important solution to the Einstein equations. These results clarify some aspects of the compatibility problem of quantum mechanics and the general theory of relativity within the framework of the theory of quantum gravity ^[22] .

see also

• Quaternions and space rotation
• Quaternion analysis
• Octave
• Frobenius theorem
• Articulated wedge

Quaternions in game programming.

There are several ways to represent the rotation of objects. Many programmers use for this matrix rotation or Euler angles. Each of these solutions works fine, as long as you do not try to implement a smooth interpolation between two different positions of the object. For example, imagine an object that simply rotates freely in space. If you store the rotation as a matrix or in the form of Euler angles, then smooth interpolation will be quite expensive in calculations and will not be as smooth as in interpolation by quaternions. Although it is possible to try to place the temporary keys most closely at the stage of creating the animation, however, this entails storing more data for a given rotation and it is not quite trivial to know which step to choose. It is clear that in this case one cannot do without interpolation, one never knows which FPS the player will have.

Many third-person games use quaternions to animate camera motion. All third-person games place the camera at some distance from the character. Since the camera has a different movement, different from the movement of the character, for example, when you rotate the character - the camera moves in an arc, it sometimes happens that this movement does not look natural, irregular. This is one of the problems that can be solved using quaternions. Quaternions are also convenient to use in flight simulators, such as the IL-2 Sturmovik. Instead of manipulating the three corners (roll, pitch, and yaw), representing rotation around the x, y, and z axes, respectively, it is much easier to use one quaternion. And in general, many games and applications of three-dimensional graphics retain the orientation of objects in quaternions. For example, it is easier to add angular velocity to the quaternion than to the matrix.

What it is
Basic operations and properties of quaternions
Transformations
Rotation around axis
Transformation of spherical coordinates to quaternion
Euler angles
Conversion of the rotation matrix into quaternion
Converting a single quaternion into a rotation matrix
Smooth interpolation
Quaternions in DirectX
Quaternions in the MAX SDK
Related Links

What it is?

Quaternions were introduced by Hamilton in the 18th century. Quaternions are a 4-dimensional extension of the set of complex numbers; in other words, they are hypercomplex numbers. That is, the quaternion q is defined by a foursome of numbers (x, y, z, w):

w + xi + yj + zk
where i ² = j ² = k ² = –1.

It can also be written in the form:

[w, v]
where w is the scalar, and v = (x, y, z) is the vector.

Basic operations and properties of quaternions

Consider two quaternions: q [w, v] and q '[w', v ']. For them, the following is true:

q + q '= [w + w', v + v ']

qq '= [ww' - v · v ', vxv' + wv '+ w'v]
where x is a vector product and · is a scalar.

norm (q) = sqrt (w ² + x ² + y ² + z ² ) (size)

q * = [w, –v] (conjugation)

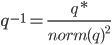
norm (q) = 1 => q ^–1 = q *

Quaternions expand the concept of rotation in three-dimensional space to rotation in four-dimensional. Rotation can be given by a single quaternion (norm (q) = 1). To bring a quaternion to a single form, or in other words to normalize, it is necessary to calculate its size norm (q) and divide all four members of the quaternion by the value of the size obtained.

Quaternion space is a 4-dimensional space. The set of all unit vectors is a 4-dimensional sphere with a radius of 1. Quaternions can be considered as adding an additional angle of rotation to spherical coordinates, (spherical coordinates are longitude, latitude, angle of rotation).

If the rotation is given by some quaternion q, then the vector v after rotation will have the form v ':

V '= q V q ^–1
where V = [o, v], V '= [0, v']

Transformations

Rotation around axis

Consider rotation by an angle Q around the axis defined by the guiding vector v. This rotation can be set by quaternion:
q = [cos (Q / 2), sin (Q / 2) v]

If necessary, you need to remember to normalize the resulting quaternion.

Transformation of spherical coordinates into quaternion

  struct Quaternion {
   float x, y, z;  // Vector
   float w;  // Scalar
 };

 // Transformation of spherical coordinates to quaternion
 void SphericalToQuaternion (Quaternion * q, float latitude, float longitude, 
                            float angle)
 {
   float sin_a = sin (angle / 2);
   float cos_a = cos (angle / 2);

   float sin_lat = sin (latitude);
   float cos_lat = cos (latitude);

   float sin_long = sin (longitude);
   float cos_long = cos (longitude);

   q-> x = sin_a * cos_lat * sin_long;
   q-> y = sin_a * sin_lat;
   q-> z = sin_a * sin_lat * cos_long;
   q-> w = cos_a;
 } 

Euler angles

Rotation is given by yaw, pitch and roll. Then the quaternion is calculated as follows:

qroll = [cos (y / 2), (sin (y / 2), 0, 0)]
qpitch = [cos (q / 2), (0, sin (q / 2), 0)]
qyaw = [cos (f / 2), (0, 0, sin (f / 2))]
q = qyaw qpitch qroll

Conversion of the rotation matrix into quaternion

To set the rotation, a 3x3 matrix is ​​enough. However, since many 3D APIs are used to transform a 4x4 matrix, we will also consider such a dimension of the matrix. At the same time, in order for the additional data not to affect the meaning of the matrix, the additional row and column are set to zero, with the exception of their intersection, which is set to 1. Below is the conversion code of the rotation matrix into a quaternion. It is clear that this matrix should not carry any other information besides rotation, for example, scaling.

  // Matrix to Quaternion Transformation
 void MatrixToQuaternion (Quaternion * quat, float m [4] [4])
 {
   float tr, s, q [4];
   int i, j, k;

   int nxt [3] = {1, 2, 0};

   tr = m [0] [0] + m [1] [1] + m [2] [2];

   if (tr> 0.0)
   {
     s = sqrt (tr + 1.0);
     quat-> w = s / 2.0;
     s = 0.5 / s;
     quat-> x = (m [1] [2] - m [2] [1]) * s;
     quat-> y = (m [2] [0] - m [0] [2]) * s;
     quat-> z = (m [0] [1] - m [1] [0]) * s;
   }
   else
   {
     i = 0;
     if (m [1] [1]> m [0] [0]) i = 1;
     if (m [2] [2]> m [i] [i]) i = 2;
     j = nxt [i];
     k = nxt [j];

     s = sqrt ((m [i] [i] - (m [j] [j] + m [k] [k])) + 1.0);

     q [i] = s * 0.5;

     if (s! = 0.0) s = 0.5 / s;

     q [3] = (m [j] [k] - m [k] [j]) * s;
     q [j] = (m [i] [j] + m [j] [i]) * s;
     q [k] = (m [i] [k] + m [k] [i]) * s;

     quat-> x = q [0];
     quat-> y = q [1];
     quat-> z = q [2];
     quat-> w = q [3];
   }
 } 

Converting a single quaternion into a rotation matrix

The transformation of a single quaternion into a rotation matrix can be written as:

TRot = [1-2y2-2z2 2xy-2wz 2xz + 2wy
2xy + 2wz ​​1-2x2-2z2 2yz-2wx
2xz-2wy 2yz + 2wx 1-2x2-2y2]

  // Convert Quaternion To Matrix
 void QuaternionToMatrix (float m [4] [4], const Quaternion * quat)
 {
   float wx, wy, wz, xx, yy, yz, xy, xz, zz, x2, y2, z2;
   x2 = quat-> x + quat-> x;
   y2 = quat-> y + quat-> y;
   z2 = quat-> z + quat-> z;
   xx = quat-> x * x2;  xy = quat-> x * y2;  xz = quat-> x * z2;
   yy = quat-> y * y2;  yz = quat-> y * z2;  zz = quat-> z * z2;
   wx = quat-> w * x2;  wy = quat-> w * y2;  wz = quat-> w * z2;

   m [0] [0] = 1.0f- (yy + zz);  m [0] [1] = xy-wz;  m [0] [2] = xz + wy;
   m [1] [0] = xy + wz;  m [1] [1] = 1.0f- (xx + zz);  m [1] [2] = yz-wx;
   m [2] [0] = xz-wy;  m [2] [1] = yz + wx;  m [2] [2] = 1.0f- (xx + yy);

   m [0] [3] = m [1] [3] = m [2] [3] = 0;
   m [3] [0] = m [3] [1] = m [3] [2] = 0;
   m [3] [3] = 1;
 } 

When working with a hierarchy of objects and inverse kinematics, a composite task of rotation arises. In this case, the use of quaternions is preferable to matrices. That is, if the rotation is given by two matrices R1 and R2, then in order to calculate the rotation matrix, these matrices must be multiplied: R = R1 x R2. Similarly, if the rotation is given by two quaternions q1 and q2, then the resulting rotation quaternion will be q = q1 x q2. It is clear that the calculation of the product of quaternions is faster than matrices. Moreover, the product of quaternions can be optimized:

  void MulQuaternions (Quaternion * res, 
                     const Quaternion * q1, const Quaternion * q2)
 {
   float A, B, C, D, E, F, G, H;

   A = (q1-> w + q1-> x) * (q2-> w + q2-> x);
   B = (q1-> z - q1-> y) * (q2-> y - q2-> z);
   C = (q1-> x - q1-> w) * (q2-> y + q2-> z);
   D = (q1-> y + q1-> z) * (q2-> x - q2-> w);
   E = (q1-> x + q1-> z) * (q2-> x + q2-> y);
   F = (q1-> x - q1-> z) * (q2-> x - q2-> y);
   G = (q1-> w + q1-> y) * (q2-> w - q2-> z);
   H = (q1-> w - q1-> y) * (q2-> w + q2-> z);

   res-> w = B + (-E - F + G + H) * 0.5;
   res-> x = A - (E + F + G + H) * 0.5; 
   res-> y = -C + (E - F + G - H) * 0.5;
   res-> z = -D + (E - F - G + H) * 0.5;
 } 

  void Slerp (Quaternion * res
            Quaternion * q, Quaternion * p, float t)
 {
   float p1 [4];
   double omega, cosom, sinom, scale0, scale1;

   // cosine of an angle
   cosom = q-> x * p-> x + q-> y * p-> y + q-> z * p-> z + q-> w * p-> w;

   if (cosom <0.0)
   { 
     cosom = -cosom;
     p1 [0] = - p-> x;  p1 [1] = - p-> y;
     p1 [2] = - p-> z;  p1 [3] = - p-> w;
   }
   else
   {
     p1 [0] = p-> x;  p1 [1] = p-> y;
     p1 [2] = p-> z;  p1 [3] = p-> w;
   }

   if ((1.0 - cosom)> DELTA)
   {
     // standard case (slerp)
     omega = acos (cosom);
     sinom = sin (omega);
     scale0 = sin ((1.0 - t) * omega) / sinom;
     scale1 = sin (t * omega) / sinom;
   }
   else
   {        
     // if a small angle - linear interpolation
     scale0 = 1.0 - t;
     scale1 = t;
   }

   res-> x = scale0 * q-> x + scale1 * p1 [0];
   res-> y = scale0 * q-> y + scale1 * p1 [1];
   res-> z = scale0 * q-> z + scale1 * p1 [2];
   res-> w = scale0 * q-> w + scale1 * p1 [3];
 } 

  typedef struct D3DXQUATERNION {
   FLOAT x, y, z, w;
 } D3DXQUATERNION; 

  void GetQuat (Quat * pQuat, const pNode * pNode)
 {
   Control * pTransf = pNode-> GetTMController ();
   if (pTransf)
   {
     Control * pCtrl = pTransf-> GetRotationController ();
     if (pCtrl)
       pCtrl-> GetValue (0, pQuat, NEVER, CTRL_ABSOLUTE);
   }
 } 

  dx_quat.x = -max_quat.x;
 dx_quat.y = -max_quat.z;
 dx_quat.z = -max_quat.y;
 dx_quat.w = max_quat.w;