Lecture
The Käli algebra is a system of hypercomplex numbers, an 8-dimensional algebra over the field of real numbers. Usually denoted by 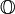 , because its elements ( Cayley numbers ) are sometimes called octonions or octaves .
, because its elements ( Cayley numbers ) are sometimes called octonions or octaves .
Cayley number is a linear combination of elements. 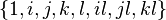 . Each octave x can be written in the form
. Each octave x can be written in the form
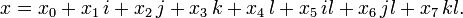
with real coefficients 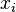 . Octonions are used in physics: for example, in STR and string theory [1] . Octave multiplication table:
. Octonions are used in physics: for example, in STR and string theory [1] . Octave multiplication table:
| one | i ( e1 ) | j ( e2 ) | k ( e3 ) | l ( e4 ) | il ( e5 ) | jl ( e6 ) | kl ( e7 ) |
|---|---|---|---|---|---|---|---|
| i ( e1 ) | −1 | k | - j | il | - l | - kl | jl |
| j ( e2 ) | - k | −1 | i | jl | kl | - l | - il |
| k ( e3 ) | j | - i | −1 | kl | - jl | il | - l |
| l ( e4 ) | - il | - jl | - kl | −1 | i | j | k |
| il ( e5 ) | l | - kl | jl | - i | −1 | - k | j |
| jl ( e6 ) | kl | l | - il | - j | k | −1 | - i |
| kl ( e7 ) | - jl | il | l | - k | - j | i | −1 |
Table (Cayley) octonion multiplication [2]
| e 0 | e 1 | e 2 | e 3 | e 4 | e 5 | e 6 | e 7 |
|---|---|---|---|---|---|---|---|
| e 1 | -one | e 3 | −e 2 | e 5 | −e 4 | −e 7 | e 6 |
| e 2 | −e 3 | -one | e 1 | e 6 | e 7 | −e 4 | −e 5 |
| e 3 | e 2 | −e 1 | -one | e 7 | −e 6 | e 5 | −e 4 |
| e 4 | −e 5 | −e 6 | −e 7 | -one | e 1 | e 2 | e 3 |
| e 5 | e 4 | −e 7 | e 6 | −e 1 | -one | −e 3 | e 2 |
| e 6 | e 7 | e 4 | −e 5 | −e 2 | e 3 | -one | −e 1 |
| e 7 | −e 6 | e 5 | e 4 | −e 3 | −e 2 | e 1 | -one |
Often numbers can be replaced by letter designation:
| Number | one | 2 | 3 | four | five | 6 | 7 |
| Letters | i | j | k | l | il | jl | kl |
| Replacement | i | j | k | l | m | n | o |
Let octonion be given
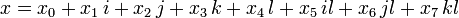
Octonion Pairing Operation 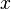 defined by equality
defined by equality
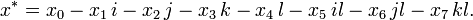
The conjugate operation satisfies the equalities.
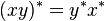
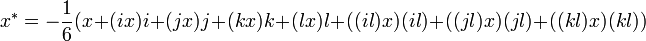
The real part of the Octonion 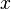 defined by equality
defined by equality
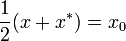
and the imaginary part of the Octonion 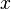 defined by equality
defined by equality
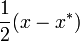
Norma Octonion 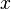 defined by equality
defined by equality
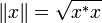 .
. It is easy to make sure that the norm is a non-negative real number
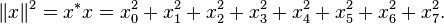
Consequently, 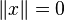 then and only if
then and only if 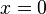 .
.
From the definition of the norm it follows that the octonion 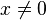 reversible and
reversible and
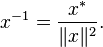
First considered in 1843 by Graves, Hamilton's friend [3] , and Cayley independently two years later.
Comments
To leave a comment
Algebra
Terms: Algebra