Hyperoperator

In mathematics, a hyperoperator is a generalization of traditional operators (the arithmetic operations of addition, multiplication, and exponentiation, considered as hyperoperators of the 1st, 2nd, and 3rd order, respectively) to higher orders. In general, due to non-commutativity, a hyperoperator has two inverse functions — a hyperroot (e.g., a Superroot for the 4th order) and a hyperlogarithm (Superlogarithm).

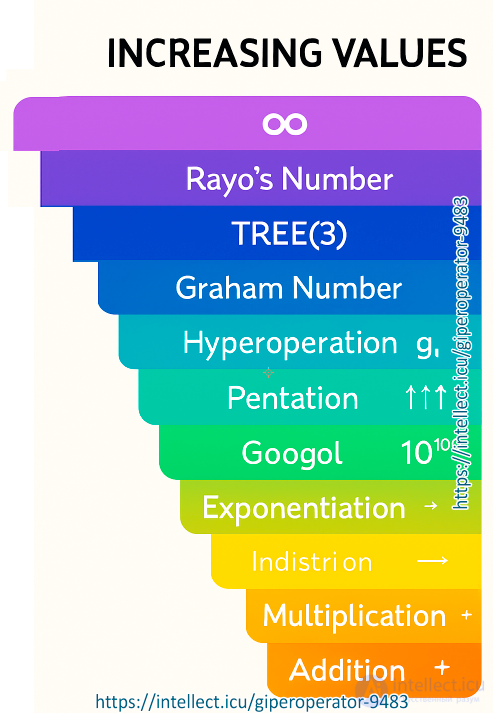
A hyperoperator is a general concept that covers a number of operations that are generalizations of elementary arithmetic operations (addition, multiplication, exponentiation, etc.). The basic sequence of hyperoperators begins with the following operations:

1. h₁(a, b) = a + b (addition),
2. h₂(a, b) = a × b (multiplication),
3. h₃(a, b) = a^b (raising to a power),
4. h₄(a, b) is tetration (repeated raising to a power),
5. h₅(a, b) is a pentation, and so on.

Each subsequent hyperoperator can be considered as a repetition of the previous one. For example, pentation is a repetition of tetration, where the value of the second argument is used as the exponent.

This sequence allows us to define higher-level operations that are used in mathematics to work with large numbers and for research in computational theory, recursive functions, and other disciplines.

Story

In 1928, David Hilbert's student, mathematician Wilhelm Ackermann, published as an example of a everywhere defined, non-primitive recursive computable function of three arguments , such that for it defined the operations of addition, multiplication, and exponentiation, respectively:

;

;

.

Since 1976, after the publication of Knuth's arrow notation, it has become possible to write the original Ackermann function in a more convenient form:

.

Besides its historical role as the first universally defined non-primitive recursive computable function, Ackermann's original function extended the basic arithmetic operations beyond exponentiation, although not as well as dedicated functions like Goodstein's hyperoperator sequence.

Definition

The order hyperoperator with arguments and (henceforth denoted as ) is recursively defined as the result of repeatedly applying the order hyperoperator to a sequence of identical arguments (starting with multiplication, each of which is ):

• addition and - increase of a number by a number of units equal to

• multiplication by - adding a number to itself times:
• raising a to the power b is multiplying a number by itself times
• 
• 

In the last expression, the operations are performed from right to left , which is significant because hyperoperators of order {\displaystyle n>2} are neither commutative nor associative. This is stated on the website https://intellect.icu . Hyperoperators of order 4, 5, and 6 are called "tetration", "pentation", and " hexation ", respectively.

In the simplest case, the values ​​of the variables , and {\displaystyle n} are limited to natural numbers. Possible generalizations of hyperoperators to arbitrary real or complex numbers have not yet been studied much.

Different mathematicians denote hyperoperators in different ways:

• Knut uses arrows ;
• Conway uses arrows .

As a result we get:

The generalization of the first three operations (addition, multiplication, raising to a power) in infix form is:

Then the hyperoperator is defined as

Let's write it out for the first four natural numbers n:

Inverse operations

As mentioned above, due to non-commutativity (in the general case), the hyperoperator has two inverse functions - the hyperroot and the hyperlogarithm.

Due to commutativity, the hyperroot and hyperlogarithm of addition coincide and together form the inverse operation of addition - subtraction.

In the same way, the inverse operations of multiplication coincide, forming one inverse operation of multiplication - division.

Already for raising to a power, the inverse functions become different (root and logarithm).

Inverse operations are generalized for hyperoperators of any order.

Alternative operations

Calculation from left to right

An alternative operation can be obtained by calculating from left to right and, due to the commutativity and associativity of the addition and multiplication operations, this operation coincides with the Hyperoperator at :

For a hyperoperator, the left-to-right computation (i.e. the alternative operation) differs from the hyperoperator and leads to a different result, for example, for we get the hyperoperator tetration : .

But calculating the power tower from left to right will lead to the wrong result: .

Application

The practical application of hyperoperators is limited to specific areas, since operations above exponentiation (e.g. tetration, pentation) quickly produce very large numbers that are difficult to handle. However, hyperoperators can be useful in some scientific and engineering fields:

1. Theory of Computation and Algorithm Complexity

Hyperoperators can be used to analyze algorithms with a very high degree of computational complexity. For example, some problems in theoretical computer science, such as computing large numbers or constructing computational circuits, require operations that can be described using hyperoperators.

2. Cryptography

Cryptography uses large numbers to create complex keys and ciphers. Exponentiation and other hyperoperators can play a role in creating more complex encryption schemes and data protection methods.

3. Astronomy and physics

In models where one must work with very large numbers (for example, estimates of the size of the universe or the lifetimes of objects), hyperoperators can be useful for conveniently representing such numbers.

4. Theoretical Mathematics

In mathematics, hyperoperators are used to study large numbers, such as Graham's number, which is related to the Ramsey problem. This number is too large to be written using ordinary powers, and hyperoperators allow us to describe it.

5. Numerical theories and combinatorics

In the field of number theory, especially when dealing with rapidly growing sequences, hyperoperators can be used to describe such functions and their properties.

Despite limited direct application in everyday computing, hyperoperators play an important role in theoretical research and in solving problems involving extremely large numbers.