Lecture
The transition and state tables are a programming method not only for tasks that are reduced to finite automata. When discussing the XML / XSL approach to the problem of standardized representation of transition tables, the possibilities of applying the operating method with structural representations of data and programs for a wider class of algorithms were indicated.
However, we have not yet solved the problem, when the presentation of the algorithm depends on the input data. It is classified for automata as a problem of dynamically generating an automaton (see  9.3, clause 3). Of course, from this angle you can consider the translation: a text file in the input language is a part of the data, generating a plan for processing another part of the data, which is presented when solving a specific task. The second task of this type, for which the methods are developed, is the task of specialization of the universal program. It can also be considered as a refinement of the general plan, based on a partial knowledge of the data being processed. The mentioned cases are characterized by the fact that the representation of the algorithm, depending on the part of the input data, is built from pre-defined blanks. For example, for translation, such blanks are algorithms for performing an abstract-syntactic representation of a program.
9.3, clause 3). Of course, from this angle you can consider the translation: a text file in the input language is a part of the data, generating a plan for processing another part of the data, which is presented when solving a specific task. The second task of this type, for which the methods are developed, is the task of specialization of the universal program. It can also be considered as a refinement of the general plan, based on a partial knowledge of the data being processed. The mentioned cases are characterized by the fact that the representation of the algorithm, depending on the part of the input data, is built from pre-defined blanks. For example, for translation, such blanks are algorithms for performing an abstract-syntactic representation of a program.
This section shows a different method for constructing an algorithm that depends on the input data. His idea is to create a representation of the algorithm that allows for direct interpretation. The natural way to demonstrate the method is to take as a basis a well-known class of algorithms, a specific representative of which is selected based on the knowledge of the input data.
Let us turn to the problem, which is solved for each specific case using a special type of finite automaton (as always, the choice of a specific representation significantly affects the complexity and other characteristics of the program; automatic application of previously used representations in other tasks is not recommended).
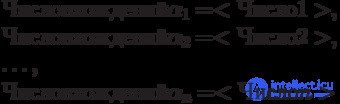
Suppose you want to count how many times each of the input words is found in some large file (now the word is any sequence of characters).  - words entered;
- words entered; 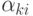 - the word. Type:
- the word. Type:
Where is the total number of occurrences of the word 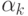 in the file, taking into account the possible overlap of words (for example, in the line * MOM = {} two occurrences of the word MOM)
in the file, taking into account the possible overlap of words (for example, in the line * MOM = {} two occurrences of the word MOM)
For words defined in advance, it is easy to construct a graph, each vertex of which represents characters inside words. Its vertices are marked with a symbol. Two arcs emanate from such a vertex: the first points to the vertex to which it should go when the next readable symbol coincides with the vertex mark, and the second to the one that should become the successor given in case of a mismatch. It is easy to see that this is one of the forms of representation of a finite automaton, each state of which encodes the set of all vertices connected by arcs of the second type, and the successor states are determined by arcs of the first type of the original graph. In order for this machine to work (solved the task), you need to provide it with actions that reduce to an increase in the counters corresponding to the words found, as well as determine the initial and final states. We will not alter the original graph, since such its form is more convenient for interpretation.
If the arcs of the first type are represented by arrows emanating in the horizontal direction, the arcs of the second type are shown by vertical arrows, and actions with counters are indicated by corresponding marks for arcs, then, for example, for a set of words
the graph shown in fig. 12.1.
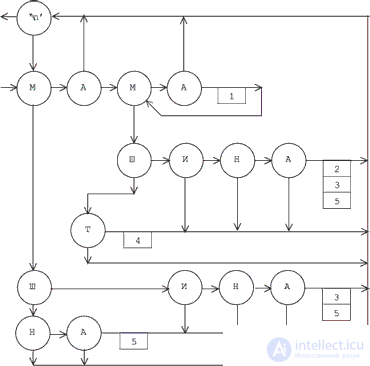
For our example, the automaton graph is represented by the following table (transition 111, indicating beyond the table, is used to indicate that the file has been viewed):
1) MOM, 2) MACHINE, 3) BUS, 4) MAT, 5) ON. 1) MOM, 2) MACHINE, 3) BUS, 4) MAT, 5) ON. 0. '\ n' 111 1 1. M 2 15 2. A 3 0 3. M 4 6 4. A 5 0 5. <1> 3 - 6. W 7 14 7. And 8 0 8. N 9 0 9. A 10 0 10. <2> 11 - 11. <3> 12 - 12. <5> 1 - 13. T 14 0 14. <4> 1 - 15. Ø 16 19 16. And 17 0 17. N 18 0 18. A 11 0 19. N 20 0 20. A 12 0 21.
0 -
The graph interpretation program is simple, and for this problem it makes no sense to use a translational implementation of operating with a table. Operators Current_Reaction (); and Final_Reaction (); used to indicate actions with counters, for example, those that are given in the comments.
s = getchar ();
i = 1;
for (;;) {
if (Table [i] .Tag) {
if (Table [i] .Symb == s) {
i = Table [i] .yes; // next line
if (s! = '\ n')
s = getchar ();
else return;
}
else
i = Table [i] .no; // next line
}
else {
Current_Reaction (); // M [Table [i] .Num] ++
i = Table [i] .yes; // next line
}
}
Final_Reaction (); // Listing M
Listing 12.1.4.In this interpreter, the data structure does not contain descriptions of actions - they are only identified by the values of the corresponding fields in the table. It is important that here is achieved universality, independence from the table for all options for entering words.
The solution is also easy when a list structure is used instead of a table array. Essentially, nothing but data access, which can be strictly localized in the relevant procedures, will not change. Run this solution yourself. At the same time, the decision to develop a textual representation of a table with numeric markup would be rash in all respects. It is more complicated and does not give any advantages even in cases when the process of building an automaton is separated from its use in time. For the same reasons, the XML option has no advantage. Another thing, if we are talking about operating with a list of words (and not with a table!). It is advisable to edit this list by running the graph building program using the appropriate word list handler and then calling the interpreter to work with the file. The rationality of this approach needs to be assessed at the stage of analyzing the life cycle of a software system being constructed.
For both satisfactory solutions, it is necessary to develop an algorithm for constructing an automaton for a given set of words. If an array table is used, then the result of such a construction should be a filled array. When the list organization of the table you need to make the appropriate list. To solve the problem, various automata can be constructed, but the effectiveness of their further use will be different. Consequently, it is possible to pose an optimization problem: the choice of such an automaton from a variety of automata that can cope with counting entries in the shortest possible time.
The construction of a graph of an automaton sufficient for solving the problem, but not necessarily optimal, can be implemented using the following recurrent description of the algorithm.
If the set of words is empty, then the graph is given by the structure:
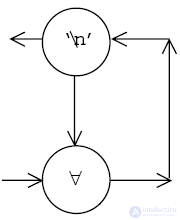
A vertex containing \ n is declared output for the graph as a whole (there is a horizontal arc outgoing from it, which leads nowhere). It is denoted further E. At this stage, the input vertex is the one that skips all the characters (by definition, it does not have a vertical outgoing arc).
Let graph G define an automaton that recognizes a certain set of words.  and let there be a word
and let there be a word  to add to this set. Adding a word is accomplished using the following steps:
to add to this set. Adding a word is accomplished using the following steps:
by word  build a list of
build a list of
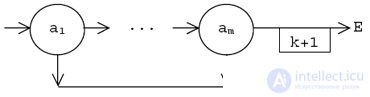
which is considered as a blank to replenish the graph G
 if there is a proper part of a word, then merging a blank with a graph is reduced to adding the mark k + 1 for the corresponding horizontal arc; otherwise skip to the following points;
if there is a proper part of a word, then merging a blank with a graph is reduced to adding the mark k + 1 for the corresponding horizontal arc; otherwise skip to the following points;for each word  of
of  looking for such
looking for such 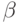 and
and 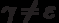 ,
, 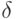 and
and 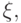 what
what  ,
,  and
and  . In column G there are fragments responsible for recognition.
. In column G there are fragments responsible for recognition. 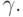 Therefore, it is necessary to glue the blank with each of such fragments, i.e., insert a vertical arc from the last vertical successor of the vertex xx 1 , ..., i to the remainder of the blank:
Therefore, it is necessary to glue the blank with each of such fragments, i.e., insert a vertical arc from the last vertical successor of the vertex xx 1 , ..., i to the remainder of the blank:
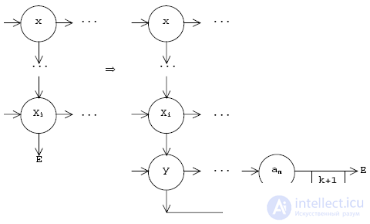
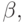
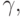
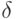 and
and 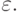
The improvement of this algorithm is possible, in particular, due to the standard method of optimizing tasks processing complexly structured interconnected information. This technique is to streamline the data. Words can be arranged in such a way that the number of checks in each (vertical) state of the machine will be minimized. Another idea of improving the algorithm is that in some cases, when linear recognition plots are relatively independent, calculate local optimal sequences and recognize their occurrences immediately. This aggregation of data is also a standard trick. Finally, multiplying the output vertex of the graph will slightly increase the efficiency. Such modifications of the algorithm are proposed to be performed independently.
* * *
The just solved problem is, of course, a model one. In practice, such problems have to be solved mainly in particular cases (for example, word intersections are ignored, instead of counting the number of entries, other processing may be required). Additional conditions significantly influence the choice of approach, but the application of the dynamically generated automaton method is a good solution in terms of efficiency, visibility and autonomy.
Logically similar problems arise in the case of preliminary planning of actions on a complex data structure, and they, as a rule, are even more difficult, although often the approach to solving them is simplified by the need to find acceptable, rather than optimal, plans. Here this method of dynamic generation and subsequent interpretation is even more valuable.
Analysis of the proposed two-stage scheme (construction of the automaton and its application) shows that the natural method of implementing the first stage is an algorithm that, at the conceptual level, should be attributed either to the style of programming, or to the recursive structural variant. As a language for its implementation, LISP, Refal and Prolog are approximately equally adequate. At the same time, an adequate style of implementing the second stage is automatic programming. Thus, the separation of styles ideally requires the use of a bilingual programming system. Unfortunately, the purely technical difficulties of interfacing two languages (we mention only one of them: the harmonization of data representations) often lead to the fact that developers prefer style modeling. And this is sometimes a pragmatically sound decision, especially if the system does not have to be developed further. But if this is required, it is better to overcome technical difficulties once, but in the future it will work conceptually thoughtfully. A good example here is the Autocad system, the language for converting plans in which is an extension of the LISP language.
It is useful to compare how our problem would be solved using styles other than automaton programming. When comparing the variants proposed above for counting word lengths, it is shown that the structured programming style is poorly suited for this task: at a minimum, it leads to redundant computations.
If we turn to sentence programming, then to solve this style, we need to abandon the agreement on stream processing, replacing it with the description of the structure of the processed data, and formulate the task in terms of this structure, as we did in program 10.2.1. Such a style is appropriate for tasks that work with more complex data structures, and only in the case when the emerging data structures are naturally processed by large-scale recognition operations characteristic of this style, and the actions are naturally presented as replacements.
The functional style is very far from the original formulation of the problem. This style does not fit well with the concepts of state, transition and action. Therefore, when developing functional and functional programming systems, special care is needed not only about supporting the style, but also about how the connection to the program of modules written in different styles will be achieved. However, the same can be said in general about any programming systems.
The jump table method is combined with an object-oriented style. It can be said that a system of objects dynamically modified by a program of this style is one of the possible implementations of a finite automaton with a potentially unlimited number of states represented by objects. With this view of the object system, the analogue of state transitions is the messages transmitted between objects. The difference between the object environment and the finite state machine only is that objects can arise (and be destroyed) dynamically, and the number of rows in the table is equal to the total number of transitions for all states and is fixed before calculations. But this difference gives a qualitative increase in the power of the object-oriented approach, indicating when it is advisable to present state tables with objects.
Of course, the above interpretation of objects is not always adequate. Moreover, in tasks that are unnaturally solved by this method, it turns out to be harmful, contrary to, for example, looking at objects as active units of a program. And this circumstance marks the boundaries of the compatibility of the object-oriented style and the method of transition tables.
In relation to a specific problem of word lengths, the object-oriented task of an automaton is possible, but it does not give anything for solving the question of automating the translation of a table view into a program. In the circuit with the handler function, duality of programs and data still complicates the construction and interpretation.
What is terrible for the representation of "live" transition tables by objects is that, although the number of objects and their relationships can change dynamically, new actions cannot be inserted into them, since the entire final set of acceptable actions is determined statically when describing object types in a program.
The style of event programming discussed in the next lecture is also often suitable for the implementation of a finite state machine. So if the task is described by the transition table, this does not always mean that it is the automaton style that is preferable. The specificity of the algorithmization of the problem can make it more convenient for programming in a different style. In a word, do not look for absolute solutions in serious works, and do not consider serious works, where they are offered to you.
In C ++ / C #, a structure that represents a graph similar to the one just described can be represented as follows:
struct union {char Symb;
struct {
bool Tag; // sign field of the current
// values in union:
union {
char Symb; // <- Tag = true
int num; // <- Tag = false
}; // union name here
// not necessary
int yes; // jump index by coincidence
int no; // mismatch transition index
} Table [];
The peculiarity of this interpretation of the table is that it corresponds to Moore’s automata: actions are associated with vertices, and not with arcs, with states, and not with transitions. The vertex that matches the action does not require reading the next character and analyzing it. Instead of symbolic annotations, vertex-actions contain numeric numbers identifying the corresponding counters (a marked union is used to reflect this convention).
Comments
To leave a comment
Programming Styles and Techniques
Terms: Programming Styles and Techniques