Lecture
Parallel programming for about 40 years is a promising direction. This is always a new topic in programming. Such a prolonged infancy suggests that all is not well with this child. Therefore, here we first of all critically analyze the basic concepts that need to be mastered, and only then sit down to encode a parallel program.
When considering the programming styles, it turned out that often the linear order of execution of program operators is imposed on it from the outside and serves only as a support necessary for implementation in a particular system.
Let us turn to the classical examples, when the computational algorithm is well parallelized.
Example 15.1.1 . Matrix multiplication is a case in which sufficiently broad masses of programmers and customers of computational programs have realized the potential advantage of parallelization. If we divide the matrix of the product k * mxl * n into submatrices of size mxn, then to calculate each such submatrix it is sufficient to have m rows of the first factor and n columns of the second. By separating the computations by independent processors, we can at the cost of some duplication of the original data get the result much faster.
Similarly, the problem of solving a system of linear equations is parallelized.
Example 15.1.2 . Let the task be represented as a set of several interacting automata (thus, in principle, it fits into the framework of automaton programming, but a single system is structured into subsystems, and most of the actions work within subsystems). Then we have a natural parallelism.
These are many of the game tasks in which several characters are involved, and most parsing tasks are the same.
Already in these two examples it is clear that there are fundamentally different cases. In the first example, the tasks are indifferent to how the result will be calculated. In such a case, we use for parallelizing the properties of a specific computational algorithm, which has many potentially computational structures that are potentially suitable for implementing information interconnections in the corresponding data network (sequential necessarily among them).
In the second example, parallelism is naturally dictated by the task itself, since the system is divided into subsystems. I hope you are not surprised by the fact that in this case, the natural from a theoretical point of view, the solution is almost almost never feasible. The current parallel systems have a fixed (usually small) number of processors, and if there are many processors, they are tied into a rigid structure. Therefore, tasks with natural parallelism are very rarely placed in the Procrustean bed of such a system. It is much easier to push there something that is not parallel in nature, but can be parallelized, since in this case the structure of the implementation of the algorithm can be tailored to the requirements of a particular system.
Thus, the main problem with concurrency is that the programming and architecture of machines come into a conceptual contradiction .
In life, each of you met with the simplest type of parallelism: a long and relatively autonomous printing process starts, as a rule, in parallel with the execution of other programs. The case when you simultaneously run several programs, as a rule, is not a real parallelism (this is discussed below).
The result of the team is the result of the participant who came last.
(from the rules of competitions in military-applied sports)
- Doctor, what am I sick with?
- Do not worry, sick, an autopsy will show.
(Russian joke)
The type of parallelism that arises when matrixes are multiplied is natural for structured programming, but in fact is not parallelism. In structured programming, data is organized into a network over which a program moves. This network is partially in order, and if there are several subnets in the network that are weakly connected to each other and pass through a certain segment of the source network from beginning to end, then these subnets can be executed on independent calculators that interact with each other at critical times. Usually such a data network partitioning is not unique, and therefore it is possible to execute one and the same algorithm on parallel systems of different architecture.
Example 15.2.1 . Let the data network have the following form (Fig. 15.1)
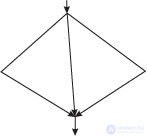
Then it is natural to execute it on a one-, two- or three-processor machine. In the case of a multiprocessor machine at the beginning and at the final stage, the calculation goes sequentially, and the three branches are distributed between the processors. In particular, if two side branches take less time to count than the main branch, it is possible to distribute both on the same processor on a two-processor machine.
In the parallelized program, the final stage of execution begins only after all three branches, which provide the initial data for it, are completed. Such parallelism, when all parallel branches need to be successfully completed to complete a block of parallel processes, typically arises in computational problems and is called the &-parallelism. How successful is the result of parallelization depends on the uniform distribution of the computational load between the branches (see the first epigraph).
Another type of concurrency was first realized on search tasks. For example, if we know that a lion who escaped from a zoo is in one of four quarters and cannot move from one to another, to speed up the search, we can (if we have enough search teams) send a team to each of the quarters, and finish the search as soon as one of the teams finds a fugitive. Thus arises 
- parallelism, when it is enough to successfully complete a parallel block so that one of the running processes comes to success.
Consider now what are the general conditions of applicability - parallelism. A private example of the lion shows that, in principle , it would be possible to present a "procedure" for finding a fugitive in the form of the following conditional sentence:
if
Lion quarter 1 -> Search quarter 1,
Lion quarter 2 -> Search quarter 2,
Lion quarter 3 -> Search quarter 3,
Lion quarter 4 -> Search quarter 4
fi
But the trouble is that to find out the truth of the guard, you need to execute a protected command, i.e. find the lion. Thus, this conditional operator can only serve as a ghost.
Further, there is another implicit condition, which is illustrated by the second epigraph. If the execution of a guarded team with improper guards can harm (the resources will take, the harm is something more substantial, like treatment according to an incorrect diagnosis), then we will most likely be forced to open the program after the sudden and painful death of the program.
In this way, - parallelism is a support for the effective implementation of a phantom conditional operator that satisfies two requirements:
Then you can run various options in parallel on different processors and see which one will come to luck.
As an example of a problem, naturally admitting> - parallelism and non-search task, we can consider the situation often arising in differential games (in particular, in the game "interceptor and carrier") when there is a point of choice. After this point, several incompatible methods are proposed, and in order to determine which of the strategies will lead to the capture of the target, it is necessary to calculate the behavior of the system with the considered strategy to the end. Then, if there is a choice point ahead and you need to make a decision in advance, it is advisable to start several modeling processes at once.
The third type of parallelism is actually not parallelism, and is perhaps the most common in programming practice. This is quasi-parallelism. You encounter it in programs when you spawn a subprocess with a command like thread. In this case, several processes are executed as one process in which the steps of the subprocesses are mixed, so that the programmer has the impression that the processes are executed in parallel. Quasi-parallelism can look from the outside like any of the two types of parallelism discussed earlier. In the first approximation, quasi-parallelism gives only a net loss, but in fact it allows you to take waiting intervals (for example, data input or output) that are naturally occurring in one of the processes by the operation of other processes. This is how your player works, while you are puzzled over errors in your program.
Since here all management is actually concentrated in one place, the methods of working with quasi-parallel processes are most developed.
And, finally, the last case of parallelism, when processes are not just run parallel with each other, they run on different, often poorly related, calculators. For example, the server is running a search in the database, and the main program is running for you. This is a distributed execution . Recently, such a case has also been well developed, because in such a difficult situation, any shortcomings can lead to the agony of the program.
Example 15.2.2 . A classic example of effective use - parallelism on a poorly interconnected distributed system is a massive hacker attack of a password. Thousands of hackers, dividing the search field between themselves, launch brute force programs on their machines. Someone will find it, and the fact that others can spend a few more days (since at night hackers usually “work” and sleep during the day) to drive the brute force program doesn’t affect anything: anyway, the gain is enormous.
So far, we have considered the ideal case when processes are independent among themselves and the question of their interaction arises only at the moment of their completion. But in practice, of course, this is extremely rare. Processes are almost always interconnected, and therefore it is necessary to consider the issue of organizing connections between them.
The first connection is general data. Consider the simplest case when processes have a common memory field in which they write updated data and read them if necessary. Even in this case, there are difficulties. If one of the processes began to update the data in the field, and the other just at that time reads them, then it may happen that he gets a jumble of old and updated data (such a case in distributed systems and in databases is considered as a violation of data integrity 1 ).
Here we should introduce the concept of a critical interval , when a program occupying a certain resource must be sure that no one else can turn to this resource, that its “friends” working in parallel cannot harm or be disoriented.
Of course, the easiest way to establish exclusive use of a shared resource: the program that accesses this resource sets the flag, and while the flag is raised, no one else can access it. But imagine, for example, the collective work on a puffy technical task. I need to, say, make changes to Chapter 3, but I cannot do this, because for a couple of hours someone has been working on Chapter 13, which practically does not depend on Chapter 3. In this case, corporate support systems for distributed work are resorted to (Lotus Works can be cited as a positive example of a stable system, although the author has not worked with it since 2002, so improvements since then could have led to a loss of reliability). They solve subtle problems of maintaining data integrity when changes are received from multiple sources, when server, network, etc. fails. All this is done in such a way that the work of one of the employees practically does not interfere with the work of the others (and if it does, then both are trying to get into the same place, but for these cases a system of conflict resolution is provided).
The critical interval, as often happens in programming, is a concept that exists in two ways: hardware and logic. The logical critical interval is determined (or rather, in principle should be determined) by the needs of the program system and can be set by natural software. But the trouble is that for equipment even such an elementary action as checking the employment flag of a resource and setting its new value can be divisible, and in the interval between your reading and writing, someone else will write down that the resource is busy and then. .. Therefore, there are hardware critical intervals that are hidden for a regular user within synchronization commands. The system tries to minimize these intervals, since at such times when the critical process is stopped and transferring control to another is extremely undesirable. Another thing is the logical critical interval. Here you can pause the process and start another one, as long as it does not access the closed resource.
When a shared resource is one, everything is more or less clear. But when there are a lot of them, several of them may be required at once ...
Example 15.3.1 . Five European philosophers walk deeply around the hall, not paying attention to each other. In the middle of the hall is a round table with a spaghetti dish, five chairs and five forks, one between every two chairs. When the philosopher feels that he is hungry, he sits down on a random free space, picks up the plugs on both sides of it (if necessary, waits until they are free), sat up and gets up to continue thinking. As European philosophers, they will not eat spaghetti with one fork, and since they are self-absorbed philosophers, they completely ignore the fact that forks are not washed 2 .
If all five philosophers sit at the table at the same time and take a fork in their right hand, then they will die of hunger at that table.
This example is the classic parallel programming problem. All theoretical disciplines of parallel process control are tested on it.
The second type of connection between parallel processes is critical points . When a process has reached a critical point, this means that it can move on only if other processes also reach the corresponding critical point. For example, to calculate the next iteration, you need to make sure that the previous iteration is already over by everyone. For the next search, you need to know that at least one of the processes running in parallel has already found the previous data.
There is one important special case of the & -parallelism, when critical points and critical intervals do not cause problems. This is pipelining . With pipelining, most of the time, the processes run independently. Then the work of all private processes is suspended, the data is exchanged and events are viewed. Such an organization of work is similar to the factory conveyor: while the conveyor is standing, workers perform their operations; then the conveyor moves, passing the results of the operations to the next performer.
It was an informal introduction to theoretical subtleties arising from the interaction of processes (anyway, really parallel or quasi-parallel). But in practice, other details are often more important.
Good parallelization is impossible without a detailed analysis of the program. In fact, if one of the processors carries 99% of the computational load, then we only lose on parallelization, as the overhead of process synchronization will be added. So the first problem of practical parallelization is the prediction of the complexity of computations of various program blocks. Only if it is possible to evenly distribute the computations among the processors, and this uniformity should be maintained within each interval between the interactions of the processes, does the parallelization give a gain. In parallel programming, the author observed examples when, seemingly innocuous and absolutely correct from the point of view of ordinary programming, the enhancement of one of the blocks led to a deterioration in the work of the entire program. So optimization is not always monotonous with respect to partitioning into subsystems.
Now let's look at one of the quasi-parallel programming methods, often well suited for modeling the natural parallelism of automata programming and the potential parallelism of event programming. This is a simulation in a logical discrete time system.
The concept of time is one of the most important in many fields. Moreover, in the famous American aphorism Time is money, absolute value is reduced to the level of conditional value. We cannot get time from anyone, we cannot save it, we can only waste it.
When computer modeling the behavior of objects, it is advisable to highlight two aspects:
If time is not modeled, but taken from the real world, they talk about real-time systems. If time is part of the virtual world of the system, then this is a logical time. Highlighting its applied aspects, they often speak of logical time as conditional , or model, time.
Let us consider the simplest (but extremely important) case of time, when time can be represented as a linearly ordered set of steps, and all processes occurring between steps can be considered indivisible. Then on the time axis we have only a discrete set of points at which we need to maintain the integrity of the system and each of the processes. Such discipline is also possible for real-time systems if some delay in response to an event is acceptable (this case is called soft real time). Then we can wait for the natural completion of a step in our process and only view events in the interval between steps.
If time is not only discrete, but also logical, then we are talking about a system with discrete events . This situation is well suited for both modeling and pipelining and - parallelism.
Example 15.3.2 . Consider a model problem. Suppose you need to find the shortest path in a loaded directed graph, where each arc is equipped with a number interpreted as its length. It is traditionally interpreted as defining the shortest path between cities A and B, connected by a network of unidirectional roads.
Let us show that the solution to the problem can be constructed as a system of interacting processes with discrete time. This is a good method of structuring a problem and separating the details from the essential features: first we build an abstract representation, and then we make it concrete, for example by placing an essentially parallel algorithm within the framework of a sequential program. The idea of this approach goes back to W.-I. Dalu and C. Hooru, who used this problem to demonstrate the capabilities of a discrete event system provided by the SIMULA 60 and SIMULA 67 languages, which coincided in the time model and process control structure.
The basic concept in this problem is naturally 15: Problems encountered in parallel programming - portal intellect.icu - parallelism. Determining the shortest distance can be represented as a competition between active agents “scattering” along different roads. Two classes of algorithms are immediately distinguished: direct, when the overall process begins with A, and reverse, for which B is assigned as the starting city. To show the fundamental points, it is enough to consider one direct and reverse algorithm each.
A direct algorithm for scattering agents can be described as the behavior of each agent according to the following scheme, the parameter of which is the location of the agent:
It can be seen that the algorithm terminates when a path from A to B is found or when all agents are eliminated.
As usual, more stringent conditions for the final program entail in many respects softer requirements for the prototype (it is necessary to expand the possibilities of its restructuring into different versions of the final program), but at the same time it is desirable to increase the level of concepts of the prototype as much as possible. If the program ends up being implemented quasi-parallel, there is no need to pay attention to how many agents can act simultaneously. In particular, in the case of a known path from A to B, one can not check the prohibition or weaken it until the case when the ancestor of a given agent visited a given city, and, therefore, he ended up on the remembered path. In this case, there is no need to remember global, or more precisely, information common to all agents about the graph of roads and cities.
The above algorithm requires storing information about the path traveled in the local data of the agents. Thus, the local data of each of the agents that will be eliminated is stored in vain. If you forget them, then the desired path cannot be obtained; only some of its characteristics are obtained. The solution using inverse walk is free from this drawback, i.e. from B to A. For him everything works exactly the same except for the following:
local information about agents and their paths is not remembered;
as a note about the visit, it is indicated from which city the agent came to this city (this can be called a recommendation mark).
As a result, when any of the agents reaches A, the sequence starting with A and building up according to the recommendation marks gives the desired path.
Fig. Figure 15.2 illustrates the operation of all three algorithms: direct (a), forward with marks (b) and reverse with marks-recommendations (c). The inscriptions on the arc-roads denote agents, and the superscripts on them indicate the order in which agents are generated. Locally stored information about the visited cities is written in oblique brackets. Crossed-out inscriptions indicate the destruction of the agent in connection with the use of information about visits to cities.
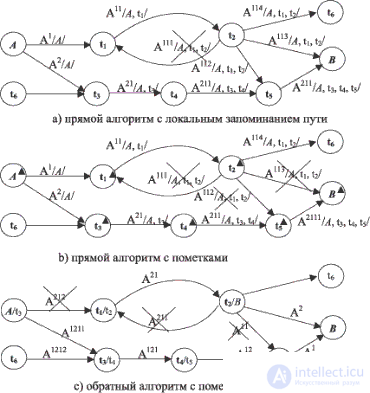
Both direct and reverse algorithms are workable if you ensure that all agent processes operate simultaneously. If the computer allows multiprocessing, with a potentially unlimited number of processors, then this condition is met automatically.
If parallelism is possible, but there are not enough processes (for example, if you decide to use the Prolog system Muse to implement these algorithms), then we are in a difficult situation that requires creative solutions, a combination of scientific and engineering approaches.
The question arises about means of emulating discrete events. There are packages for working with discrete events, but back in the 60s. it has been shown that thinking in terms of time actually requires a language of its own. The classic example here is still the SIMULA 67 language. It explicitly proclaims the simulation of parallelism and therefore allows humans to think in terms of acting agents, which seems to be a more flexible and natural way of expressing many algorithms. The discrete event system can be considered as a general method for overcoming the contradiction between fundamental parallelism and the actual sequence of calculations.
The classic implementation of discrete event systems is a general process support environment. Each process can be in one of four states, which are determined using the so-called control list: a strictly ordered queue of processes assigned to execution. In a good implementation of the classical model, this list is hidden.
For each process, a data structure is determined that is sufficient to completely remember its state at the moment when the discrete step is completed 7. The remembered state is called the resume point.
The design of the control list simulates time. The first process is always active. This is the only active process. If he interrupts his execution, the suspended process following him becomes active. A process can be inserted into the control list ( before any process in the list or after it, after a certain time) or deleted from it. A process can also be assigned for a specific time , it is inserted before the process, the execution time of which is minimally higher than the one being scheduled. Perhaps a random (pseudo-random) action to insert a process into one or another place in the control list.
We can assume that with the help of the control list processes are set relative priorities.
It is postulated that all operations with the control list and with the activity states of the processes are the result of discrete events in the system. Until any of the events has occurred, the state of the process and its position in the control list cannot be changed.
It can be seen that this is a simulation model that creates a structure that is practically indistinguishable for an external observer from real parallelism, and with an unlimited number of processors. Since we have a system with discrete events, logical time and time delays are only a means of restructuring the control list.
As follows from the above, in relation to the problem being solved, copying agents means:
According to the event postulate, the execution of any agent process cannot lead to a change in the planned order of execution of other processes until an event occurs. In this case, the events are the expiration of the time delay, as well as the self-destruction of the active agent, as a result of which the next control list process becomes active.
For example, for the inverse algorithm with notes-recommendations, the diagram of the program of the agent who came to the city is as follows:
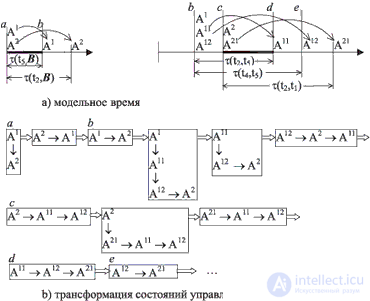
In fig. 15.3 depicts the beginning of the sequence of states of the control list, which is obtained by executing the algorithm with the data shown in Fig. 15.2s. At the top of the figure, the time model is depicted: on the horizontal axis, there are moments when the state of the agents changes (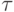 
- function of travel time between cities; a, b, c and d - moments for further explanation). In the lower part of the figure, the sequence of changes in the control list is shown (its states are indicated by rectangular blocks, in which, for clarity, vertical arrows indicate connections of processes assigned to the same time, and horizontal arrows indicate the ordering of processes by model time).
The deflation of agents begins with the spawning of processes A1 and A2, which corresponds to two roads leading to city B. This is the moment of model time, marked as a. The moment b corresponds to four states replacing each other, c corresponds to three, and ad represents one state. Comparison of Figures 15.2a and 15.2b shows that no special modeling of time, and even more delays is required: time changes "instantly" when all events assigned to earlier periods have worked and an event assigned to later term. In principle, even the time attribute is not required here - the order relationship between events is sufficient .
Even looping some agents will not interfere with the execution of the algorithm, if only the capacity of the control list is sufficient.
It is necessary to emphasize a number of important points:
We can be recommended as a good presentation of the current state of affairs in the technique of practical parallel programming. In particular, the MPI system described in this book, and now the very widely and unreasonably advertised Open MP system, includes means for the quasi-parallel execution of parallel programs that are different from the system with discrete events. We do not describe these tools, because for real programs they are needed only as a method of debugging parallel programs on a machine with insufficient configuration (and a method that does not cause much enthusiasm).
Comments
To leave a comment
Programming Styles and Techniques
Terms: Programming Styles and Techniques