Lecture
From the materials of the previous section, it is clear that approaches to solving programmer tasks using different languages differ from each other. Sometimes these differences are not fundamental and come down only to the textual representation of the program, and sometimes they are quite substantial. If the differences are not fundamental, then we say that languages have a similar model of computation.
The computation model of a language does not necessarily coincide with the computation model embedded in the equipment. These models diverge if the machine itself has a traditional architecture. Moreover, even machines of a different architecture are programmatically modeled on machines of traditional architecture. In the following, we will use the term traditional languages, meaning by this languages, the computation model of which is inherited from the traditional architecture of machines. The architecture first used by Konrad von Zuse 1 was still at the turn of the 1930s – 40s. XX century., In a slightly modified form is still adopted for almost all computers.
This computing system architecture has the following three elements:
These elements have the following features.
The value in the cell, from the point of view of the processor, is a sequence of bits of a fixed length without any restrictions.
From the homogeneity of the memory it follows that the commands and data (processed values) are located in a single shared memory and are equally addressed.
Such architecture will be called traditional .
The traditional machine architecture is specified for the respective application environment. In particular, it is always complemented by input and output devices.
In fig. 2.1 shows the interaction of devices of a traditional machine.
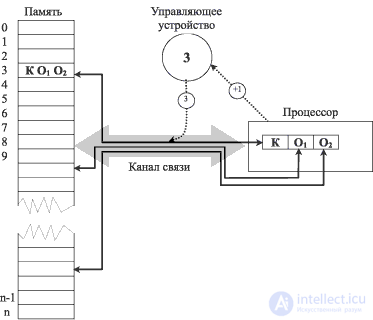
In the team KO 1 O 2 K is the operation code, O 1 and O 2 are the addresses of the operands. The team is located at address 3. The solid arrows indicate the transmission of information through the channel. The dashed arrows indicate actions that are carried out immediately before the command is executed (a request for the command code at address 3) and after it (an indication of the need to request a command following in the memory of the executable).
Traditional computer architecture was formed in the conditions of unreliability of physical elements. In particular, for this reason, a rather primitive method of control was chosen: transfer to the next command or to the command at the forcibly assigned address. And in the future, despite the emergence of a qualitatively new elemental base, the rapid growth in the production of machines of this type prevented a change in architecture.
There is a reason due to which the increase in the efficiency of traditional machines is fundamentally limited. Increasing the speed of the processor as an active piece of equipment leads to an increase in the counting rate only within the limits determined by the speed of the communication channel between the processor and memory: if it is low, the processor will be idle waiting for the next instruction, operands, or completion of assignment 3 . The growth rate of the processor speed is higher than that of the communication channel.
These fundamentally insurmountable limitations of the classical computational model were pointed out by Backus in the mid-seventies (Backus's Turing lecture [35]), calling the memory communication channel with the processor a bottleneck (literally bottleneck ) of the traditional model.
The traditional architecture of machines is least related to a specific class of tasks. Rather, it is associated with the two most common and most low-level programming styles: structural and automatic programming.
By programming style, we mean an internally conceptually consistent set of tools based on some logic of program construction. Theoretical studies of the last decades have shown that different logics of building programs correspond to different classes of tasks and methods, and these logics are incompatible with each other. Logic (and, accordingly, programming styles) provide the most common shell, independent of specific subject areas and even of specific methods. As soon as we understand the peculiarities of the methods, the styles begin to concretize further. So, known to you (since it is he who is taught as the only one existing in all modern textbooks on the beginnings of programming), the structural style is specified in a cyclical or recursive version (hypostasis).
For different styles, the logic of construction is incompatible, so before discussing styles in the system, we will get acquainted with examples of the implementation of different styles. But even before that, it is advisable to consider other machine architectures.
After it became clear that the traditional architecture impedes the performance gain, it began to change. Below are the most common modifications:
The usefulness of such modifications is obvious. But caching, other changes of the classical canonical model, and even processors, are only half measures that allow to expand, but not to eliminate, the bottleneck.
Attention !
An important consequence of the traditional structure of a computer is the following: in a machine program, all actions and conditions are local .
To improve the efficiency of the equipment, sometimes the principle of memory uniformity is discarded. We mention two architectural modifications of the traditional machine.
Some (primarily specialized) machines provide for explicit allocation in the memory of data areas and command areas. In the normal mode of program execution, the processor is not allowed to write anything into the command area, as a result, the reliability of the programs increases. To record something in the command area, you need to enable the corresponding mode 4 by hardware.
But the separation between the teams and the data is rather coarse. It is useful to consider the architecture in which the so-called tagging is proposed. Its meaning lies in the fact that special digits are allocated in the cells (main memory), called the tag , which indicate the type of value stored in the rest of the value (see Fig. 2.2).

Hardware tagging provides the following benefits.
In linguistic terms, tagging is expressed as dynamic (determined when the program is executed) data typing. In this regard, tagging in hardware was about ten years ahead of the first experimental attempts at dynamic typing in programming languages. Now dynamic typing, from a logical point of view completely analogous to tagging, is one of the tools of object-oriented programming.
In C, tagged data corresponds to a description of a structure similar to this:
struct tagged
{
int type_tag;
union
{
int x;
float y;
}
} In Pascal, a tagged cell can be represented by the following variant structure:
record case tag: Boolean of true: (i: integer); false: (r: real) end;
Tagging is great with structured programming, and therefore is almost always used in conjunction with a modification of the addressing and memory structure called stack architecture. When implementing high-level languages in modern programming systems, a context structure is almost always created.
In the stack architecture of the machine, the physical memory is already organized as a structured stack of contexts (see Fig. 2.3).
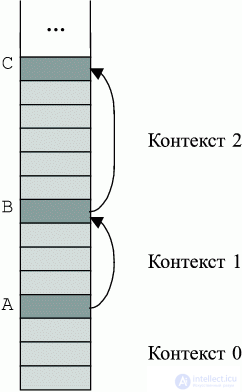
The stack grows down. The current context is called Context 0. The lowest unit on the stack is the current result. The stack is structured as texttex. Each substlet includes data for a program block. Thus, each of the sub-codsets sets the context for the calculations in the corresponding block. At the beginning of each substep there is its marker , which contains all the necessary official information about the substeck, in particular, a link to the previous marker.
For an abstract calculator with a stack, at the beginning of processing each construction, you need to memorize in the stack the current instance of the context state. Then you can perform the usual steps to calculate the structure.
The stack architecture was embodied in the command systems of the machines of the Barroughs and Elbrus series. They perfectly proved themselves to be machines for complex demanding computations, but they could not stand the competition with the PC armada, which were crushed by their number and cheapness.
There is an opposite direction for the development of equipment. In machines with the so-called RISC architecture, machine commands are extremely simple, but in the semi-permanent part of RAM there are subroutines for commands of the “normal” or even “high” level, so that, in principle, the RISC processor can emulate 5 machines of different architecture depending on the mode . For example, such a system was used in the machines of the famous Power PC series - Power Mac, which could perform for both the user and the programmer both as a PC and as a Macintosh. This series suffered a commercial failure rather because of mistakes in promotion to the market than because of the lack of real merits.
Cool thought. He liked this. He decided to think again at his leisure. Russian anecdote
Historical excursion
During the Great French Revolution, in connection with the introduction of the metric system of measures, and to improve the quality of artillery and fleet, it became necessary to quickly and qualitatively recount many tables: artillery, navigation, astronomical, geodesic, etc.
The solution of this problem (the mastermind and organizer of the work was an eminent mathematician and administrator L. Carnot) was brilliant from the point of view of conceptual and organizational elaboration. First, using interpolation methods, all functions were replaced by their piecewise-polynomial approximations that have no discontinuities (the modern term is spline). Polynomials can be calculated by the finite difference method; therefore, the algorithm for calculating a polynomial was distributed over additions, subtractions and a small number of multiplications of the constants. To organize such calculations, two companies of parallel working literate soldiers under the guidance of mathematicians were used. The same calculations were carried out by the companies independently. Each soldier received arguments from the two comrades indicated to him, added or subtracted them (the action was predetermined in advance and did not change). The most competent soldiers received an argument from one comrade and multiplied it by a given constant. At the command, the results of the actions were transmitted further. Mathematicians-wardens checked the results for plausibility and recalculated them selectively. In cases of discrepancies in the results of the mouth account was made again. Thus, the tables were recalculated with virtually no errors, with minimal cost, high accuracy and in the shortest possible time. As a result, the artillery tables of the French army remained the best for more than five years, until the Russian gunners under the leadership of c. Arakcheev did not consider them even better 6 .
So in the first historical case, when a significant amount of computation was industrialized, the computation model was very skillfully chosen.
It was this example that Charles Babbage was guided by when creating the first software-controlled mechanical computer, since it was impossible to achieve an acceptable speed on mechanical elements without parallelizing the calculations. High-speed, but unreliable elements of the first computers practically forced to abandon the parallel model of computing and move on to a more primitive sequential model. All teaching and software began to evolve with a focus on sequential computing. And when the possibility of electronic implementation of parallel computing appeared, neither mathematicians nor programmers were ready for it.
First of all, you can just have multiple processors. Multiprocessing can be used in several ways.
Прямое развитие данной идеи наталкивается также на массу тонких вопросов синхронизации. Простейший и наиболее очевидный из конфликтов синхронизации - попытка одновременной записи результатов нескольких команд в одну ячейку памяти, поэтому присваивания становятся тормозом на пути программирования.
Рассмотрим теперь те архитектуры, где до известной степени ликвидируется централизованное управление и появляется возможность глубокого распараллеливания вычислений.
Здесь стоит обратить внимание на два взаимосвязанных момента. Во-первых, часто нет нужды в хранении промежуточных результатов счета и, как следствие, потребность в пассивной памяти существенно снижается. Во-вторых, ликвидируется примитивное устройство управления, а его роль принимают на себя элементы оборудования, отвечающие за выяснение готовности команд к выполнению. Это - одна из схем, которая подчиняет управление потокам данных (data flow). Такие схемы противопоставляются управляющим потокам (control flow) традиционных вычислений.
Рассмотрим гипотетическую схему машины, управляемой потоком данных. Каждая команда имеет ссылку на те команды, от которых она зависит ( предпосылки команды). Если выполнены все предпосылки, команда имеет право выполниться. Например, рассмотрим следующую схему.
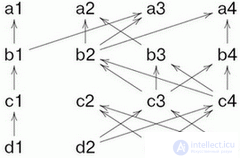
На схеме вершины означают команды. Каждая команда зависит не более чем от двух, но зависеть от нее может сколько угодно других.
Представленная идея неоднократно воплощалась в оборудовании (так называемые машины потоков данных). Но каждый раз узким местом для подобных машин оказывалось несоответствие стиля программ, требуемого для них, тем стилям, к которым привыкли программисты. Как следствие, в каждом из таких процессоров делались грубые системные ошибки, приводившие к затруднениям в программировании, а также к понижению скорости и гибкости вычислений. Тем не менее поскольку скорость света очень скоро поставит предел механическому увеличению пропускной способности каналов, к подобным схемам придется вернуться на другом уровне.
Конечно же, при реализации идеи возникают сложности. Пару из них демонстрирует следующий поток.
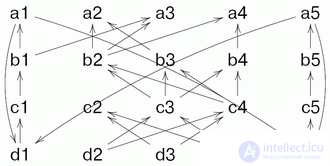
В потоке имеются два цикла, подготавливающие данные друг для друга. Возникает вопрос, а если один из циклов вторично подошел к точке, где требуются данные из другого, не устарели ли уже имеющиеся данные и не нужно ли подождать, пока они обновятся? Далее, здесь видно, что инициализацию потока данных часто необходимо выделять в самостоятельный блок, поскольку формально вычислениеобоих циклов просто не сможет начаться.
Машины потоков данных уже несколько десятилетий используются на практике, так называемые суперЭВМ считают вычислительные задачи колоссальной трудоемкости (например, метеорологические). В подобных задачах, как правило, вычисление может быть записано в матричной алгебре, и новые матрицы строка за строкой вычисляются по старым. Таким образом, можно организовать конвейер , когда элементы целого вектора данных параллельно считаются по элементам предшествующего вектора, а переход к следующему происходит, когда все новые элементы посчитаны (так что вопрос о старении данных решается радикально: все, что использовалось для предыдущего вектора, по умолчанию считается устаревшим для следующего). Особенно хорошо конвейер работает, когда подпрограммы вычисления для каждого из элементов массива практически не изменяются (конечно же, для разных элементов они могут быть разные), посколькуинициализация процесса занимает много времени и сил. Конвейер с 1024 процессорами увеличивает производительность вычислений для некоторых реальных задач примерно в 300 раз, и для многих приблизительно в 100 раз. Первой серийной суперЭВМ, успешно применившейконвейерную организацию, стала система машин Cray.
Одной из особенностей машин потоков данных является повышение активности памяти, в которой размещаются команды и их операнды. Поэтому пути можно пойти еще дальше, сделав всю память активной. Во избежание полной анархии, память обычно имеет общее устройство управления, задающее одну команду (или несколько команд, в зависимости от какого-то быстро проверяемого условия), которую выполняют все ячейки ( ассоциативная память ). История реализации этой идеи аналогична истории машин потоков данных: аппаратные предпосылки есть, но эффективных способов программирования нет.
Несмотря на очевидные преимущества для отдельных классов задач других моделей вычислений и на очевидную неэффективность классической модели вычислений, не происходит переход к другим, более перспективным с точки зрения ускорения счета, моделям. Why? Это очень непростой вопрос, связанный как со сложившимися традициями, так и с огромным грузом накопленного программного обеспечения. В частности, другие модели вычислений, очевидно, не универсальны, ориентированы на некоторые классы задач, а иллюзия универсальности, основанная на примитивно истолкованной теореме об универсальном алгоритме, сопутствует традиционной модели вычислений. Но, пожалуй, более всего консерватизм обусловлен тем, что сегодняшняя армия программистов воспитана на традиционной модели, и она уже не в состоянии перестроиться.
Уже в машине потоков данных мы видим, что приказ выполнить следующую команду может быть заменен на разрешение ее выполнить. Таким образом, в программировании имеется возможность перехода от повелительного наклонения к изъявительному. Реализация идеи внедрения изъявительного наклонения в языки программирования возможна по следующим направлениям:
The method of transferring data and activating calculations in a switching system can be considered as one of the implementations of data flow in a system of functions. In particular, if a graph has no cycles, then the switching system becomes a form of representation of a non-recursive system of functions. If the graph of the switching system contains cycles, then it can be interpreted as a recursive system of functions. Such a system can theoretically be represented as an infinite acyclic graph.
In the case of the most common classical logic and the language of the predicate calculus, or some of its extensions to the axiom system, you can look at the description of the subject area (or, equivalently, at specifying the relations between the data). Computational actions in such a system are activated by requests, the purpose of which is to derive some formula (which for classical logic and elementary formulas corresponds to the conclusion of truth or the falsity of some fact; such a conclusion can no longer be called a test, since it is not an elementary operation). A programmer in such a system is usually not interested in the method of output, but only in its feasibility.
Everything described above, if it can today be implemented in equipment, is extremely detrimental and private. But back in the 60s. It became clear in the twentieth century that software shielded the physical structure of a computer so strongly that for all users and most programmers the computer together with the basic software is a single system. In this regard, they increasingly talk about the programming system as a machine. For example, the implementation of the Java language is determined by a Java machine, in terms of which all calculations are understood. Quite often, such a software machine that implements a certain model of computing served as the basis for the hardware implementation of the key features of this model. For example, Algol-machine formed the basis of computers with stack architecture and tagging.
Comments
To leave a comment
Programming Styles and Techniques
Terms: Programming Styles and Techniques