Lecture
Logic programming language PROLOG is one of the models of penal programming. We use only those features of the PROLOG language that are consistent with the standard adopted in 1996 [36]. As a programming guide in the PROLOG language, you can use, say, the book [6]. It contains the smallest number of shortcomings and frank errors, as well as the greatest number of practical tips compared to other manuals known to the author.
The first discovery of the creators of the PROLOG language was the concept of unification, invented in the resolution method for proving the formulas of classical predicate logic.
Two expressions are called unified if they can be reduced to the same type by substituting the values of free variables. Unification — a form of instantiation, in which the boundaries of all syntactic units are fixed, the structure of the expression is uniquely defined, and the substitution that reduces the two expressions to the same type is calculated recursively.
The second finding, transferred by the authors of the PROLOG language from specialized programs (for logic and artificial intelligence) to programming languages, was the system for handling failures. Successful unification is only permission to perform some action. After checking other conditions, we may be forced to return and choose another option.
The third finding of the PROLOG language, transferred to programming from the resolution method, is the standardization of the goal. The purpose of the proof in the resolution method is always to get an empty clause, that is, to erase the expression being proved (from a logical point of view, to bring it to the point of absurdity). Similarly, in the language of the PROLOG: the successful execution of the program means erasing the field of view.
The fourth find of the creators of the language PROLOG is taken from the limitation of classical logic. Horn's formulas
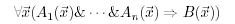
possess an important property. To find a conclusion in the system of Horn formulas, it suffices to produce the so-called linear resolution, when at each step a conclusion is drawn from the original formula and the heir to the goal. In principle, there is no need to make any combinations of the original formulas among themselves or of various options for disclosing a goal between them.
When considering the execution of a program in an unconventional language (for example, the PROLOG program), then it is natural to perceive a concrete implementation of the language as a new machine of an unconventional architecture with high-level commands (in this case, a PROLOG machine).
The data used by the PROLOG machine is located in all parts of the memory field and has a common structure.
Consider at the level of abstract syntax the structure of the data processed by the PROLOG language. All data of the PROLOG language are terms. Terms are constructed from atoms using functional symbols. Atoms can be variables and constants, in turn, dividing into names and numbers. Functional characters are names and are called functors . Among functors, there are determinatives that, in the implementation, are divided into predicates and built-in functions (functions are usually used inside expressions, and predicates are the basic units of control and are usually used outside parentheses as the main functional symbol of an expression). Determinatives must be described in the program, and the remaining functors are considered simply as structural units and may remain undescribed.
In the memory field, there is a field of view containing the data directly processed by the program. It is also called a goal and consists of a sequence of terms.
The memory field has a hidden (when using the standard language features) part in which the program execution history is traced so that, if necessary, it can process the failure.
And finally, the PROLOG program itself is placed in the memory field, which is naturally structured into two parts, often mixed in the text of the program itself, but usually shared when using external memory: a database and a knowledge base.
The database consists of facts, representing a predicate applied to terms.
The knowledge base consists of sentences (clause). Each sentence has a form similar to the Horn formula.
grandfather (X, Z): - parent (X, Y), father (Y, Z).
The proposal consists of the head expression (corresponding to the conclusion of the Horn formula) and its disclosure : several expressions connected as successively achieved subgoals (they correspond to the assumptions of the Horn formula) 1 .
At any time during program execution, the database and knowledge base can be modified.
We now turn to a specific representation of the data.
In a specific syntax, language variables are represented by names consisting of letters and starting with a capital letter or with an underscore _. The variable _ is called an anonymous variable and is considered different in all its occurrences.
The constants of the PROLOG 2 language in a particular syntax are divided into names (identifiers beginning with a small letter or a set of several special characters like <, =, $), characters and numbers (characters are identified with integers that are their codes). An arbitrary sequence of characters can be made a single constant, for example:
'C: \ "SICS Prolog" \ program.pl'.
Any constant name can be a functor. Functors are distinguished by arity (that is, the number of arguments), so there can be several functors with the same name at once. For example, write (a (1)) and write (a (1), file1) use different functors. Some functions can be described as operations (infix, prefix, or postfix). Unlike almost all other languages, operations are considered only as a reduction for expressiveness. For example, x + y means exactly the same as + (x, y).
For some of the predefined functions and predicates in the system, there are additional restrictions on the arguments 3 . For example, in the function load (f) f should be the file name.
The field of view (target), containing the data directly processed by the program, consists of a sequence of terms, separated either by commas (in this case, they are understood as "consistently achieved subgoals"), or with symbols, in this case, the subgoals are "alternative." is the case of successively achieved sub-goals, through which the semantics of alternative sub-goals is determined 4 .
In a specific presentation, a sentence, for example,
grandfather (X, Z): - parent (X, Y), father (Y, Z).
It is also considered as a term, since names, (here the comma symbol is the name of an operation) and: - are considered as infix operations, and the comma binds more strongly.
As a rule, sentences related to the same predicate are grouped together, for example:
parent (X, Y): - mother (X, Y). parent (X, Y): - father (X, Y).
The order of the proposals is significant.
The database consists of facts . Facts can be expressed in one of two ways. First, a fact can be considered as a proposal that immediately leads to success (success is erasing goals). Therefore, it can be written:
father (ivan, vasilij): - true.
Here we met with one of two standard objectives: true indicates an obvious success, and fail - an obvious failure.
Secondly, especially for the facts there is a cursive, meaning the same thing:
father (ivan, vasilij).
In principle, all other structures of the PROLOG language are expressed in terms of the elementary ones defined above. But some of the structures are pragmatically so important that they have received a separate design and a more efficient implementation. These are, above all, lists and strings. A list , in principle, is defined as a term constructed from other terms and an empty list [] using a double-spaced functor (head, tail). Standard composition
. (a,. (b, ...,. (z, [])..))
is understood as a linear list and is denoted by [a, b ,. . . , z].
To indicate the attachment of several data terms to the top of the list there is a standard operation.
[t, u | L].
Strings are treated as linear lists of character codes and are denoted by a sequence of characters taken in double quotes:
"Well, got what you were looking for? Answer y or n."
The mechanism for introducing new operations into the PROLOG language is worth mentioning. Each user can define his own unary or binary operations or override standard ones. Let us give as an example the description of some standard PROLOG language operators:
: - op (1200, xfx, ': -'). : - op (1200, fx, [': -', '? -']). : - op (1000, xfy, ','). : - op (700, xfx, [=, is, <, = <, ==]). : - op (500, yfx, [+, -]). : - op (500, fx, [+, -, not]). : - op (400, yfx, [*, /, div]).
The first argument in these descriptions is the priority of the operation. It can be from 1 to 1500. The second argument is the operation template; x denotes an expression with a priority that is strictly less than the priority of the operation; y is an expression with a priority that is less than or equal to the priority of the operation, f is the position of the operation symbol itself relative to the arguments. Thus, the yfx pattern for an operation means that XYZ is understood as (XY) -Z, the xfy pattern for a comma means that t, u, r is understood as t, (u, r), the xfx pattern for: means that it is impossible use several such operations in a row without additional brackets. Operations with lower priorities bind their arguments more strongly. The same atom can be defined both as a unary and as a binary operation.
The example of operations descriptions shows that even the local use of the distinction between concrete and abstract syntactic representations of a program makes it possible to get great advantages. PROLOG did not have to deal separately with the semantics of operations, since they are not in the abstract syntax. Many subtle questions related to, inter alia, the ability of the PROLOG program to transform itself (see Test 7), are automatically eliminated.
Julia Robinson proved (see, for example, [30]) that for first-order expressions there is an effective unification algorithm that finds a unifying substitution for the two expressions or justifies that there is no such substitution.
Example 6.3.1 . Two sequences of expressions
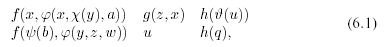
where a, b are constants, and Latin letters from the end of the alphabet are variables, are unified into
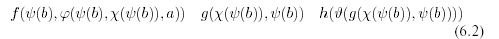
by substitution
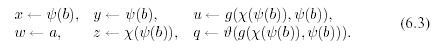
And in two sequences
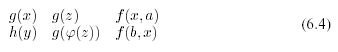
no two corresponding expressions can be unified.
Already in the above example, it is clear that unification is a global operation.
Note that the logical unification algorithm has the property of partial execution: if the two substructures are unified, then after the unifying substitution is executed, the unification of the remaining substructures can be continued, and the result of the unification will not change. So expressions can be unified one by one.
Moreover, it would be possible to unify any internal subexpressions corresponding to each other in an arbitrary order, if only the ambitious ones were unified after the subordinates. The author is not aware of any use of this natural and promising generalization of the unification algorithm.
In the first implementation of the PROLOG language, the main features of which later became the de facto standard, the creators made a mistake in understanding and, accordingly, in the implementation of the unification algorithm, which, for example, destroys the property of partial execution and can lead to unnecessary specification, it would be to find a more general concrete substitution. This error is insignificant, it does not affect the vast majority of programs, but sometimes it leads to the appearance of infinite terms, and some implementers of the PROLOG language proudly write that they can print and show even such terms on the screen.
Those who wish to catch an error as an exercise themselves, compare the unification algorithms described in the book [30] and [12].
Consider how the program is executed in the language of PROLOG. The program may have one target sentence that does not have a head part. It starts with a functor: - or? -. In a program broadcast and executed in batch mode, the first functor is usually used, and the second is used when setting the target from the terminal in dialogue mode. The difference between them is manifested only in the mode of dialogue. The second variant of the goal allows the user, after finding one of the solutions, to continue the execution of the program to find the next solution. The first does not represent such an opportunity to him, the program finds some solution and stops.
The original target is called a query . Variables included in the query have a special status. Their values in the course of sequential unions are accumulated in the hidden part of the program's memory field and, if executed successfully, are returned as a response to the request.
At each moment, the first of the terms of the goal is considered. If its determinative is not a built-in function or a built-in operator with a special definition, then a sentence is sought whose head is unified with this term. In this case, first of all, the presence of sentences is checked, the determinative of which coincides with that of the first term. If there are several such offers, then a return point is created, in which the state of the program is memorized for testing possible failures.
Offers are tested starting from the first. The resulting unifying substitution is applied to all terms in the field of view and to the tail of a successfully unified sentence. After that, the tail replaces the unified head, and execution resumes. Execution is considered successful if at some step the target disappears. An execution is considered unsuccessful if at some point there is no sentence unified with it for the first of terms.
Note that the variables of the previous unifications are identified with the variables of the following unifications only if these variables survive in sight until the corresponding unification. If a variable has already received a constant value or a value in which it does not occur, then the variables with the same name are subsequently treated as new. Thus, specific variable names have meaning only within a single sentence.
If the execution was unsuccessful, the program returns to the last of the cusps ( rollback occurs) and the next order with the same determinative is tested. If there are no such offers anymore, then there is a rollback to the next return point, and so on. If the execution is rolled back to the request and there are no more unification candidates, the program ends with a total failure.
The standard response of the program to the request is Yes, if the program has ended successfully, and No, if it has ended unsuccessfully. With success, the values of all variables of the original query are displayed.
For example, if a program and its database have the form
greater (X, Y): - greater1 (X, Y). greater (X, Y): - greater1 (Z, Y), greater (X, Z). greater1 (x, f (x)). estimation (X, Y): - greater (X, Y), known (Y). known (f (f (f (f (a))))). unknown (a). unknown (b).Example 6.3.1.
then the answer to the request
? -unknown (Y), estimation (Y, X).
will be
Y = a X = (f (f (f (f (a)))) Yes
and when trying to answer a request
? -estimation (b, x).
the program will loop.
How tricky the seemingly innocent assumptions (for example, the condition that the subgoals are achieved strictly one after the other and the options are sorted out in the same order), made in the PROLOG language, can be seen from the fact that with a logical equivalent to reformulating one of the program’s proposals
estimation (X, Y): - known (Y), greater (X, Y).
the program successfully responds to the second request
No
An even more impressive example is discussed in Exercise 5.
There is another feature of the PROLOG language, which seems to be an obvious lapse, but is in fact a reflection of the result of Kosovsky and others (unknown to the implementers and users of the PROLOG language, but the best of them felt intuitively) about the incompatibility of the PROLOG and Refal models of identification. All the work of the PROLOG system is based on the assumption that the values of the variables to be unified are uniquely recruited, and the next option can be obtained only as a result of unification with another fact or proposal. Therefore, when (as is the case with lists or lines) PROLOG meets with ambiguous identification, it will never go through its different variants . He either chooses the first one (for example, when uniting the unknowns [X | Y] with the already known ZX list is an empty list), or loops in the endless repetition of the same option (see the previous bracket, which illustrates two troubles: such a unification will return, a 'new' empty list will be selected as X).
In order to evaluate an expression, there is a predefined binary is operation. It must have a second argument, an expression composed of atoms by means of functions. After applying X is 1 + 2 instead of X it will be substituted 3. Even the expression 1 + 2 remains in the same form until it falls into the second argument is.
Attention !
The fact that a certain functor is defined as an operation does not mean that it is calculated. It is simply a change in the concrete syntactic representation. In order to be able to evaluate an expression, you need to define the functor as an internal or external function. In this case, it is not necessary to make it an operation .
The PROLOG tools considered so far do not make it possible to formulate a negation. However, the negation cannot be present in the horn formulas, its presence destroys the properties that served as the basis for the PROLOG language model. But in practice it is necessary, and therefore its substitute is introduced in the PROLOG language. This surrogate allows the programmer to control the minimum return points. If the goal is the first atom! (called the clipping predicate ), it successfully unifies and destroys the last cusp. Predicate! it is used primarily to define negation as a clear failure of subgoals.
Example 6.3.2 . Consider how using! and lists it is programmed to search the path in the maze (and even in an arbitrary directed graph).
way (x, x, [x]). way (X, Y, [Y | Z]): - connect (U, Y), nomember (Y, Z), way (X, U, Z). way (X, Y, [Y | Z]): - connect (U, Y), way (X, U, Z). nomember (Y, Z): - member (Y, Z),!, fail. numbermber (Y, Z). connect (begin, 1). connect (1, begin). connect (1,2). connect (2,3). connect (3,1). connect (3,4). connect (4, end).Listing 6.3.2. Static Maze
In response to a request
? -way (begin, end, X).
the program will issue
X = [end, 4, 3, 2, 1, begin] Yes
Instead of defining nomember you can write a sentence
way (X, Y, [Y | Z]): - connect (U, Y), not (member (Y, Z)), way (X, U, Z).
The clipping predicate can be used to turn a PROLOG program into a program with traditional controls, leaving only the unification operation from the specifics of the language. In practice and in training, there are often cases when someone cannot cope with PROLOG and debug their program because it is fixated on the imperative programming style. Having learned about!, He sighs with relief and rewrites his program in such a way that it becomes isomorphic to the program in a usual programming language. As a rule, with such a transformation, the main advantages of the PROLOG language are lost, but all its disadvantages remain.
Attention !
Some of the Russian-language textbooks on the PROLOG language are written by people who do not understand the essence of other programming styles. A visible sign of such a benefit can be the continued use of cuts.
Pragmatic agreements on the order of actions in the program have led to the fact that if we write in the form of the language PROLOG trivial tautology
A: -A.
and this statement 5 is executed, the program will loop. And for this reason, and because of an error in unifying the sentence of the PROLOG language, while preserving the external form of the logical ones, in essence, they no longer have a relation to logic.
Of course, inconsistencies were used to obtain new effects. Consider the following definition.
repeat. repeat: -repeat.
If you now insert the target repeat in the disclosure of another goal and make sure that the subsequent sub-goals in most cases end in failure, and after good luck, put!, Then these sub-goals will be repeated until good luck and their side effects will be executed in a cycle.
The above definition of repeat is not necessary to write in programs. In the PROLOG standard, the built-in predicate repeat is set, potentially infinitely many times successfully unified. The enumeration of options implemented in the PROLOG language with all its flaws quite successfully simulates non-deterministic algorithms in the program.
A non-deterministic model of calculations corresponding to PROLOG can be defined in general form as follows:
Nondeterministic achievement of the goal is called a successful calculation. Thus, if any of the continuation sequences leads to a goal, then the goal of the process is considered achieved. A non-deterministic model of computation can also be used as a means of decomposing a problem to be solved, when the programmer simply puts aside the question of how the selection of variants will be organized.
There is a theorem proving that in principle a non-deterministic finite automata can always be transformed into deterministic. The idea of transformation is the gluing of states, as shown in fig. 6.1. При этом, содержательно говоря, мы создаем линейный порядок на множестве альтернатив и выбираем альтернативы в строгом соответствии с этим порядком. Именно так с самого начала поступили в языкеPROLOG. Беды в этом нет. В то время, когда создавался язык PROLOG, идея совместности (т. е. безразличия некоторых последовательностей предложений к порядку их исполнения) и недетерминированности (т. е. ситуации, когда один и тот же оператор в одном и том же контексте может давать разные результаты) как положительного фактора была только что осознана. А те, кто делают что-либо принципиально новое, почти всегда забывают согласовать свою находку с другими принципиальными достижениями того же времени, предпочитая локализовать новизну и в остальных пунктах работать как можно более традиционно. Беды начались, когда особенности конкретного упорядочивания стали беспощадно использоваться в хакерском духе, да еще и выставляться как принципиальные новации.
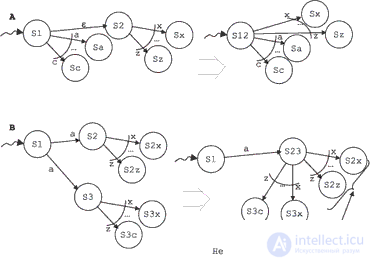
The finite automatization theorem justifies the existence of a successful calculation. But it does not give any good estimates of the change in computational complexity in the transition to deterministic search. And even if a successful calculation exists, it does not mean that it is easy to transform actions associated with transitions and that after transformation they will be at least somewhat understood. For this reason, it is often more convenient to describe the processing as non-deterministic, entrusting the solution of the task of organizing the search of variants to a programming system.
Поскольку структура программы и структура Поля зрения практически изоморфны, естественно ставить вопрос о динамическом порождении PROLOG -программ. Кроме этого высокоуровневого соображения, есть и прагматическое, которое можно извлечь из нашейпрограммы 6.3.2. В нашу программу мы были вынуждены записать и определение лабиринта.Конечно же, можно было бы прочитать с помощью встроенной функции read определение лабиринта и записать его в список, но тогда мы почти утратили бы все преимущества языкаPROLOG, не избавившись при этом ни от одного его недостатка. Гораздо естественнее иметь возможность прочитать базу данных из файла.
For this purpose, the built-in predicate consult (file [.pl]) was introduced in PROLOG. It reads sentences and facts from a file and places them at the end of the program, thereby leaving the previously given definitions of the predicates intact. With its use, our program can be rewritten as follows.
way0 (X, Y, Z): - consult (labyr), way (X, Y, Z). way (x, x, [x]). way (X, Y, [Y | Z]): - connect (U, Y), not member (Y, Z), way (X, U, Z). way (X, Y, [Y | Z]): - connect (U, Y), way (X, U, Z).Listing 6.4.1. Input Maze
Example file labyr.pl:
connect (begin, 1). connect (1, begin). connect (1,2). connect (2,3). connect (3,1). connect (3,4). connect (4, end).
Program 6.4.1 represents only the idea of a solution, but it represents this idea exclusively expressively. PROLOG is adapted to find a solution, but not to optimize it. For example, if we strive to find the optimal path in some respects, the previous program will be obscured by the particulars of the PROLOG language, which will spoil the expressiveness, and yet will not give the opportunity to solve the problem as effectively as it is done in the traditional language.
There is another class of built-in relationships that act as built-in functions, but do not require explicit activation by the is operation. These include, in particular, many list actions. Consider, for example, the append predicate (E1, E2, E3). It is correctly unified when the union of the first two lists is the third. Accordingly, it can be used to calculate any of its three arguments, if the other two are given. For example,
append (X, Y, Z)
when Z = [a, b, c, d], Y = [c, d] is unified as X = [a, b].
It is unfortunate that arithmetic functions are not implemented in PROLOG in the same way!
For the dynamic generation of facts and sentences, there are functions that parse sentences and synthesize them. Functors can be declared by metapredicates, and then some of their arguments can be sentences. Of the two most important metapredicates listed below.
The assert metapredicate (P: -P1, ..., Pn) places its argument in the PROLOG program. There are several options for it that have a new proposal or fact at the beginning or end of the program. The retract metapredicate (P: -P1, ..., Pn), on the contrary, removes from the program a sentence or fact that is unified with its argument.
They can, in particular, simulate various more efficient brute-force algorithms for working with a labyrinth, but the program to some extent loses its structure clarity and it becomes extremely difficult to debug and modify it. But efficiency, comparable with traditional methods, will not be achieved anyway.
But, for example, if you analyze a complex system of rules and are looking for a conclusion, then the result of the analysis can often be written as a file of dynamically generated sentences, and this, on the contrary, makes the program more beautiful and makes debugging easier. So it makes sense to use a dynamic generation in the case when the program first collects and analyzes information, and only then begins to act. And the product, mixed with actions, is the shortest way to the failure of the program, and should be considered as hacking.
Then, after using dynamically generated facts or sentences, they can be removed from the program using the predicate
retractall (Name / Arity)
This predicate removes all sentences and facts that speak of the arity Arity's predicate Name. Naturally, this only removes the definition. If you used it, then you need to work to remove also using sentences. Therefore, it is better to remove predicates by whole meaningfully related groups, and to concentrate all such deletions in one sentence for each group.
Dynamic generation of programs is an extremely powerful method, when applied in a suitable setting and correctly, and extremely dangerous, when applied in an inappropriate environment or at least a little incorrectly. In traditional languages, it is strongly discouraged. There he (because of so many practical failures) has an odious reputation. But this reputation is primarily due to the fact that such a risky and beautiful method requires a high elaboration of ideas, and in traditional programming we are trying to use it, we are forced to work through the silliest technical problems (build a lot of backups , see the dictionary).
Attention !
In new versions of the PROLOG language , predicates that you intend to dynamically modify must be declared . For example, dynamic (connect).
To check the types of terms there are, in particular, the following built-in predicates.
For the analysis and construction of terms there are, in particular, the following predicates.
Examples
? - send (hello, X) = .. List. List = [send, hello, X] ? - Term = .. [send, hello, X] Term = send (hello, X)
free_variables (Term, List) List is unified as a list of new variables, each of which is equal to the free term Term.
atom_codes (Atom, String) Convert an atom to a string and vice versa.
Many of the implementations of the PROLOG language include a sweep package that allows for a partial calculation of the PROLOG program.
In many cases, even in a search program, it is necessary to perform calculations. In the PROLOG language there is a way to calculate the value of the arguments. These are so-called built-in functions that can be replaced with their value if their argument is known. Such functions are, in particular, numerical arithmetic operations. Note that even the built-in function is not calculated until an explicit signal is given. In your program, for example, the expression 1 + 1 + 1 can accumulate as the value of a variable, but it will not be equal to 3.
To organize the calculation, there is a special relation X is E. In this regard, E is an expression that, after substituting the current values of variables, is specified 6 in the composition of built-in functions of constant arguments. This composition is calculated, and the variable X is unified as its value.
Thus, you can gradually accumulate calculations, and then at the right time to make them. See an example.
? - assert (a (1 + 1)). Yes ? - assert (b (2 * 2)). Yes ? - a (X), b (Y), Z is X + Y. X = 1 + 1 Y = 2 * 2 Z = 6
Attention !
is not an assignment! In order to verify this, execute the simplest sentence of the PROLOG language:
? - X is 1, X is X + 1.
It is best and most natural to enter data into the PROLOG program that fully complies with the syntax of sentences and facts of the language. If the data file is not very large, then for input it suffices to use the consult predicate already described by us.
Of course, there is a more traditional input-output system. We describe its basic features.
open (SrcDest, Mode, Stream, Options)
Open file SrcDes is an atom containing the file name in the Unix notation. Mode can be read, write, append or update. The last two methods of opening are used, respectively, for adding to an existing file and for partial rewriting it. Stream is either a variable, and then an integer is assigned to it, which serves to identify the file, or an atom, and then it is used inside the program by the file name. Options can be omitted, among them one option is important: type (binary), which allows you to write codes to a binary file. Options form a list.
Of course, it is possible to manually set the current position within the file:
seek (Stream, Offset, Method, NewLocation)
Method is a reference position method. bof counts it from the beginning of the file, current from the current point, eof from the end. The NewLocation variable is unified with the new position, which is necessarily counted from the beginning.
The predicate close (Stream) does not require comments.
read (Stream, Term)
Term variable is unified with term read from Stream.
read_clause (Stream, Term)
A sentence is being read. By default, users are warned about variables that are missing in the head and are only once present in the tail.
read_term (Stream, Term, Options)
Similar to read, but allows you to set a number of possibilities that govern the representation of a term. See more details in the documentation of the specific PROLOG system.
writeq (Stream, Term)
Term is written in Stream, quotes and brackets are inserted where necessary.
write_canonical (Stream, Term)
Term is written to Stream in such a way that any PROLOG program reads it, and not just you and your program to your system.
There is a way to read and write characters, and through them strings and stuff, but this is so primitive and ugly that you can give practical advice:
Attention !
If you need to enter into the PROLOG file of a foreign language or just the usual format, or derive from it in the format prescribed for you that does not fit into the system of terms, write an adapter on Refal or Perl .
Nonetheless, here is a minimal (and almost complete) list of predicates of character and binary input and output.
get_byte (stream, byte)
Byte is treated as an integer and is unified with the next byte of the input stream. The end of the file is read as -1.
get_char (Stream, Char)
Similarly, but the next byte is treated as an atom name consisting of one character. The end of the file is unified with the end_of_file atom. Russian letters, spaces and other non-standard characters can cause trouble.
get (stream, char)
Likewise, but invisible characters are skipped.
skip (Stream, Char)
Skip everything until the Char character or the end of the file is encountered. The very first Char entry will also be skipped.
put (Stream, Char)
Output one character or byte. Char is unified either as an integer from the range [0, 255], or as an atom with the name of one character.
nl (+ stream)
Print the line break.
Comments
To leave a comment
Programming Styles and Techniques
Terms: Programming Styles and Techniques