Lecture
If the metric space is not complete, then its completion exists. To introduce this completion, we present a number of definitions. Let there exist two metric spaces (X, d), (Y, p) and f is a bijection of X onto Y.
Definition 5 . A bijection f is called an isometric isomorphism if p (f (x), f (y)) = d (x, y).
Two metric spaces isometrically isomorphic to each other are identified.
For example, the spaces C [0, 1] and C [0, 2] of continuous functions on the segments [0, 1] and [0, 2], respectively, are isometric. Isometric isomorphism between their elements can be established by the formula
C [0, 1] x (t) y (t) = x ( ) C [0, 2]. 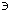
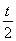
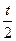
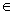
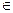
Definition 6 . Let (X, d) be a metric space and Y Ì X. A set Y is called everywhere dense in X if for " e > 0, " x Î X $ y Î Y: d (x, y) < e .
Theorem 1. Let an incomplete metric space (X, d) be given, then there exists a complete metric space ( Y , p ) and its everywhere dense subspace Y 0 such that (X, d) is isometrically isomorphic to (Y 0 , p ).
Evidence. Let {x n } and {y n } be fundamental sequences in X. We assume that {x n } ~ {y n } Û d (x n , y n ) = 0 (the properties of the equivalence relation are easily verified). Let [x n ] be an equivalence class, and Y be the set of all equivalence classes of fundamental sequences. We put r ([x n ], [y n ]) = d (x n , y n ). 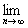
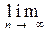
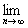
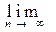
To prove the correctness of this definition, it is necessary to show: 1) the existence of the limit, 2) its independence from the choice of elements from the equivalence class, 3) the fulfillment of the metric axioms.
1) It follows from the quadrangle inequality that | d (x n , y n ) - d (x m , y m ) | £ d (x n , x m ) + d (y n , y m ). Since the sequence {x n } and {y n } are fundamental, for " e > 0 $ N: " n, m ³ N d (x n , x m ) < e / 2 and d (y n , y m ) < e / 2. We denote by a n = d (x n , y n ). It follows from the inequalities obtained above that for " e > 0 $ N: " n, m ³ N we have | a n - a m | < e and, hence, the sequence a n is fundamental, that is, there is a limit of this numerical sequence. Thus, the desired limit exists and the metric r ([x n ], [y n ]) = d (x n , y n ) is defined. 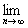
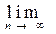
2) Let us prove that this definition does not depend on the choice of a representative of the equivalence class. Let { x n } , { x * n } Î [x n ], { y n } , { y * n } Î [y n ]. Then d (x * n , y * n ) £ d (x * n , x n ) + d (x n , y n ) + d (y n , y * n ). By the definition of equivalence classes, we have d (x * 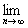
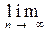 n, x n ) = 0 and d (y *
n, x n ) = 0 and d (y * 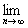
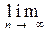 n , y n ) = 0. Therefore, d (x * n , y * n )
n , y n ) = 0. Therefore, d (x * n , y * n ) 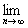
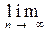 £ d (x n , y n ). The last inequality was established for arbitrary representatives of the equivalence class. Then, swapping x n and x * n , y n and y * n , we get the opposite inequality. So d (x * n , y * n ) = d ( x n , y n ).
£ d (x n , y n ). The last inequality was established for arbitrary representatives of the equivalence class. Then, swapping x n and x * n , y n and y * n , we get the opposite inequality. So d (x * n , y * n ) = d ( x n , y n ). 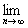
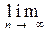
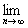
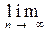
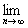
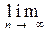
3) The axioms of the metric are easily proved using the passage to the limit.
Thus, we have established that (Y, p) is a metric space. Let us prove that it is complete. Let {[x n ] ( m ) } be a fundamental sequence in Y. We must prove that [x n ] ( m ) ® [x n ] (0) Î Y. Let {x n ( m ) } Î [x n ] ( m ) . Since for any m the sequences {x n ( m ) } are fundamental, then for " р $ k p : " n ³ k p
d (x n (p) , ) <1 / p. (1) 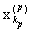
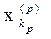
Let's build the sequence { }. We have 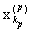
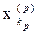
d ( , ) £ d ( , x m (p) ) + d (x m (p) , x m (n) ) + d (x m (n) , ). 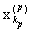
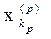
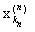
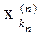
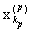
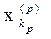
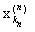
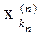
By virtue of inequality (1), due to the choice of m , k p , k n, it is possible to make the first and third terms on the right-hand side of this inequality less than any predetermined number. Since {[x n ] ( m ) } is a fundamental sequence, it follows that 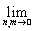
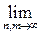 r ([x k ] ( m ) , [x k ] ( n ) ) = 0. From the definition of the metric r on Y r ([x k ] ( m ) , [ x k ] ( n ) ) = d (x
r ([x k ] ( m ) , [x k ] ( n ) ) = 0. From the definition of the metric r on Y r ([x k ] ( m ) , [ x k ] ( n ) ) = d (x 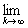
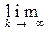 k ( m ) , x k ( n ) ) it follows that the second term can be made less than any predetermined number. Thus, the sequence { } is fundamental in X. We denote its equivalence class by [x n ] (0) . Let us show that [x
k ( m ) , x k ( n ) ) it follows that the second term can be made less than any predetermined number. Thus, the sequence { } is fundamental in X. We denote its equivalence class by [x n ] (0) . Let us show that [x 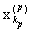
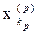 k ] ( m ) ® [x n ] (0) . Obviously, we have r ([x n ] (0) , [x k ] ( m ) ) = d
k ] ( m ) ® [x n ] (0) . Obviously, we have r ([x n ] (0) , [x k ] ( m ) ) = d 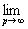
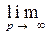 ( ,
( , 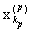
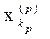 x p ( m ) ) £ d ( , ) + d ( , x p ( m ) ) < d ( , ) + 1 / m . The last limit in the inequality, due to the fundamental nature of the sequence, can be made by choosing m arbitrarily small. This means that [x k ] ( m ) ® [x n ] (0) to Y .
x p ( m ) ) £ d ( , ) + d ( , x p ( m ) ) < d ( , ) + 1 / m . The last limit in the inequality, due to the fundamental nature of the sequence, can be made by choosing m arbitrarily small. This means that [x k ] ( m ) ® [x n ] (0) to Y . 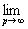
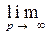
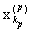
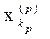
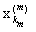
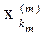
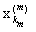
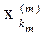
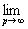
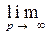
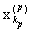
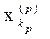
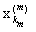
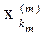
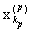
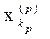
Consider [x n = x ] - a stationary fundamental sequence, x Î X, generating the equivalence class [x]. Let Y 0 denote the set of all equivalence classes of stationary sequences in X. Let us prove that Y 0 is isometrically isomorphic to X.
Let x Î X. Then this element corresponds to the stationary fundamental sequence [x] Î Y 0 . Obviously, such a correspondence is a surjection. Let us prove that this is also an injection. Let x ¹ y. Then
r ([x], [y]) = lim d (x, y) ¹ 0 Þ r ([x], [y]) ¹ 0 Þ [x] ¹ [y].
Thus, this mapping is a bijection, and r ([x], [y]) = lim d (x, y) = d (x, y) (isometry).
Let [x n ] Î Y. Then {x n } is a fundamental sequence in X, that is, for " e > 0 $ s : d ( x p , x m ) < e for all p , m > s . Construct a stationary sequence { x = x s }. Then [x] Î Y 0 and p ([x], [x k ]) = d ( x s , x k ) By the choice 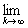
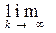 s for sufficiently large k , the inequality d ( x s , x k ) < e holds . This shows that Y 0 is dense in the space Y and the proof of the theorem is completed.
s for sufficiently large k , the inequality d ( x s , x k ) < e holds . This shows that Y 0 is dense in the space Y and the proof of the theorem is completed.
Comments
To leave a comment
Functional analysis
Terms: Functional analysis