Lecture
In the metric space, the concept of convergence of a sequence is introduced . Let (X, d ) be a metric space.
Definition 1. They say that x n Î X converges to x Î X (x n ® x; ) if d (x n , x) 
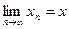 ® 0 as n ® ¥ .
® 0 as n ® ¥ .
The concept of convergence can also be formulated in the language " e - n ". For " e > 0 $ n 0 ( e ): for " n ³ n 0 the inequality d (x n , x) < e is true .
Lemma 1. If a sequence converges in a metric space, then its limit is unique.
Evidence. Let x n ® a, x n ® b . Applying the triangle inequality, we get: d ( a, b ) £ d ( a, x n ) + d ( x n , b ). Both terms on the right side tend to zero. Since d ( a, b ) non-negative and is independent of n , then the well-known theorems about the transition to the limit in the inequalities obtain d ( a, b ) = 0, and then the properties of the metric and = b , as required to prove.
Definition 2. A sequence x n of elements of a metric space X is called bounded if there is a ball S ( y , r ) to which all the members of the sequence belong.
Lemma 2. If a sequence converges in a metric space, then it is bounded.
Evidence. The assertion easily follows from the definition of a convergent sequence, if we note that if x n ® x, then for " fixed e > 0 there is n 0 for which x n Î S ( x , e ) for all n ³ n 0. Consequently, all the members of the sequence, with the exception of a finite number, fall into the neighborhood of S ( x , e ) Since any finite set of elements is always bounded, this already implies the boundedness of the entire sequence.
Consequence. If a sequence {x n } of points from X converges to a point x Î X, then the numbers d (x n , y) are bounded for any fixed point in the space X.
Lemma 3. If x n → x, y n → y, then d (x n , y n ) → d (x, y) (in other words, the metric is a continuous function of its arguments).
Evidence. By the quadrilateral inequality
| d (x, y) - d (x n , y n ) | 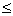
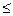 d (x, x n ) + d (y, y n ).
d (x, x n ) + d (y, y n ).
Hence, passing to the limit as n → we easily obtain the assertion of the lemma. 
In a metric space, the limit points for a set are those points x 0 for which there is a sequence of points x n of the set converging to x 0 . The closed ball S [a, r] is a closed set. Indeed, let x n S [a, r] and x n → x 0 . Then d (x n , a) r, and as n → this inequality in the limit gives d (x 0 , a) r, i.e. x 0 S [a, r]. And since each limit point of the ball is the limit of some sequence of points of the ball, the closedness of the ball is proved. 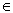
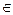
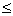
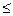
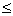
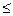
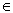
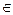
Let us clarify the specific meaning of convergence in the metric spaces R n , C [a, b], l 2 and m.
Example 1. Let X = R n . If x k → x 0 , where x k = {ξ 1 (k) , ..., ξ n (k) } and x 0 = {ξ 1 (0) , ..., ξ n (0) }, then
d (x k , x 0 ) = → 0 as k → ∞. 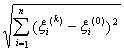
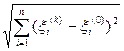
But by virtue of easily verified inequalities
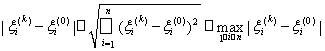
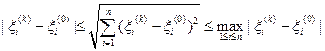 ,
,
valid for any i , this is possible if and only if ξ i ( k ) → ξ i (0) , i = 1, ..., n, as k → ∞.
Hence it follows that convergence in R n is the convergence of the coordinates of the points of the sequence to the corresponding coordinates of the point - limit, i.e. convergence in R n is convergence in coordinates .
Example 2. Let X = C [ a , b ]. If {x n (t)} C [ a , b ] converges to x 0 (t) C [ a , b ], then 
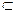
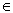
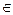
d (x n , x 0 ) = | x n (t) - x 0 (t) | → 0 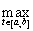
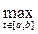
or otherwise: ε> 0 N: n> N => 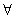
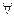
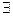
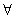
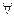 | x n (t) - x 0 (t) | <ε. This condition is equivalent to the condition that n> N => | x n (t) - x 0 (t) | <ε t [ a , b ]. But this means uniform convergence of the sequence {x n (t)} to x 0 (t). Thus, the convergence in the space С [ a , b ] is the uniform convergence of the functional sequence {x n (t)}.
| x n (t) - x 0 (t) | <ε. This condition is equivalent to the condition that n> N => | x n (t) - x 0 (t) | <ε t [ a , b ]. But this means uniform convergence of the sequence {x n (t)} to x 0 (t). Thus, the convergence in the space С [ a , b ] is the uniform convergence of the functional sequence {x n (t)}. 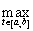
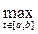
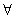
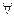
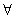
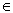
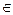
Example 3. Let X = l 2 . It can be shown that the convergence of the sequence {x n } l 2 to x 0 l 2 , where x n = {ξ i (n) }, x 0 = {ξ i (0) } means that 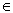
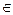
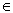
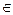
1) ξ i (n) → ξ i (0) for i = 1,2, ...
2) ε> 0 N: <ε for all n = 1,2, ..... 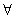
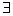
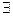
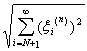
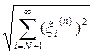
Thus, convergence in l 2 contains stronger requirements than convergence in coordinates. Let us show this with an example showing that in l 2 the convergence in coordinates does not imply the convergence of a sequence of points in l 2 .
In the space l 2 we take the sequence e m = {ξ i (m) }, where ξ i (m) = δ mi (the Kronecker symbol). We take x 0 = (0, 0,…, 0,…) l 2 . Then the sequence {e m } in coordinates tends to the point x 0 . However, 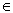
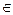 d (e m , x 0 ) = 1, therefore {e m } does not tend to x 0 in the metric.
d (e m , x 0 ) = 1, therefore {e m } does not tend to x 0 in the metric.
Example 4. Let X = m . The convergence of the sequence x n = {ξ 1 (n) ,…, ξ n (n) ,…} m to the element x 0 = {ξ 1 (0) ,…, ξ n (0) ,…} means uniform convergence in coordinates , i.e. 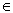
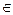 " ε> 0 N:
" ε> 0 N: 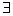
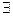 " n> N Þ | ξ i ( n ) - ξ i (0) | <ε " i = 1,2, ... This is proved in the same way as in Example 2.
" n> N Þ | ξ i ( n ) - ξ i (0) | <ε " i = 1,2, ... This is proved in the same way as in Example 2.
It can be shown that in the metric space s of all numerical sequences the convergence in the metric coincides with the convergence in the coordinates.
Definition 3. A sequence x n Î X is called a fundamental sequence if for " e > 0 $ N: d (x n , x m ) < e if n, m ³ N.
Lemma 4 (on the convergence of sequences ). Let { x n } be a sequence from the metric space X. The following conditions are equivalent:
1. { x n } - converges to x ;
2. Any subsequence { x n } converges to x ;
3. For any subsequence { } there is a subsequence { } converging to x; 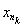
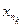


4 . { x n } is fundamental and any subsequence { } converges to x ; 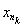
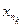
5. { x n } is fundamental and there is a subsequence { } converging to x . 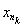
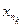
Evidence.
1. Þ 2. and 2. Þ 3. Standard statements from mathematical analysis: a subsequence of a converging sequence converges to the same limit: the proof is absolutely similar.
4. Þ 5. Obvious.
3. Þ 4. follows from 5. Þ 1. Indeed, if 5. Þ 1. has already been proved, then by the conditions of item 4. the subsequence { } is fundamental, but by item 3 it has a subsequence converging to x . Then from 5. 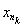
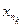 Þ 1. it follows that { } itself converges to x .
Þ 1. it follows that { } itself converges to x . 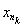
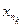
5. Þ 1. Let { x n } be a fundamental sequence and be its subsequence converging to x . For 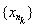
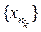 " e > 0 $ N 1 : d ( x p , x m ) < e , p, m> N 1. Putting here m = n k , n k ³ N 1 , k ³ N, we have d ( x p , ) < e . Consequently, d ( x , x p ) £
" e > 0 $ N 1 : d ( x p , x m ) < e , p, m> N 1. Putting here m = n k , n k ³ N 1 , k ³ N, we have d ( x p , ) < e . Consequently, d ( x , x p ) £ 
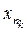 d ( x , ) + d ( ,
d ( x , ) + d ( , 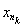
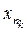
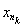
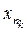 x p ) £ e + e £ 2 e (p> N 1 ) and x p ® x Î H.
x p ) £ e + e £ 2 e (p> N 1 ) and x p ® x Î H.
Definition 4. A metric space X is called complete if any fundamental sequence in this space converges to an element of this space.
Example 5. For the case of R n - Euclidean n-dimensional space - the completeness follows from the Cauchy criterion for the existence of the limit of the sequence of points of this space.
Example 6. Consider the space C [0, 1] introduced above. By the definition of the fundamental sequence { x n } and the metric for " e > 0 $ N: < e " n, m ³ N. If we fix t, then x n (t) will be an ordinary numerical fundamental sequence, which exists due to the criterion Cauchy is the pointwise limit x ( t ). Passing to the pointwise limit in the inequality, which is true for any t Î [0, 1] as m ® ¥, we obtain £ e for " n ³ 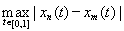
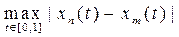
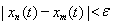
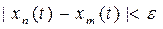
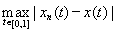
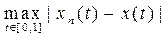 Of N . Thus, the sequence x n ( t ) converges uniformly on the segment [0, 1] to the function x ( t ). Then, by the Weierstrass theorem on the continuity of the uniform limit of continuous functions, x (t) is a continuous function on the interval [0, 1]. Hence C [0, 1] is a complete space.
Of N . Thus, the sequence x n ( t ) converges uniformly on the segment [0, 1] to the function x ( t ). Then, by the Weierstrass theorem on the continuity of the uniform limit of continuous functions, x (t) is a continuous function on the interval [0, 1]. Hence C [0, 1] is a complete space.
Example 7. On the set C [0, 1], you can introduce another metric, for example:
d (x, y) = 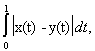
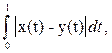
but in this case the space will not be complete. To prove this, it suffices to consider the following sequence of continuous functions:
x n ( t ) = 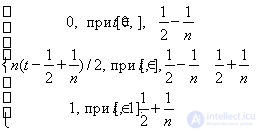
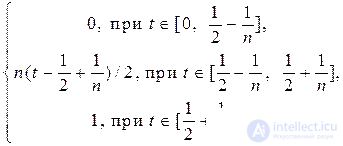
Show that this sequence is fundamental in the reduced metric (use the geometric meaning of the definite integral), but converges to a discontinuous function.
Example 8. Let us show the completeness of the space l 2 . Let the sequence x ( m ) = ( x 1 ( m ) , x 2 ( m ) , ..., x n ( m ) , ....), m = 1, 2, .... is fundamental in l 2 . Therefore, for an arbitrarily chosen e > 0, there exists a number n 0 such that for all k , m ³ n 0 , the inequality < 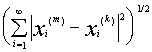
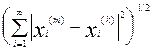 e . From the inequality | x n ( m ) - x n ( k ) | £ , valid for any n Î N , it follows that the sequence { x n ( m ) } is fundamental in the space R and hence its convergence x n ( m ) ® x n as m ® ¥ . Moving on in the obvious inequality
e . From the inequality | x n ( m ) - x n ( k ) | £ , valid for any n Î N , it follows that the sequence { x n ( m ) } is fundamental in the space R and hence its convergence x n ( m ) ® x n as m ® ¥ . Moving on in the obvious inequality 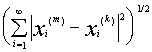
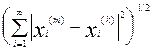
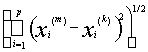
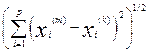 < e
< e
for a fixed m to the limit first as k ® ¥ , then as p ® ¥ , we obtain the inequality
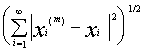
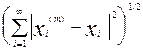 £ e .
£ e .
From the triangle inequality

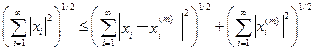
it follows that x belongs to l 2 . The previous inequality implies the convergence of x ( m ) to x in l 2 .
Comments
To leave a comment
Functional analysis
Terms: Functional analysis