6 . Interior points of the set, interior. Set boundary

F Consider the more d va in azhnyh understood Ia, with knitted with claim onyatiem about the vicinity of xS.

14. Determination of T points x Î A n be ordered internal point m nozhestva A, if n EIDET t Which e e a vicinity of xS O ( x ), that O ( x ) Ì A .

Set in Cex in Cored oil t ochek m nozhestva A is called the interior of A and denoted Int A .

Example 18 . N ust A = [0 , 1] - about trezok in eschestvennoy straight , t hen Int [0, 1] = (0 , 1 ).

Operation Int d voystvenna about perazim circuit hours then at idno of th e with voystv, f ormuliruemyh in the next t eoreme.

Theorem 7. For n yubogo set A Ì X have:

1 ) Int A - TCI rytoe set,

2 ) I nt A - the largest open set, with obsessed in A ;

3) (A - about eopen) Û ( I nt A = A );

4) ( x Î I nt A ) Û ( x Î A and x n e is the limit point d A X \ A);

5) ` = X \ I nt A.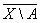

Evidence. With voystva 1 ) - 3 ) n ochti obvious. Check them n For example, with voystvo 1 ). P ust x Î Int A ; t hen there t Which open to the vicinity of xS O ( x ) t points x , h is O ( x ) Ì A. But O ( x ) is open, i.e. each point internal to A and hence O ( x ) Ì Int A. P oetomu by Theorem 2 Int A - about eopen m nozhestvo.

Let 's check with property 4 ). E If x Î Int A, r o, of chevidno, x Î A and x Ï ( X \ A) '. On of inverse: e If x Î A and x Ï ( X \ A) ' m a n EIDET vicinity spine U ( x ) Ì A , with been consistent, x Î Int A ...

By a voystva 5 ) n to gives h itatelyam.

The next important item onyatiya - concepts g ranichnoy t glasses and g ranitsy m nozhestva A , are associated with INT uitivnym n redstavleniem of "partition" of tdelyayuschey of the blasts.

Definition 15 . T ranichnoy point oh m nozhestva A is a point x of X topological space, which has the property that every neighborhood of the intersection G ( x ) with the set A and set X \ A is not empty. T ranitsey d A m nozhestva A n AZOV plurality of boundary points A.

Thus on Brazier, x Î d A t hen and t nly t hen, a hen to ach okres tnost x comprises m point each to ak and of A , T ak and and of X \ A.

Example 19. n ust X = R 1 , and A = (0, 1 ) T hen d A = {0, 1} - m nozhestvo and h d Vuh m ochek: 0 and 1 .

We got a set operation again. E e with ligature with ACTIVITY iyami of amykaniya and Int in yyasnyaet with sending this t eorema.

Theorem 8. A la L yubogo A Ì X and Lev Mey :

1 ) q A = ` A Ç ;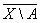

2 ) q A = ` A \ Int A;

3 ) ` A = A È d A ;

4 ) Int A = A \ d A;

5 ) ( A is closed o ) Û ( dA Ì A );

6) ( A of eopen) Û ( ( d A) Į A = Æ ).

Evidence. D will provide n ome and h e is silent at the evidence supporting, on becoming e THER as in EXERCISE. 1 ) n ust x Î d A . T hen in any env estnosti O ( x ) m points x n aydutsya m points x 1 , x 2 t Which, h then X 1 Î A, x 2 Î X \ A. On tsyuda x Î ` Aand x Î ,m . e . 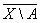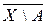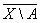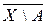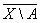x Î ` A Ç .About of inverse: e If x Î ` A Į ,tons of x Î ` And , x Î and then for any neighborhood O ( x ) the intersection of G ( x ) Į A ¹ 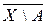Æ and O ( x ) Ç (X / A) ¹ Æ . Hence x is a boundary point.

2) C ccording to 1) dA Ì ` A. On the other hand, if x Î IntA , there is a neighborhood of this point, which lies completely in A and hence does not intersect with the X / A, i.e. x Ï dA . Hence dA Ì ` A \ IntA . Conversely, if x Î ` A \ IntA , then the intersection of any neighborhood of the point with A will not be empty (belonging to the closure), but also the intersection of any neighborhood with X \ A will not be empty, since the point is not inside.

3) T ak to ak Int A Ì ` A , T on and h 2 ) with examines ` A = I nt A È d A Ì A È d A ; t ak to ak e A Ì ` A and A Ì ` And , so on A È etc. A Ì ` And