Lecture
The concept of a set was studied by students in the course of mathematical analysis. Here we recall the basic concepts and terms from this theory.
The concept of a set is so general that it is difficult to give a formal definition for it (i.e., reduce it to other concepts, simpler and clearer).
We will consider sets of numbers, sets of points, sets of lines, sets of functions, etc. The sets will be denoted by capital letters: A, B, M, N , etc. The objects that make up the set are called the elements of the set, we will denote them by small letters. The notation (or ) means that a is an element of the set A ; recording means that a is not an element of the set A . The notation (or ) means that each element of the set A is an element of the set B ; in this case, the set A is called a subset of the set B 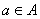
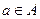
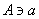
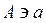
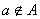
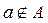
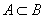
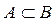
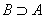
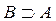 ... If there are inclusions , B
... If there are inclusions , B 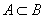
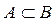 Ì A , then this means that the sets A and B consist of the same elements and, therefore, coincide with each other. This fact is written by the equality A = B. There is one special set, the so-called empty set, which does not contain a single element. The empty set is denoted by the symbol Æ .
Ì A , then this means that the sets A and B consist of the same elements and, therefore, coincide with each other. This fact is written by the equality A = B. There is one special set, the so-called empty set, which does not contain a single element. The empty set is denoted by the symbol Æ .
Consider the simplest operations that can be performed on sets: union, intersection, and complement.
Let a family of sets { A a } a , where the subscript a ranges over a plurality of T . Consider the collection of all elements, each of which belongs to at least one of the sets A a . This collection is a new set, which is called the union of sets A a and is denoted . Note that if any element is included in several sets, then it is included in the union of these sets only once. According to the axioms of set theory, an empty set is a subset of any set. 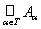
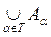
Suppose again given collection of sets { A a } a Î T . The set consisting of those and only those elements that belong to each of the specified sets is called the intersection of sets and is denoted by . 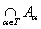
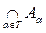
If for a ¹ b , a , b Î Т the equality A a Ç A b = Æ holds , then the union is called disjoint and is denoted . 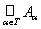
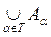
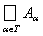
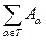
From the definition of union and intersection of sets, it can be seen that these operations have the property of commutativity and associativity. It is also easy to show that the following distributivity law holds = 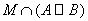
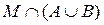
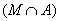
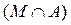 È .
È . 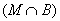
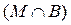
Let sets A and B be given . Elements of the set A that do not belong to B form a set called the difference of the sets A and B and denoted by A - B or A \ B. It is easy to see that A \ B = A \ . 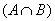
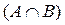
Let's introduce one more concept. If B is a subset of A, then the difference A \ B is called the complement of the set B to the set A. Note the obvious formula: if , then . Note that this formula is not true at all for two arbitrary sets A and B. 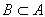
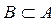
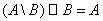
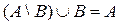
Of the more complex formulas, we note the following, which will often be encountered.
Theorem (duality principle) . Let a system of sets A α 
 and a set Ω be given , with A α . Then
and a set Ω be given , with A α . Then 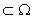
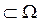
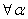
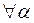
È a ( W - А a ) = W - ( Ç a А a );
Ç a ( W - А a ) = W - ( È a А a ).
A mapping φ of a set M 1 into a set M 2 (notation φ: M 1 ® M 2 ) is a law φ such that each element x Î M 1 is associated with one and only one element y Î M 2 , denoted by φ (x ) and called the image of the element x under the mapping φ.
The collection of all those elements a Î M 1 , whose image is a given element b Î M 2 , is called the inverse image of the element b under the map φ: M 1 ® M 2 and is denoted by φ -1 (b). Thus, φ -1 (b) = {a Î M 1 : j (a) = b}.
Let A be some subset of M 1 ; the collection {φ (a): a Î A} of all elements of the form φ (a), where a Î A, is called the image of A and is denoted by φ (A). In turn, for each set B M 2 , its full preimage 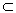
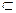 φ -1 (B) is defined , as the set of all those elements from M 1 whose images belong to B, i.e. φ -1 (B) = {a Î M 1 : j (a) Î B}
φ -1 (B) is defined , as the set of all those elements from M 1 whose images belong to B, i.e. φ -1 (B) = {a Î M 1 : j (a) Î B}
Recall that a mapping φ of a set M 1 into a set M 2 is called a surjection if φ (M 1 ) = M 2 .
If for any two different elements x 1 and x 2 from M 1 their images y 1 = φ (x 1 ) and y 2 = φ (x 2 ) are also different, then φ is called an injection . The mapping φ: M 1 M 2 , which is both a surjection and an injection, is called a bijection, 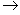
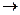 or a one-to-one correspondence between M 1 and M 2 .
or a one-to-one correspondence between M 1 and M 2 .
The following basic properties of mappings take place:
Preimage theorem . The preimage of the union or intersection of two sets is equal to the union or intersection of their preimages, respectively:
φ -1 ( A B ) = φ -1 ( A ) φ -1 ( B ), 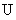
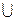
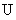
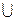
φ -1 ( A B ) = φ -1 ( A ) φ -1 ( B ). 
Image theorem . The image of the union of two sets is equal to the union of their images:
φ (A B) = φ (A) φ (B). 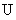
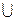
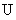
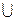
Note that the image of the intersection of two sets, generally speaking, does not coincide with the intersection of their images.
A mapping I M : M ® M is called the identity (or unit) mapping of the set M if I M (x) = x, " x Î M.
Let mappings φ: M 1 ® M 2 and ψ: M 2 ® M 3 be given , then the composition of the mappings φ and ψ 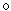
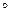 can be defined as the mapping ψ φ: M 1 ® M 3 defined by the formula (ψ φ) (x) = ψ (φ (x)), x
can be defined as the mapping ψ φ: M 1 ® M 3 defined by the formula (ψ φ) (x) = ψ (φ (x)), x 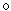
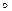
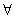
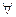 Î M 1 .
Î M 1 .
A mapping φ: M 1 M 2 is called invertible 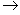
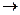 if there exists a mapping ψ: M 2 M 1 such that the following relations hold:
if there exists a mapping ψ: M 2 M 1 such that the following relations hold: 
φ ψ = I M2 
ψ φ = I M1 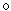
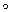
In this case, the mapping ψ is called inverse to the mapping φ and is denoted by φ -1 .
The uniqueness theorem for the converse . If the mapping φ: М 1 → М 2 is invertible, then the inverse mapping φ -1 is unique.
The following criterion for the invertibility of a mapping holds.
The theorem on the existence of the converse . The mapping φ: М 1 → М 2 is invertible if and only if φ is bijective.
In this case, the inverse mapping φ -1 : М 2 → М 1 is defined (unambiguously) as follows: the image of the element y M 2 under the mapping φ -1 will be such an element x M 1 , which, under the mapping φ, goes into the element y. In other words: φ -1 (y) = x 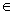
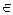
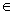
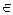 Û φ (x) = y.
Û φ (x) = y.
Comments
To leave a comment
Functional analysis
Terms: Functional analysis