Lecture
Definition 7 . Let a metric space (X, d) and a sequence of closed balls S [x k , r k ] be given. Such a system of balls is called nested if:
1. S [x 1 , r 1 ] Q S [x 2 , r 2 ] Q ...;
2. 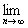
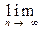 r n = 0.
r n = 0.
Theorem 2. X - a metric space is complete if and only if any embedded system of balls in X has a non-empty intersection (there is a unique point belonging to each ball of the system).
Necessity. By 2) the condition for the embedded system for " e > 0 $ N: 0 <r k < e if k ³ N. Consider the sequence of centers of these balls. By condition 1) x k Î S [x N , r N ], if k ³ N, that is, d (x N , x k ) £ r N < e . Then, by the triangle inequality, we easily obtain d (x n , x k ) <2 e for all n , The k ³ of N . Thus, {x k } is a fundamental sequence in the space X. Due to the completeness of this space, there exists x = x n . By 1) the condition x n Î S [x k , r k ] for n ³ k and x n ® x. Since the ball S [x k , r k ] is closed , this means that x Î S [x k , r k ] and this is true for arbitrary k 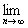
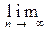 ... Hence, x belongs to the intersection of these balls.
... Hence, x belongs to the intersection of these balls.
Using property 2) of the embedded system of balls and the triangle inequality for the metric, show yourself the uniqueness of this point.
Adequacy. Take y k Î X - an arbitrary fundamental sequence in the space X. Then for " e k = (1/2) k $ n k : d ( , y m ) <(1/2) k for m ³ n k . By the sequence { } we construct the following system of nested balls . To check the nesting of this system, it is obviously sufficient to check only the first condition in the definition. Let y Î . Then d ( , y) £ d ( , ) + d ( , y) £ (1/2) 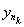
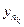
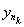
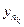
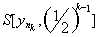
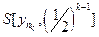
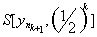
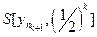
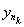
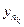
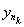
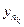
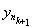
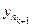
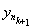
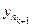 k + (1/2) k £ (1/2) k -1 , i.e. have Î and Ì .
k + (1/2) k £ (1/2) k -1 , i.e. have Î and Ì . 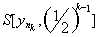
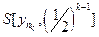
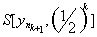
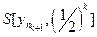
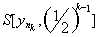
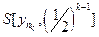
Therefore = {x 0 }. Then 0 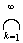
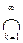
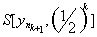
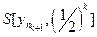 £ d ( , x 0 )
£ d ( , x 0 ) 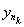
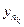 £ (1/2) k -1 , that is,
£ (1/2) k -1 , that is, 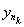
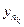 ® x 0 (k ® ¥ ). Then, by Lemma 4, the sequence { y k } itself converges to x 0 .
® x 0 (k ® ¥ ). Then, by Lemma 4, the sequence { y k } itself converges to x 0 .
The theorem is proved.
Definition 8 . The diameter of a set M of a metric space (X, d ) is the number diamM = sup d ( x , y ), where the supremum is taken over all x, y Î M.
Definition 9. A system of closed sets M n of a metric space ( X , d ) is called embedded if the following two conditions are satisfied:
1) M 1 É M 2 É M 3 É ... É M n É ... ;
2) diam M n ® 0 as n ® ¥ .
The next theorem is an analogue of Theorem 2 and is proved in exactly the same way.
Theorem 3. X - a metric space is complete if and only if any embedded system of closed sets M n in X has a non-empty intersection (there is a unique point belonging to each set of the system).
The following example shows the importance of the condition that the diameter of sets tends to zero in the definition of an embedded system.
Example 9 . In the space l 2 we put M n = { x = (0, ..., 0, x n , x n +1 , ...)} Î l 2 : = 1}. It is easy to see that these sets are closed, satisfy condition 1) and do not satisfy condition 2) (calculate the diameters of the considered sets) of Definition 9. It is quite obvious that their intersection is empty. 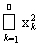
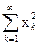
Comments
To leave a comment
Functional analysis
Terms: Functional analysis