At the beginning of bsudim n ome n onyatiya, with knitted with n PTFE coating topological n a space of. N ust r = {A} - N ome with YSTEM n odmnozhestv A m nozhestva X . On bedinenie in Cex A and z r of We denote ` r and called T elom with Istemi r .

Determination 22. With YSTEM r n be ordered n PTFE coating podprostr anstva X topological n a space of Y , e fusion ` r É X .

23. Determination of T OVOR, h then n PTFE coating r subspace X is subcovering cover r ' subspace X , e fusion to azhdy e lement r is e lementom with Istemi r '.

The ratio subcovering in leads h astichnuyu in disordered in m nozhestve in Cex claim PTFE coating subspace X . Coatings with tinuous and s to f course and whether to even hours Isla element s are referred to ootvetstvenno end and whether to even.

Particular of their assignment and hav e n PTFE coating, with tinuous and of about Access the plural of the EU ETS. Such claim PTFE coating n be ordered open .

With a voystvami about Access the n PTFE coating with knit m legged in azhnye Propert space Twa. In a ligature with e tim in ydelyayut with leduyuschie to Lassen pros transtva.

Definition 24. Let Y be a topological n space. The set X Ì Y n be ordered compactly , e fusion to a syakogo e th TCI rytogo claim PTFE coating exists a finite about eopen under n PTFE coating.

In this case, any open cover is said to contain a finite subcover.

A compact set X with an induced topology is a topological space. It is called a compact space .

Example 18 . P est X = [ a, b ] - and s R 1 . The set X to ompaktno, t ak to ak n of m eoreme Heine - Borel and h l yubogo claim PTFE coating X and ntervalami m You can in Highlight finite subcover.

Theorem 13. Every closed subset X of a compact space Y is itself compact.

Evidence. Let r = { A } - open cover X . Then, by definition inducible topology for any set of coating A r holds predstvalenie A = Ç X , where V - open sets of Y . By closed X , a plurality of Y \ X is open, and the system sets { B } È { Y \ X } forms an open cover Y . Since Y is compact, from this covering one can select a finite subcovering that contains the sets В 1, B 2 , ..., B n , and perhaps a lot of the Y \ the X . Therefore, Y = В k È ( Y \ X ). But then the set A k = B k Į X, k = 1, 2, ..., n , are a finite open cover for X . The latter means that X is a compact set.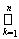

Next t eorema h Frequently n rimenyaetsya in the analysis.

Theorem l 4 . In syakoe b eskonechnoe plurality Z Ì X to ompaktnogo plurality of X is a X n redelnuyu m point each.

Evidence. N redpolozhim n rotivnoe, m . e . h then Z '= Æ . T hen ` the Z = the Z , therefore, the Z is closed, and with been consistent, and Comp Comp act. C d nother with thoron to ach r points z Î Z is not limiting assumption. Then there is a eopen of the vicinity of xS O ( z ) in X with y the word O ( z ) Ç Z = { z }. Such a vicinity of xS O ( z ) of Braz infinite claim PTFE coating n a space of Z , and z to otorrhea n Elzi in The selected to f course subcovering in claim rotivorechii with a ompaktnostyu Z .

The concept to ompaktnosti t ECHO with knit with claim onyatiem of A closed, to ak n has the following have evidence supporting.

Theorem 15. P ust X - to ompaktnoe podnozhestvo Hausdorff n a space of Y . Then X is closed.

Evidence. N ust y Î Y \ H. D A L Juba m points x Î X in a mud Hausdorffness Y exist t Which of eopen about the vicinity of xS U x ( y ), V y ( x ) t ochek y , x , h then U x ( y ) Ç V y ( x ) = Æ .

System ( V y ( x )) x Î X of Braz open claim PTFE coating X . In a mud to ompaktnosti X and s an a f course subcover ( V y ( x k )) k = 1 n . A It is easy in goes h then sets V ( X ) = V y ( x 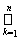the k ) and the U ( y ) = open , and n e intersect are. 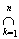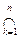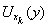T mayor of Braz, n exerted, h then a Hausdorff n a space of a ompaktnoe plurality of X and T point each, n e l ezhaschuyu in n eat m You can partition it n eperesekayuschimisya surroundings 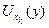U (x) and U (y ). On tsyuda following t h then d Supplement No. Y \ X of eopen, n oetomu X is closed.

Tasks

1. What is the ball S (0 , 1) m centered at point 0 = (0,0, 0,…) and radius 1.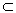

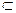
2. Let l 1 be a set of elements x of the form x = { i } 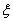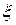, where < , with distance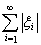

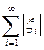
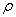
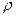(x, y) = , where y = { }.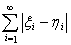

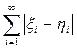
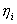
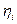
Prove that l 1 is a metric space. What is the ball S (0 , 1) in this space?

3. Show that if the set E on the line is covered with an arbitrary system of intervals, then it can be identified (no more than countable) subsystem also covers E .

4. Show that if the set E on the plane covered by an arbitrary system of circles, some of it is not more than a countable subsystem can be identified, also overlaps E .

5. We denote the set of limit points of any set A by A ′ . Construct the set A on the line so that A ″ = (A ′) ′ is not empty, but A ′ ″ is empty.

6. Prove that the set A ' (see. The task 5) is closed, whatever A .

7. It is known that A is countable. Prove that A is countable ( A is on the line).

8. A point x on the straight line is called a point condensation uncountable set A , if any neighborhood of x has innumerable points of A . Prove that every uncountable set A has condensation points.

9. The value ( x, A ) = is called the distance from point x to the set of A . Prove that for a closed set A the relation ( x, A ) = 0 and x A are equivalent; if A is not closed, then they are not equivalent.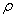

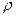
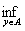
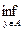
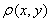
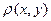
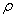
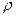
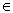
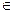
10. Prove that for any set A the collection of points x for which ( x, A ) < ε is open, and the collection of points y for which ( x, A ) ε is closed.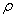

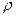
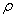
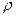
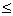
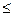
11. Immediately deduce from the definition of a closed set that any finite set of points of a metric space is closed.

12. Prove that ( A È B ) ′ = A ′ È B ′.

13. Does it follow from that A B?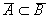

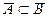
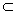
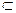
14. Show that = F , where F - all possible closed set containing M .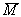

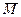
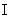
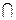
15. In the space С [ a, b ], the set M n is the collection of all polynomials of degree not exceeding n . What is it ?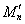

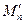
16. Prove the inclusion . Can the inclusion sign be replaced with an equal sign?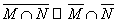

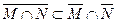
17. We denote by the set of all interior points of the set. Prove what is open.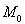

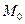
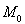
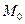
18. Let M be the set of points in space for which all coordinates are positive. Will M be open?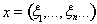

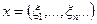
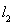
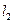
19. Let the function be defined and continuous on the whole number axis . Prove that the set of points x is open.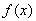

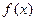
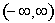
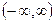
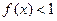
20. In space, the set A consists of functions whose value for any t belongs to a given closed set M of real numbers. Will A be closed? Will A be open if M is open?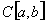

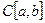
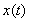
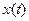
21. Prove that the set of all isolated points of a separable metric space is at most countable.

22. Show that if F is a closed set, then , generally speaking (show with an example), there may be no equality here (the zero denotes the interior).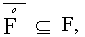

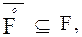
23. Is the statement true: the interior of the intersection of two sets is equal to the intersection of their interior. Is a similar statement true for the unions of two sets?

24. Prove that the boundary of each set is closed.

25. Construct on the number line a set with the following three properties: 1) all its points are isolated; 2) the exact lower bound of the distances between different points is equal to zero; 3) it has no limit points.

26. Let Φ be a function twice continuously differentiable on [0, ¥ ) that satisfies the following conditions: a) Φ (0) = 0; Ф ( x )> 0 for x > 0; b) F ¢ ( x ) ³ 0 and F ¢ ¢ ( x ) £ 0 for x ³ 0. Prove that the function r ( x , y ) = F (| x - y |) opredelyachet metric on R .