Lecture
The normal algorithm (algorithm) of Markov ( HAM , also a Markov algorithm ) is one of the standard ways of formally defining the concept of an algorithm (another well-known method is the Turing machine). The concept of a normal algorithm was introduced by A. A. Markov (the youngest) in the late 1940s in the work on the insolubility of some problems in the theory of associative computing. The traditional spelling and pronunciation of the word “algorithm” in this term also goes back to its author, who has taught many years of mathematical logic at the Faculty of Mechanics and Mathematics of Moscow State University.
The normal algorithm describes a method of rewriting strings, similar in the way of setting formal grammars. NAM is a Turing-complete language, which makes it expressively equivalent to a Turing machine and, therefore, to modern programming languages. On the basis of NAM was created functional programming language Refal.
Normal algorithms are verbal, that is, intended to be applied to words in different alphabets.
The definition of any normal algorithm consists of two parts: the definition of the alphabet of the algorithm (to the words of whose characters the algorithm will be applied) and the definition of its scheme . A scheme of a normal algorithm is called a finite ordered set of so-called substitution formulas , each of which can be simple or final . Simple substitution formulas are words of the form. 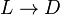 where
where 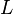 and
and 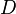 - two arbitrary words in the alphabet of the algorithm (called, respectively, the left and right sides of the substitution formula). Similarly, the final substitution formulas are called words
- two arbitrary words in the alphabet of the algorithm (called, respectively, the left and right sides of the substitution formula). Similarly, the final substitution formulas are called words 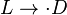 where
where 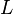 and
and 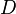 - two arbitrary words in the alphabet of the algorithm. It is assumed that the auxiliary letters
- two arbitrary words in the alphabet of the algorithm. It is assumed that the auxiliary letters  and
and  do not belong to the alphabet of the algorithm (otherwise, the other two letters should be chosen for the role played by the separator of the left and right sides).
do not belong to the alphabet of the algorithm (otherwise, the other two letters should be chosen for the role played by the separator of the left and right sides).
An example of the scheme of the normal algorithm in the five-letter alphabet 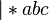 can serve as a circuit
can serve as a circuit
The process of applying a normal algorithm to an arbitrary word  in the alphabet of this algorithm is a discrete sequence of elementary steps, consisting of the following. Let be
in the alphabet of this algorithm is a discrete sequence of elementary steps, consisting of the following. Let be  - the word obtained at the previous step of the algorithm (or the original word
- the word obtained at the previous step of the algorithm (or the original word 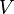 if the current step is first). If among the substitution formulas there is no such, the left part of which would be included in
if the current step is first). If among the substitution formulas there is no such, the left part of which would be included in 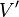 , the work of the algorithm is considered complete, and the result of this work is the word
, the work of the algorithm is considered complete, and the result of this work is the word 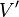 . Otherwise, among the substitution formulas, the left part of which is included in
. Otherwise, among the substitution formulas, the left part of which is included in 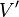 , the very first is chosen. If this substitution formula is
, the very first is chosen. If this substitution formula is 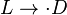 then of all the possible representations of the word
then of all the possible representations of the word 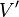 as
as  is chosen such that
is chosen such that 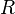 - the shortest, after which the work of the algorithm is considered complete with the result
- the shortest, after which the work of the algorithm is considered complete with the result 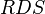 . If this substitution formula is
. If this substitution formula is 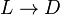 then of all the possible representations of the word
then of all the possible representations of the word 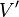 as
as 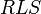 is chosen such that
is chosen such that 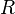 - the shortest, followed by the word
- the shortest, followed by the word 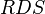 considered to be the result of the current step to be further processed in the next step.
considered to be the result of the current step to be further processed in the next step.
For example, during the process of applying the algorithm with the above scheme to the word 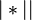 words appear consistently
words appear consistently 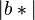 ,
, 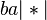 ,
, 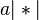 ,
, 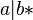 ,
, 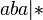 ,
, 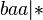 ,
, 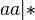 ,
, 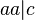 ,
, 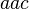 ,
, 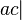 and
and 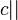 after which the algorithm terminates with the result
after which the algorithm terminates with the result 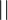 . See other examples below.
. See other examples below.
Any normal algorithm is equivalent to some Turing machine, and vice versa - any Turing machine is equivalent to some normal algorithm. A variant of the Church-Turing thesis, formulated in relation to normal algorithms, is usually called the “normalization principle”.
Normal algorithms have proven to be a convenient means for building many sections of constructive mathematics. In addition, the ideas embedded in the definition of a normal algorithm are used in a number of programming languages oriented towards the processing of symbolic information — for example, in Refal.
Using the Markov algorithm for conversions above strings.
Alphabet:
Rules:
Source line:
When the algorithm is executed, the line undergoes the following changes:
This completes the algorithm execution (since formula No. 5, which we made final, will be achieved).
This algorithm converts binary numbers to "single" (in which the record of a non-negative integer number N is a string of N sticks). For example, the binary number 101 is converted to 5 sticks: |||||.
Alphabet:
Rules:
Source line:
Performance:

Comments
To leave a comment
Theory of Automata
Terms: Theory of Automata