Lecture
The reaction of an automaton is the sequence of output signals of an automaton obtained under the influence of a certain sequence of input signals, that is, the reaction is the output word of the automaton to a specific input word.
So for an automaton in Figure 2.1, the formation of the reaction is presented in Table 2.1. The input of the machine is a sequence of input signals.  . The automaton is in the initial state
. The automaton is in the initial state 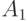 . Incoming input signal
. Incoming input signal 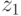 puts the machine in state
puts the machine in state 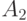 and the output signal is formed on this transition at the same discrete moment of time.
and the output signal is formed on this transition at the same discrete moment of time. 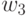 . In the second moment of time
. In the second moment of time 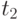 an input signal acts on the machine
an input signal acts on the machine 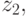 which translates the machine to the state
which translates the machine to the state 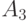 , and on this transition at the same discrete point in time
, and on this transition at the same discrete point in time 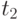 output signal is generated
output signal is generated 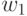 and so on. As a result, the input word
and so on. As a result, the input word  formed output word
formed output word  which is the reaction of the automaton.
which is the reaction of the automaton.
| Time t | t1 | t2 | t3 | t4 | t5 | |
|---|---|---|---|---|---|---|
| Input signals | z 1 | z 2 | z 1 | z 2 | z 2 | |
| States | a 1 | a 2 | a 3 | a 3 | a 2 | a 1 |
| Output signals | w 3 | w 1 | w 1 | w 2 | w 2 |
For Moore's automaton, the formation of a reaction occurs in a similar way, with the only difference that in Moore’s automaton, the output signal is not given at the transition of the automaton from the state  in state
in state  as in the Miles automaton, and after the automaton passed into the state
as in the Miles automaton, and after the automaton passed into the state 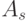 .
.
Automatic Miles  Fig.2.2 is set to its original state
Fig.2.2 is set to its original state 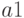 .An input is the input word:
.An input is the input word:  . As a result, the output word is formed.
. As a result, the output word is formed.  which is the reaction of the automaton (Table 2.2). Moore's gun
which is the reaction of the automaton (Table 2.2). Moore's gun  the graph, which is presented in Fig.2.3, is set to its original state
the graph, which is presented in Fig.2.3, is set to its original state 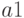 .
.
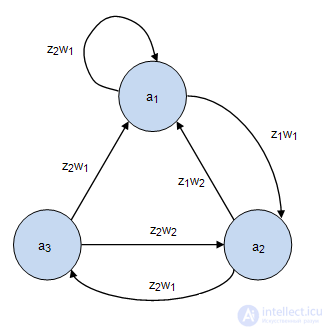
The input is the same input word:  . As a result, the output word is formed.
. As a result, the output word is formed.  which is the reaction of the automaton (Table 2.3).
which is the reaction of the automaton (Table 2.3).
| Moments of time | t1 | t2 | t3 | t4 | t5 | t6 | t7 |
|---|---|---|---|---|---|---|---|
| Input word | z1 | z1 | z2 | z1 | z2 | z2 | |
| States | a1 | a2 | a1 | a1 | a2 | a3 | a2 |
| Output word | w1 | w2 | w1 | w1 | w1 | w2 | |
| automatic reaction | |||||||
| Moments of time | t1 | t2 | t3 | t4 | t5 | t6 | t7 |
|---|---|---|---|---|---|---|---|
| Input word | z1 | z1 | z2 | z1 | z2 | z2 | |
| States | a1 | a4 | a2 | a1 | a4 | a3 | a5 |
| Output word | w1 | w1 | w2 | w1 | w1 | w1 | w2 |
| automatic reaction | |||||||
Two automatic  and
and 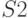 are called equivalent if:
are called equivalent if:
There is a theorem: for any Moore machine gun, there is an equivalent Mealy machine gun and vice versa.
In the tabular task, the transition table of the Mile automaton coincides with the transition table of the Moore automaton. The exit table of the Miles machine is obtained from the transition table by replacing the symbol 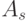 standing at the line crossing
standing at the line crossing 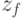 and column
and column 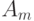 per character
per character 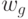 marking the column
marking the column 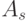 in the combined table of Moore’s machine gun.
in the combined table of Moore’s machine gun.
Let Moore's automaton be given (Table 2.4). The transition table of the equivalent Mile automaton (Table 2.5) coincides with the combined Moore automaton table representing the automaton transitions, and the output table 2.6 is obtained as follows. It is believed that on the transition from the state 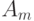 in state
in state 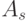 in the equivalent Miles machine, the same output signal should be generated as in the Moore machine, after the state machine went into
in the equivalent Miles machine, the same output signal should be generated as in the Moore machine, after the state machine went into 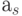 i.e. output signal
i.e. output signal 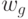 .
.
| w1 | w2 | w3 | w2 | w3 | |
|---|---|---|---|---|---|
| a1 | a2 | a3 | a4 | a5 | |
| z1 | a2 | a5 | a5 | a3 | a3 |
| z2 | a4 | a2 | a2 | a1 | a1 |
| a1 | a2 | a3 | a4 | a5 | |
|---|---|---|---|---|---|
| z1 | a2 | a5 | a5 | a3 | a3 |
| z2 | a4 | a2 | a2 | a1 | a1 |
| a1 | a2 | a3 | a4 | a5 | |
|---|---|---|---|---|---|
| z1 | w2 | w3 | w3 | w3 | w3 |
| z2 | w2 | w2 | w2 | w1 | w1 |
Consider the transition of the automaton from the state 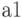 in state
in state 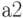 . In Moore's machine as
. In Moore's machine as 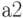 matches the output signal
matches the output signal 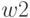 , therefore in table.2.6 at the transition from the state
, therefore in table.2.6 at the transition from the state 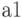 on input signal
on input signal 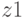 set
set 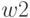 and so on.
and so on.
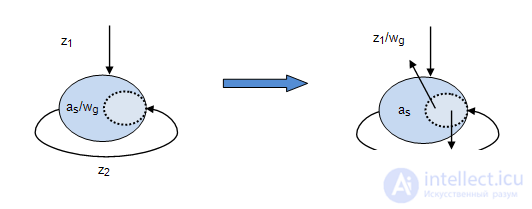
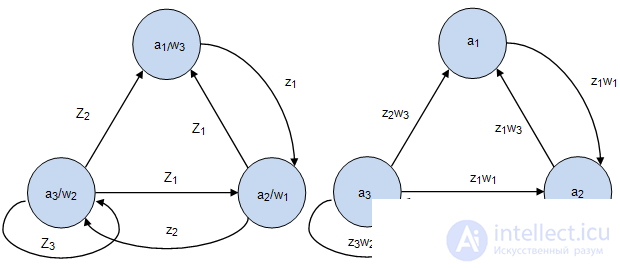
In the graphic task of Moore’s automaton, the transition to the Mile’s automaton is performed as follows: output signal 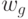 being molded into
being molded into 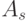 , is transferred to all the arcs entering this vertex, a graphical interpretation of this is shown in Figure 2.4, and an example of the transformation of the Moore machine gun into the equivalent Mealy machine is shown in Fig. 2.5.
, is transferred to all the arcs entering this vertex, a graphical interpretation of this is shown in Figure 2.4, and an example of the transformation of the Moore machine gun into the equivalent Mealy machine is shown in Fig. 2.5.
Restriction: In the Mile machine there should be no transition states, i.e. States in which there is at least one outgoing arc and there is not a single incoming arc, as shown in Fig. 2.6.
In Moore's automaton, the output signal 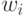 formed as a function
formed as a function 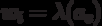 , and in the Miles machine -
, and in the Miles machine -  . And
. And 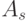 - the current state of the machine,
- the current state of the machine, 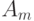 - the previous state of the machine. Thus, the state
- the previous state of the machine. Thus, the state 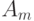 corresponds to a group
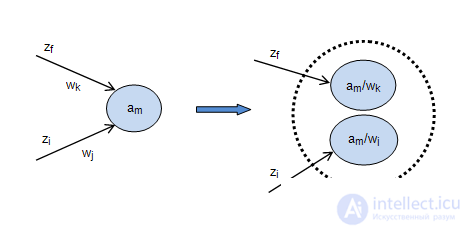
corresponds to a group  whose number is equal to the number of different output signals
whose number is equal to the number of different output signals  located on incoming arcs. A graphic interpretation of this is shown in Figure 2.7.
located on incoming arcs. A graphic interpretation of this is shown in Figure 2.7.
Let the Mile machine gun be given:  . I want to go to the equivalent Moore machine
. I want to go to the equivalent Moore machine 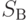 , that is, you need to build such an Moore automaton:
, that is, you need to build such an Moore automaton:  , what
, what  and
and  . Consider an example. Dan machine Miles Fig.2.8-2.9. We construct the set of states of the automaton.
. Consider an example. Dan machine Miles Fig.2.8-2.9. We construct the set of states of the automaton. 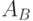 . For this we find the pair:
. For this we find the pair:
 ;
;
 ;
;
 ;
;
 .
.
Redesigning 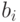 accordingly as
accordingly as 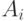 , we get the graph shown in Figure 2.8-2.9.
, we get the graph shown in Figure 2.8-2.9.
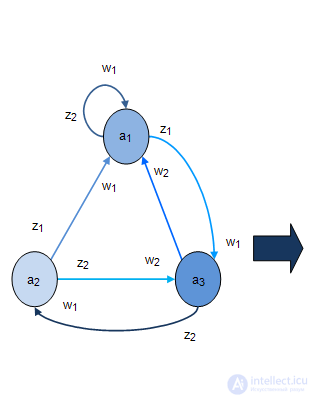 Fig. 2.8. | 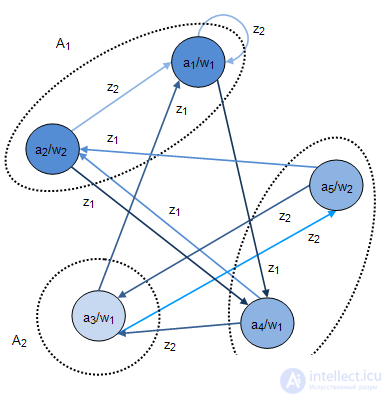 Fig. 2.8. |
Comments
To leave a comment
Theory of Automata
Terms: Theory of Automata