7: An example of the synthesis of a structural automaton on triggers

7.1 Synthesis of Moore's Structural Automaton on D Triggers

We briefly note the main stages of the synthesis of the automaton:

1. Find the number of memory elements (M is the number of states of the abstract automaton) and we encode the states of the abstract automaton.
2. Encode input and output signals.
3. The structural automaton is represented by a generalized scheme.
4. We compile a coded output table of the automaton and write the output equations using it.
5. We compile a coded automaton transition table and write equations for the excitation functions using it.
6. The equations of the excitation functions and outputs are minimized (using Carnot maps, for example) and a circuit is constructed from them in a given functional-logical basis of the basis ({AND, OR, NOT}, {AND-NO}, {OR-NOT}).

Let us consider the synthesis of the structural automaton Moore given by Table 7.1.1 on D-triggers in the elemental basis {AND, OR, NOT}.

1. Find the number of memory elements and encode the state of the abstract automaton, for example, as shown in Table 7.2.

   Table 7.2.

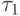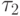   a 1	0	0
   a 2	0	one
   a 3	one	0
   a 4	one	one
2. We encode the input and output signals of an abstract automaton, for example, as shown in Table 7.3 and Table 7.4
3. The structural automaton is represented by a generalized scheme (Fig. 7.1).
   

   
   Fig. 7.1.

   Table 7.3.

   	X 1	X 2
   z 1	0	one
   z 2	one	0
   z 3	one	one

   Table 7.4.

   	r 1	r 2
   u 1	0	0
   u 2	0	one
   u 3	one	0
4. Table 7.1.1 is represented using state codes, input and output signals (Table 7.5), and using it we write the equations of the outputs.

   Table 7.5.

   r 1 r 2	00	01	ten	00
   x 1 x 2 \	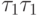00	01	ten	eleven
   01	00	ten	00	-
   ten	-	00	eleven	01
   eleven	eleven	01	ten	ten

   The output function r ₁ , which depends on Moore’s automaton only on the state, takes a single value on a single set of 10, i.e. 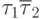. The output function r ₂ takes a single value also on a single set of 01, i.e. .

   Thus, the equations of outputs:

   ,

   .
5. Write the equations for the excitation functions. Since the excitation function in the D-trigger coincides with the transition state, the excitation function can be written from Table 7.5. We find single states of the first trigger. There are only five of them, see table 7.5. The excitation function depends on the input signals and the state of the machine from which this trigger was switched: .

   The first unit value of the excitation function takes upon transition from the state a ₀ , encoded as 00, i.e. , at receipt of single input signals . Similarly, we find the remaining terms and write the excitation function of the first trigger:

   

   For the second trigger of transition states in which it takes single values, four. They are highlighted in dark red. According to them recorded the excitation function of the second trigger:

   
6. Equations of excitation functions and outputs are minimized by Carnot maps (Fig.7.2).

Fig. 7.2.

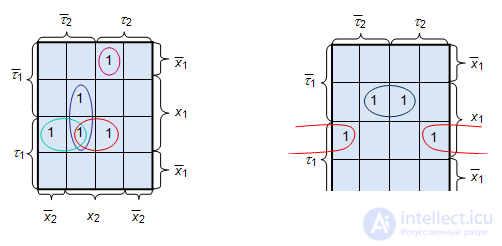
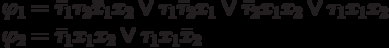
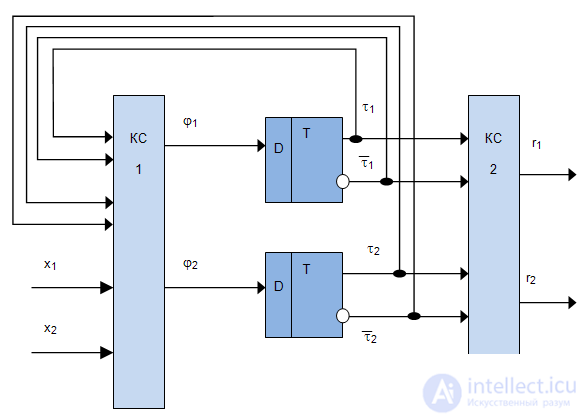
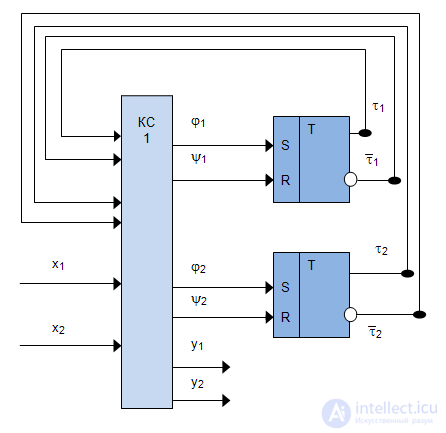
Using the obtained equations for the excitation functions and outputs, we construct a functional-logic circuit (Fig. 7.3).

Fig. 7.3.

7.2 Synthesis of Moore's structural automaton on T-triggers

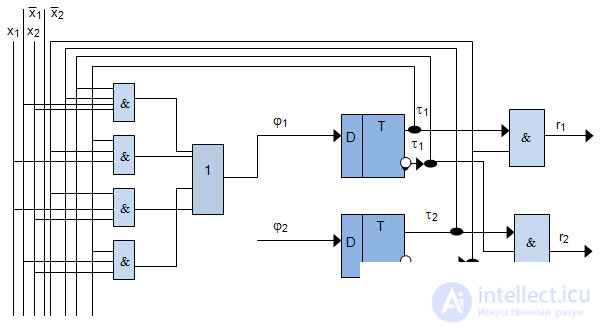
The stages of coding, the construction of a generalized scheme, the construction of equations of outputs coincide with the stages of synthesis on D-triggers. Consider the construction of the equations of excitation functions, that is, starting from the fifth stage.

Table 7.6.

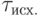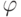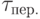0	0	0
0	one	one
one	one	0
one	0	one

Table 7.7.

r 1 r 2	00	01	ten	00
	00	01	ten	eleven
01	00	ten	00	-
ten	-	00	eleven	01
eleven	eleven	01	ten	ten

Table 7.8.

	00	01	ten	eleven
01	00	eleven	ten	-
ten	-	01	01	ten
eleven	eleven	00	00	01

Since the excitation function of the T-trigger (Table 7.6) 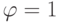, only when the state of the automaton goes from 0 to 1 or from 1 to 0, then using the encoded Fig.7.7 transitions of the original Moore's automaton, we find such trigger switches for which they change their states. We compile a table of excitation functions, which has state codes as column headings, and rows are labeled with input signal codes (Table 7.8). In each cell of the table recorded excitation function We make the equations for them:

Further, the equations are minimized and a scheme is constructed using them in a given basis.

7.3 Synthesis of the structural machine Miles on RS-triggers

Consider the synthesis of the structural Mile automaton given by Table 7.9 and Table 7.10 on RS triggers in the elemental basis {AND, OR, NOT}.

Table 7.9.

z \ a	a1	a2	a3	a4
z1	a1	a3	a1	-
z2	-	a1	a4	a2
z3	a4	a2	a3	a3

Table 7.10.

z \ a	a1	a2	a3	a4
z1	w1	w3	w1	-
z2	-	w1	w2	w2
z3	w2	w2	w3	w3

1. We find the number of memory elements R = 2 and encode the states of the abstract automaton, for example, as shown in Table 7.11.

   Table 7.11.

   	t 1	t 2
   a 1	0	0
   a 2	0	one
   a 3	one	0
   a 4	one	one
2. We encode the input and output signals of an abstract automaton, for example, as shown in Table 7.12 and Table 7.13.

   Table 7.12.

   	x 1	x 2
   z 1	0	one
   z 2	one	0
   z 3	one	one

   Table 7.13.

   	y 1	y 2
   w 1	0	0
   w 2	0	one
   w 3	one	0
3. The structural automaton is represented by a generalized scheme (Fig. 7.4).
   

   
   Fig. 7.4.
4. Table 7.10 is represented using state codes, input and output signals (Table 7.14), and using it we write the equations of the outputs.

   Table 7.14.

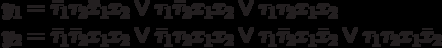
   x 1 x 2 \ t 1 t 2	00	01	ten	eleven
   01	00	ten	00	-
   ten	-	00	01	01
   eleven	01	01	ten	ten
5. We compile a coded automaton transition table (Table 7.15) and write equations for the excitation functions on it.

   Table 7.15.

   r 1 r 2	00	01	ten	00
   x 1 x 2 \ t 1 t 2	00	01	ten	eleven
   01	00	ten	00	-
   ten	-	00	eleven	01
   eleven	eleven	01	ten	ten

The excitation function of the RS-trigger is presented in table 7.16. Looking through each transition of triggers on the transition table of the machine (Table 7.15), we compose a table of excitation functions (Table 7.17), which has state codes as column headings, and rows are labeled with input signal codes. In each cell of the table, the excitation functions are written for the first trigger and for the second trigger . We make the equations for them:

Table 7.16.

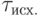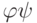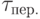0	0 -	0
0	ten	one
one	0 1	0
one	- 0	one

Table 7.17.

	0 0	0 1	ten	eleven
01	0- 0-	10 01	01 0-	-
ten	-	0- 01	-0 10	01 -0
eleven	10 10	0- -0	-0 0-	-0 01

Further, the equations are minimized and a scheme is constructed using them in a given basis.

Similarly, the synthesis is carried out on JK triggers.