The complexity of testing the structure of the PM

The complexity of the program is determined by the number of interacting components, the number of connections between the components and the complexity of their interaction. During the operation of the program, the diversity of its behavior and the diversity of connections between input and output data are largely determined by the set of routes along which the program is used. It was established that the complexity of the PM depends not only on the number of lines of the test, but also on the individual routes of use of the program. When creating a program, all possible data processing routes should be checked. This determines the complexity of the testing program.

Experimentally confirmed the adequacy of the use of the structural complexity of programs to assess the complexity of testing. The complexity of testing the PM can be estimated by the number of routes required for their testing or more fully by the total number of conditions that must be specified in the tests for passing all the routes of the program.
Ek =? Ei, where Mk is the number of routes required for the test, Ei is the number of conditions determining the i-th route
An example of evaluating the complexity of testing programs
An example of the initial graph of the module of the program. This graph contains 14 vertices, 20 arcs, 3 cycles and 7 predicate nodes. This program is not high complexity, which contains about 30-50 operators in a high level language. It can be considered as typical. For a complete check of this module by 1 criterion 4 routes are enough: 1-2-14; 1-3-4-6-8-6-8-14; 1-3-5-7-10-11-12-14; 1-3-4-5-7-9-10-9-10-11-7-9-10-11-12-13-14; Ek = 1 + 5 + 5 + 9 = 20

By this criterion, a check of all control transfers between the program operators and each operator is guaranteed for at least 1 time. The longest route does not cover only 3 vertices from 14 and 6 arcs from 20. After checking 2 more routes, 1 more vertex and 2 arcs remain out of control. However, the fulfillment of this criterion does not take into account the combinatorics of conditions on different sections of routes. For example, when combining the branch directions at vertices 3 and 12. The complexity of the program when allocating routes by this criterion is characterized by the number of routes = 4 and the complexity of testing = 2. This value characterizes the total number of conditions that must be specified in the tests for a complete check of all routes identified by criterion I. The condition at the vertices of each route can be used to autonomously generate predicates in the corresponding tests.

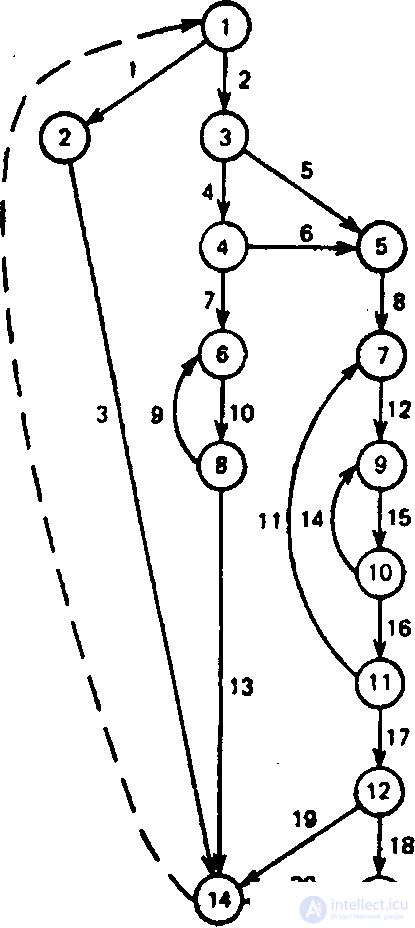
. Examples of assessing the complexity of testing programs

The second criterion for selecting routes in assessing the complexity of testing provides in the initial graph of the program a single test of each linearly independent cycle, which together form the basic routes. Each linearly independent route or cycle differs from all others by at least one vertex or arc. To determine the number of such routes, it is convenient to use the value of the cyclomatic complexity (CS) of the graph.
A CA is a software metric that provides a complete assessment of the logical complexity of a program. It determines the number of independent routes in the program and the upper estimate of the number of tests, which guarantees a single check of all operators. CA is calculated in 3 ways:
1. CA = number of closed areas of the graph
2. according to the formula CA = a-b + 2, a is the number of arcs, b is the number of nodes.
3. CA - the number of predicate nodes in the column +1
Routes by criterion II: 6-8, 9-10, 7-9-10-11, 1-2-14, 1-3-4-6-8-14, 1-3-5-7-9-10 -11-12-14, 1-3-4-5-7-9-10-11-12-14,1-3-4-5-7-9-10-11-11-12-13-14 .
The total complexity of the tests, taking into account all the conditions for the passage of routes, is equal to 25.
The most profound III criterion for checking and determining the complexity of testing the structure of a program includes the requirements of a single check for not only a set of independent, but also all linearly dependent cycles and acyclic routes. It consists in the analysis at least once of each of the real acyclic routes of the original graph of the program and of each cycle reachable from all these routes. For the graph of the program in the example according to the third criterion, 6 acyclic and 5 routes including elementary cycles must be performed. It is necessary to create 11 tests, they should contain 66 conditions. At the same time, the feature of 4 routes with cycles and the corresponding acyclic routes is a complete enumeration of combinations of branches 3 and 12 vertices. In real programs some. routes are not feasible due to incompatible conditions, cat. Consistently implemented in each vertex. For each route implemented, it may be necessary to check with several cycles and several values ​​of each variable to be processed. It is important to check the cycles with if output at 1-2 intermediate, as well as the max and min number of rounds of loop execution. As a result, the number of required tests and the duration of the test increases.
The complexity of testing acyclic PM
In engineering estimates of the number of routes in an acyclic PM, it is advisable to use the criterion of the cyclomatic number. To estimate the total complexity of the tests required for a complete check of acyclic PMs, you can use a value equal to the product of the number of routes and the number of vertices in the longest route / 2. The maximum complexity of tests according to criterion II for real acyclic programs is close to the number of branches in a square. Increasing the number of graph vertices by 4 times leads to an increase in the structural complexity of more than 10 times, therefore, to simplify the testing program, it is necessary to limit the size of the PM within 10-20 vertices.
The complexity of testing programs containing cycles
The presence of cycles in the program dramatically increases the complexity of its testing. Exhaustive testing should cover checking every route in a loop with all possible loop iterations and with all loop combinations with routes of the acyclic part of the program. Suppose for simplicity that the number of routes in the lower part of M3 = 1, then the full set of routes consists of the complete set of all routes M1 in the upper part of the program and the group of routes M2, which have several loop iterations attached to each route from M1.

In this case, at each iteration, at least 1 of the internal routes of the loop body is executed. For example, for a graph having 1 cycle, requiring execution of 5 turns with three internal routes and containing М1 = 10 acyclic routes passing through the cycle, the total number of routes for exhaustive testing = 5 * 3 * 10 = 150. As each factor increases, the complexity of testing, therefore, exhaustive testing of real complex programs is almost impossible.
The complexity of testing a cycle is influenced by its structure and 2 parameters: the number of routes in the body of the cycle and the number of iterations of the cycle. During the actual execution of the simplest cycle, there can be three types of dependencies between its iterations: 1) At various iterations of the cycle, various routes of the cycle body are used independently; 2) on all iterations of the loop, the same route of the loop body or some certain sequence of them is used; 3) at different iterations of the loop, due to the presence of semantic links, a subset of the implemented routes of the loop body is used, depending on the data or on the iteration number. The dependence of the 1st type is the most rare. In this case, there is a need for a complete enumeration of all internal routes of the loop body in combination with each number of iterations.
At the same time, the complexity of testing the cycle is determined by both parameters at once and approaches the complexity of exhaustive testing.
With dependence of 2 types the number of routes of the cycle body practically does not affect the complexity of the cycle. The number of iterations required to test the calculations in the body of the loop (for example, taking into account the required accuracy) becomes decisive.
The most common is 3 addiction. The decisive factor in evaluating the complexity of testing is not the number of loop iterations, but the number of loop body routes. The simplest estimates of the complexity of cyclic structures are advisable to move, assuming that the order of implementation of the routes of the loop body does not depend on the iteration number. In this case, when assessing the complexity of cyclic structures, the approach from the position min of the necessary number of checks of iterations of cycles is constructive.
To assess the complexity of the structural testing of logic programs with the simplest cycles, it is desirable to clarify the verification criteria. According to the 1st criterion, the acyclic part of the program is covered by a min number of routes, which includes routes passing through the cycle, opening it and forming the min covering of the cycle body. In addition, a route containing a closing arc of a loop is added to the coverage.

By criterion 2, the acyclic part of the program is checked by the number of tests equal to the complexity of the acyclic part. At the same time, all adjacent cycles join each such route. Verification of each cycle is carried out by one route, containing as many iterations as the complexity of the cycle body, and the cycle body is covered by linearly independent routes.
In such assessments, the determining factors are the completeness of checking the cycle body and the conditions of its closure / opening.
The variety of real cyclic structures in programs greatly complicates their analysis and obtaining generalized characteristics of the complexity and achievable test correctness.
When applying nested loops with a complex structure and with a large number of branches in the body of the loop, the complexity of testing dramatically increases the likelihood that undefined errors will be stored in the program.
Cycles with the simplest structure lead to a small increase in the total complexity of the tests, therefore, in the process of designing the program, it is necessary to simplify to the maximum extent the cyclic components in the structure.