Lecture
ax + b = 0. - Linear equation.
Solution of a linear equation: x = - b / a
Definition
A linear equation with one variable is an equation of the form ax = b, where a and b are numbers, x is a variable.
The root of a linear equation is the value of a variable, at which the equation becomes a true numerical equality.
For example, the root of the equation 5x = 40 is 8, since at x = 8, this equation turns into a true numerical equality:
5 ∙ 8 = 40
40 = 40.
The number of roots of a linear equation depends on the value of a (coefficient before x).
When a ≠ 0, the linear equation has a unique solution .
To find x, both sides of the equation must be divided by the number before X:
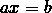
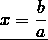
Any number can be divided by 2, 5 and numbers that can be represented as a product of only twos and fives (for example, any number can be divided by 10, since 10 = 2 5; by 40, because 40 = 2 2 ∙ 2 5).
In other cases, the answer is recorded in the form of an ordinary fraction (if the fraction is incorrect, one should extract the whole part from it).
When a = 0, b ≠ 0, the linear equation
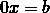
has no solutions .
For any value of x, the left side of the equation is zero, and the right side is non-zero. That is, there is not a single value of x at which the equation would turn into a true numerical equality.
When a = 0, b = 0, the linear equation
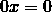
has an infinite number of solutions .
For any value of x, the left side of the equation 0x = 0 vanishes, and the right side also has zero. This means that any number is a root of this equation, that is, for any value of x, this equation becomes a true numerical equality.
Possible solutions of linear equations can be represented as a diagram.
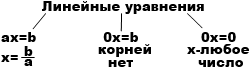
Solving a linear equation means finding the root (s) of the equation, or making sure that the equation has no roots.
The solution of many equations is reduced to the solution of linear equations.
Comments
To leave a comment
HANDBOOK ON MATHEMATICS, SCHOOL MATHEMATICS, HIGHER MATHEMATICS
Terms: HANDBOOK ON MATHEMATICS, SCHOOL MATHEMATICS, HIGHER MATHEMATICS