Types of algebraic equations a
n x
n + a
n-1 x
n-1 + ... + a
1 x + a
0 = 0. -
Algebraic equation of the n-th degree of general form. Let the coefficients a
k be real or complex numbers.
1. For brevity, we denote the left side of the equation, which is a polynomial of degree n, as follows:
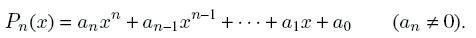
The number x = ξ is called the root of the equation, as well as the root of the polynomial P
n (x), if P
n ξ = 0. The number x = ξ is called the root of multiplicity m, if P
n (x) = (x = ξ)
m Q
nm (x), where m is a positive integer, 1 ≤ m ≤ m and Q
nm (x) is a polynomial of degree n - m, such that Q
nm (ξ) 0.
2.
The main theorem of algebra . The algebraic equation of nth degree has exactly n roots (real or cosplex), and the roots of multiplicity m occur exactly m times.
3. If an algebraic equation has roots x
1 , x
2 , ..., x
s , of multiplicities k
1 , k
2 , ..., k
s (k
1 + k
2 + ... + k
s = n), then the left side of the equation can be represented as:
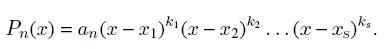
4. An algebraic equation of odd degree with real coefficients always has at least one real root.
5. Suppose an algebraic equation with real coefficients has a complex root ξ = α + iβ. Then this equation must also have a root η = α - iβ, and the multiplicities of both roots are the same. 6. The algebraic equation of degree n with integer coefficients a
k cannot have other rational roots than non-contractible fractions p / q, moreover p is the divisor of a
0 and q is the divisor of a
n . If a
n = 1, then all the rational roots of an algebraic equation are the integral divisors of the free a
0 and can be easily found.
7. Any equation of degree ≤ 4 is resolvable in radicals, which means that its roots can be expressed using the operations of addition, division, subtraction and multiplication, as well as extraction of the root. For n ≥ 4, algebraic equations, basically, in radicals are insoluble. This statement is called the Ruffini-Abel theorem.
8.
The Viet theorem . The following relations between the roots of an algebraic equation (taking into account their multiplicity) and their coefficients take place:
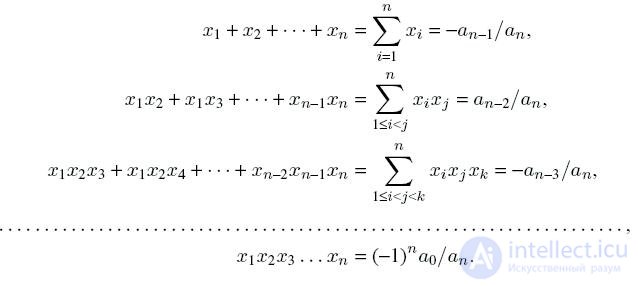
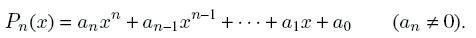
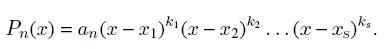
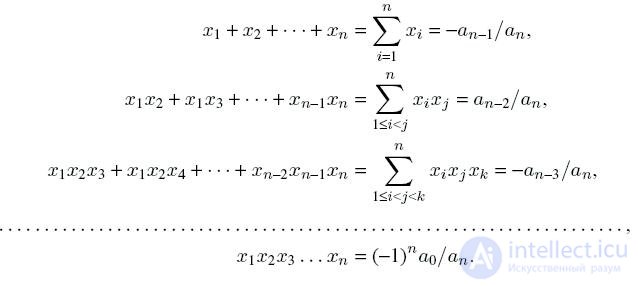
Comments
To leave a comment
HANDBOOK ON MATHEMATICS, SCHOOL MATHEMATICS, HIGHER MATHEMATICS
Terms: HANDBOOK ON MATHEMATICS, SCHOOL MATHEMATICS, HIGHER MATHEMATICS