ax
4 + bx
3 + cx
2 + dx + e = 0. -
Equation of fourth degree of general form. 1. Reduction to an incomplete equation The fourth degree equation is generally reduced to an incomplete equation.
y
4 + py
2 + qy + r = 0
by changing variables
x = y - b / 4a
2. Decarte-Euler Decision The roots of an incomplete fourth degree equation are determined by the formulas:
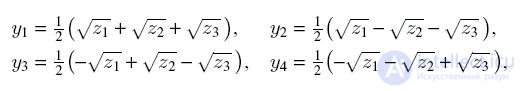
where z
1 , z
2 , z
3 are the roots of the cubic equation
z
3 + 2pz
2 + (p
2 - 4r) - q
2 = 0,
which is called the resolvent of the original equation. The signs of the roots in it are chosen in such a way that equality holds:
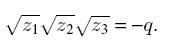
The roots of the incomplete initial equation are determined by the roots of the cubic resolvent according to the table:
The connection between the roots of an incomplete fourth-degree equation and the roots of the resolvent
| Cubic resolvent | Fourth degree equation |
| All roots are valid and positive (*) | Four valid roots |
| All roots are valid, they are positive and two are negative (*) | Two pairs of complex conjugate roots |
| One root is positive, two complex conjugates | Two real and two complex conjugate roots |
(*) - by the Viet theorem, the product of the roots z
1 , z
2 , z
3 = q
2 3. Ferrari Solution Suppose z
0 is one of the roots of an auxiliary cubic equation.
z
3 + 2pz
2 + (p
2 - 4r) - q
2 = 0,
Then the fourth roots of an incomplete fourth degree equation are found by solving two quadratic equations
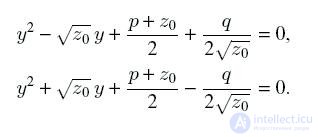
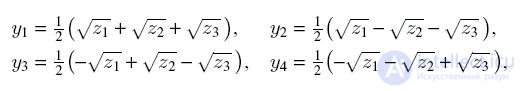
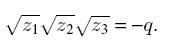
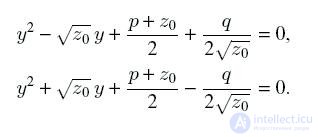
Comments
To leave a comment
HANDBOOK ON MATHEMATICS, SCHOOL MATHEMATICS, HIGHER MATHEMATICS
Terms: HANDBOOK ON MATHEMATICS, SCHOOL MATHEMATICS, HIGHER MATHEMATICS