Abbreviated Multiplication Formulas

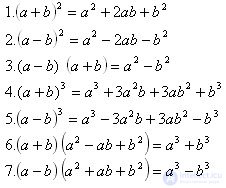
These formulas help solve problems faster and more accurately, especially when simplifying expressions or preparing for factorization.

History of abbreviated multiplication formulas

Abbreviated multiplication formulas have ancient roots and go back to deep antiquity, when mathematics was just forming as a science.

Ancient and classical times:
Babylon and India - more than 2000 years ago, mathematicians used primitive forms of these identities, especially the square of the sum and the difference of squares, when working with geometric problems and areas.

Euclid (c. 300 BC) — in his Elements, he describes geometric proofs of analogs of these formulas: for example, (a + b)² as the area of ​​a large square.

The Indian mathematician Brahmagupta (7th century) used algebraic identities to simplify calculations.

Middle Ages and Renaissance:
Arab mathematicians (Al-Khwarizmi and others) actively used formulas in developing algebra.

In Europe, thanks to the translation of Arabic texts into Latin, these formulas became part of university teaching in the 13th–14th centuries.

Modern times:
The formulas received a systematic form in the 17th–18th centuries, when algebra became a strictly formalized science.

Rene Descartes and Isaac Newton used them in analytical geometry and in the development of mathematical analysis.

Applications of abbreviated multiplication formulas

These formulas are widely used in many areas of mathematics and applied disciplines:

1. School and university mathematics
Simplification of expressions.

Solving equations.

Factorization of polynomials.

2. Algebra and mathematical analysis
Quick transformation of expressions in proofs.

Working with limits, derivatives and integrals.

3. Geometry and trigonometry
Calculations of lengths, areas and volumes.

Using areas in formulas, especially when working with squares and cubes.

4. Physics and engineering
Calculations of kinetic energy, moments of inertia and other physical quantities.

Simplification of formulas in process modeling.

5. Computer science
Symbolic computing algorithms.

Code optimization, especially in numerical methods.

6. Economics and statistics
Forecasting models.

Analysis of variation and dispersion (formulas of the type (a − b)² are found in dispersion calculation formulas).

6. Logic and development
development of logical and modular thinking.