ax
3 + bx
2 + cx + d = 0. -
Cubic equation.
Solution of the cubic equation:
1.
The decision of Cardano .
Roots of an incomplete cubic equation
y
3 + py + q = 0
expressed by the formulas:
Where
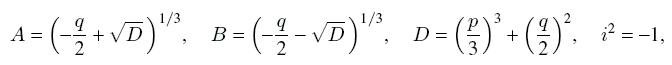
,
moreover, A and B are the values of the corresponding roots, for example AB = -p / 3.
The number of real roots of the cubic equation depends on the sign of the discriminant D:
D> 0 is one real root and two conjugate complex roots.
D <0 - three real roots.
D = 0 - one single real root and two double, or, if p = q = 0, then one triple real root.
2. Trigonometric solution
If the coefficients p and q of an
incomplete cubic equation are real, then its roots can be expressed in terms of trigonometric functions:
a) Let p <0 and D <0, then
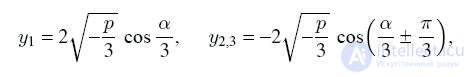
where the trigonometric functions are expressed as:
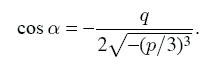
b) Let p> 0 and D ≥ 0, then
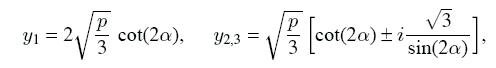
where trigonometric functions are expressed as:
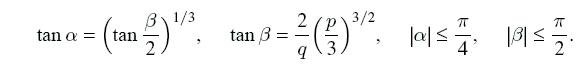
c) Let p <0 and D ≥ 0, then:
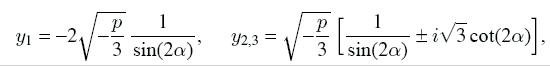
where trigonometric functions are expressed as:
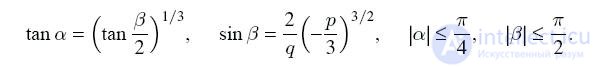
In all these cases, the actual values of the cube roots are taken.
3. The roots of the cubic equation ax
3 + bx
2 + cx + d = 0 are expressed by the formulas:
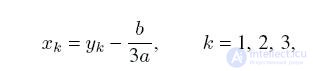
where y
k is the roots of an incomplete cubic equation with coefficients:
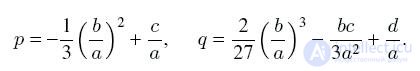 Vieta theorem
Vieta theorem for the roots of a complete cubic equation:
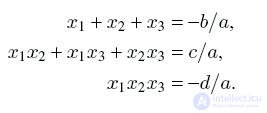
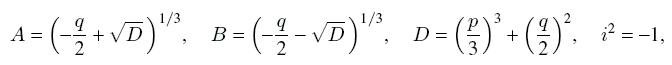 ,
,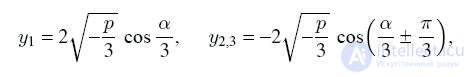
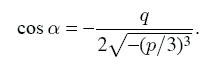
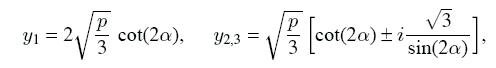
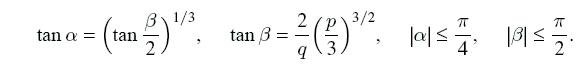
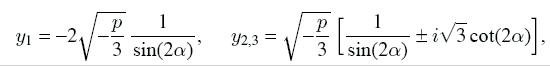
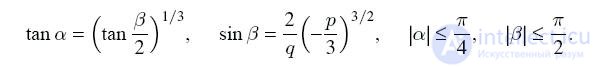
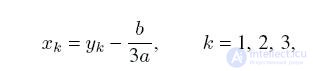
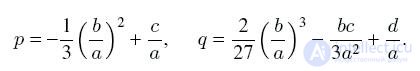
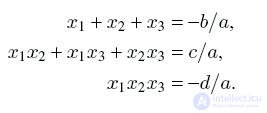
Comments
To leave a comment
HANDBOOK ON MATHEMATICS, SCHOOL MATHEMATICS, HIGHER MATHEMATICS
Terms: HANDBOOK ON MATHEMATICS, SCHOOL MATHEMATICS, HIGHER MATHEMATICS