Lecture
Это продолжение увлекательной статьи про имитация психологической интуиции с помощью искусственных нейронных сетей.
...
src="/th/25/blogs/id7106/541b4ddeb8934e798509517d14d92eff.png" data-auto-open loading="lazy" alt="Imitation of psychological intuition using artificial neural networks" > functions) in a situation where the density 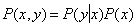 unknown, but random and independent sampling of pairs is given
unknown, but random and independent sampling of pairs is given 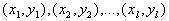 .
.
As it was shown in the previous paragraph of this chapter, the solution of the main problems of dependency recovery is achieved using the procedure of optimization of the quality functional.
Its solution will be considered in the approaches of the unconditional minimization of a smooth function. 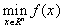 [77].
[77].
This task is directly related to the conditions for the existence of an extremum at the point:
- Necessary condition of the first order. Point 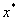 called the local minimum
called the local minimum 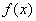 on
on 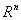 if there is
if there is 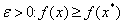 for
for 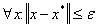 . According to the Fermat theorem if
. According to the Fermat theorem if 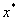 - minimum point
- minimum point 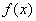 on
on 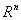 and
and 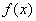 differentiable in
differentiable in 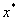 then
then 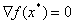
- A sufficient condition of the first order. If a 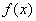 - convex function, differentiable at a point
- convex function, differentiable at a point 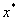 and
and 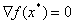 then
then 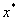 - global minimum point
- global minimum point 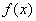 on
on 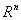
- Necessary condition of the second order. If a 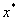 - minimum point
- minimum point 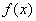 on
on 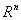 and
and 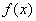 twice differentiable in it then
twice differentiable in it then 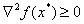
— Достаточное условие второго порядка. Если в точке 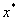
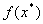 дважды дифференцируема, выполнено необходимое условие первого порядка (
дважды дифференцируема, выполнено необходимое условие первого порядка ( 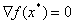 ) and
) and 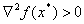 then
then 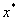 — точка локального минимума.
— точка локального минимума.
Условия экстремума являются основой, на которой строятся методы решения оптимизационных задач. В ряде случаев условия экстремума хотя и не дают возможности явного нахождения решения, но сообщают много информации об его свойствах.
Кроме того, доказательство условий экстремума или вид этих условий часто указывают путь построения методов оптимизации.
При обосновании методов приходится делать ряд предположений. Обычно при этом требуется, чтобы в точке 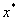 выполнялось достаточное условие экстремума. Таким образом, условия экстремума фигурируют в теоремах о сходимости методов.
выполнялось достаточное условие экстремума. Таким образом, условия экстремума фигурируют в теоремах о сходимости методов.
И, наконец, сами доказательства сходимости обычно строятся на том, что показывается, как «невязка» в условии экстремума стремится к нулю.
При решении оптимизационных задач существенны требования существования, единственности и устойчивости решения.
Существование точки минимума проверяется при помощи теоремы Вейерштрасса:
Let be 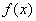 непрерывна на
непрерывна на 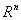 и множество
и множество 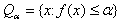 для некоторого
для некоторого 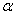 непусто и ограничено. Тогда существует точка глобального минимума
непусто и ограничено. Тогда существует точка глобального минимума 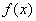 on
on 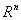
При анализе единственности точки экстремума применяются следующие рассуждения:
Точка минимума называется локально единственной, если в некоторой ее окрестности нет других локальных минимумов. Считается, что 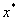 — невырожденная точка минимума, если в ней выполнено достаточное условие экстремума второго порядка (
— невырожденная точка минимума, если в ней выполнено достаточное условие экстремума второго порядка ( 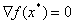 ,
, 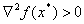 ).
).
Доказано, что точка минимума (строго) выпуклой функции (глобально) единственна.
Проблема устойчивости решения возникает в связи со следующим кругом вопросов:
—– 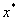 локального минимума
локального минимума 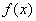 называется локально устойчивой, если к ней сходится любая локальная минимизирующая последовательность, то есть если найдется
называется локально устойчивой, если к ней сходится любая локальная минимизирующая последовательность, то есть если найдется 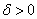 такое, что из
такое, что из 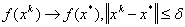 follows
follows 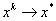
При обсуждении проблемы устойчивости решения задачи оптимизации можно выделить следующие важные теоремы.
— Точка локального минимума непрерывной функции 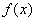 локально устойчива тогда и только тогда, когда она локально единственна.
локально устойчива тогда и только тогда, когда она локально единственна.
— Пусть 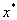 — локально устойчивая точка минимума непрерывной функции
— локально устойчивая точка минимума непрерывной функции 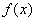 , but
, but 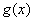 — непрерывная функция. Тогда для достаточно малых
— непрерывная функция. Тогда для достаточно малых 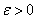 function
function 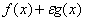 имеет локально единственную точку минимума
имеет локально единственную точку минимума 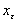 в окрестности
в окрестности 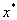 and
and 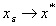 at
at 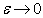
— Пусть 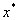 — невырожденная точка минимума
— невырожденная точка минимума 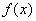 , а функция
, а функция 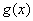 непрерывно дифференцируема в окрестности точки
непрерывно дифференцируема в окрестности точки 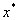 . Тогда для достаточно малых
. Тогда для достаточно малых 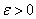 exists
exists 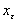 — локальная точка минимума функции
— локальная точка минимума функции 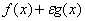 в окрестности
в окрестности 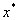 , and
, and 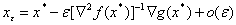
Помимо качественной характеристики точки минимума (устойчива она или нет) существенным является вопрос количественной оценки устойчивости. Такие оценки, позволяющие судить о близости точки 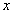 к решению
к решению 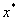 , if a
, if a 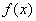 близко к
близко к 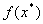 записываются следующим образом:
записываются следующим образом:
Для сильно выпуклых функций:
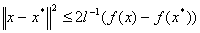
Where 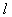 — константа сильной выпуклости.
— константа сильной выпуклости.
Для невырожденной точки минимума:
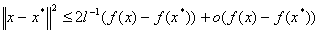
Where 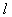 — наименьшее собственное значение матрицы
— наименьшее собственное значение матрицы 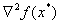 .
.
As you can see, in each of these definitions 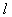 plays the role of characteristics of the "stability margin" of the minimum point.
plays the role of characteristics of the "stability margin" of the minimum point.
Besides 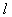 as the characteristics of the stability of the minimum point using the "normalized" indicator
as the characteristics of the stability of the minimum point using the "normalized" indicator 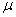 called the conditionality of the minimum point
called the conditionality of the minimum point 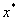 .
.

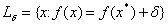
Can say that 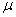 characterizes the degree of elongation level lines
characterizes the degree of elongation level lines 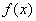 in the surrounding area
in the surrounding area 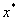 - “ravine” function (the more
- “ravine” function (the more 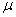 , the more "ravine" nature of the function).
, the more "ravine" nature of the function).
The most important ideologically the following methods of unconditional optimization: gradient and Newton.
The idea of the gradient method is to reach an extremum by iteratively repeating a procedure of successive approximations starting from the initial approximation. 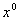 according to the formula
according to the formula 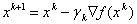 where
where 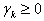 - step length.
- step length.
The convergence of this method is confirmed in the proof of the following theorem:
Let function 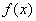 differentiable on
differentiable on 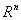 gradient
gradient 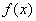 satisfies the Lipschitz condition:
satisfies the Lipschitz condition:
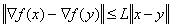 ,
,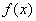 limited to below:
limited to below: 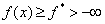
and 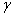 satisfies the condition
satisfies the condition 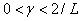
Then in the gradient method with a constant step 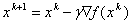 gradient tends to 0:
gradient tends to 0: 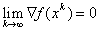 and function
and function 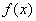 monotonously decreases:
monotonously decreases: 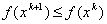
For strongly convex functions, stronger assertions on the convergence of the gradient method are proved.
When solving the optimization problem by the Newton method, an approach is used which consists in an iterative process of the form
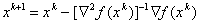
and in finding the extremum point as a solution of a system of n equations with n unknowns
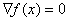 .
.In Newton's method, the equations are linearized at 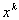 and solution of the linearized form system
and solution of the linearized form system
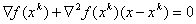
An analysis of the advantages and disadvantages of iterative optimization methods can be summarized in a table (see Table 3).
Table 3. Advantages and disadvantages of iterative optimization methods
| Method | Merits | disadvantages |
| Gradient | Global convergence, weak requirements for 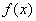 simplicity of calculations simplicity of calculations |
Slow convergence, the need to choose 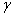 . . |
| Newton | Fast convergence | Local convergence, strict requirements for 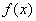 , a large amount of computation. , a large amount of computation. |
It can be seen that the advantages and disadvantages of these methods are mutually complementary, which makes it attractive to create modifications of these methods that combine the advantages of methods and are free from their disadvantages.
The modification of the gradient method is the method of the quickest descent:
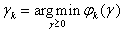 ,
, 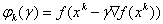
The modification of Newton's method in order to give it the property of global convergence is possible, for example, by adjusting the step length:
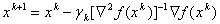
This method is called Newton's damped method. Possible approaches to the step selection method 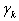 :
:
- Calculation by the formula
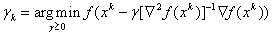 ;
;- Iterative algorithm, consisting in the sequential crushing step 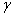 on constant
on constant 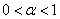 starting with
starting with 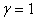 before the condition
before the condition
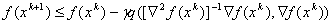 ,
, 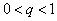
or conditions 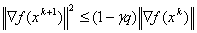 ,
, 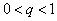
Newton's damped method converges globally for smooth strongly convex functions.
In addition to single-step methods, which include the gradient method and Newton's method, there is a whole class of multi-step methods that use information obtained from previous steps to optimize. These include:
- 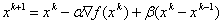 where
where 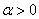 ,
, 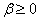 - some parameters. The introduction of inertia motion (member
- some parameters. The introduction of inertia motion (member 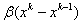 ) in some cases leads to acceleration of convergence due to the alignment of movement along the “gill-like” relief of the function;
) in some cases leads to acceleration of convergence due to the alignment of movement along the “gill-like” relief of the function;
- The conjugate gradient method. Here the optimization parameters are found from the solution of the two-dimensional optimization problem:
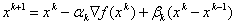 ,
,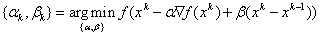
In addition to all the above optimization methods, there is also a class of methods based on the idea of restoring the quadratic approximation of a function from the values of its gradients at a number of points. These include:
- 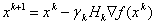 where matrix
where matrix 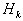 recalculated recursively based on information obtained on k- yiteration, so that
recalculated recursively based on information obtained on k- yiteration, so that 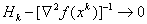 . Such methods include DFP (Davidon-Fletcher-Powell method) and BFGS or BFGSH (Broyden-Fletcher-Goldfarb-Shanno method) [46].
. Such methods include DFP (Davidon-Fletcher-Powell method) and BFGS or BFGSH (Broyden-Fletcher-Goldfarb-Shanno method) [46].
- 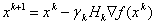 ,
, 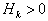 can be considered as gradient in metric
can be considered as gradient in metric 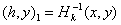 , and the optimal choice of metrics is
, and the optimal choice of metrics is 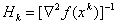 .
.
In this paper, the problem of pattern recognition and dependency recovery will be solved mainly using neural networks. The review of this topic is based on [1] - [6], [8] - [15], [22], [23], [32] - [34], [36] - [41], [59], [ 64], [67] - [70], [83] - [88].
The neural network is a structure of interconnected cellular automata, consisting of the following main elements:
A neuron is an element that converts an input signal by function:
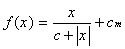
where x is the input signal, c is the parameter that determines the steepness of the graph of the threshold function, and c m is the parameter of spontaneous neuron activity.
Adder - an element that performs the summation of signals arriving at its input:
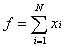
A synapse is an element that performs linear signal transmission:
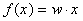
where w is the “weight” of the corresponding synapse.
The network consists of neurons connected by synapses through adders according to the following scheme:
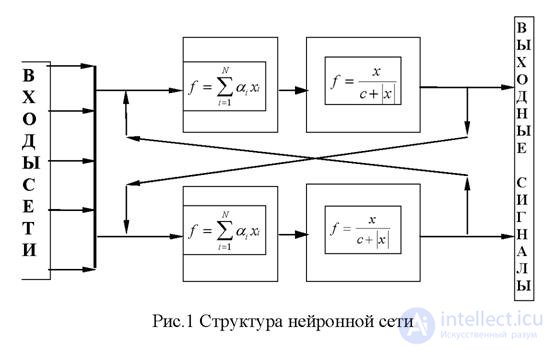
The network operates discretely in time (clock cycles). Then synapses can be divided into “communication synapses”, which transmit signals in a given clock cycle, and “memory synapses”, which transmit a signal from the output of a neuron to its input at the next clock cycle . The signals arising during the operation of the network are divided into direct (used when the network produces results) and dual (used in training) and can be given by the following formulas:
For the i-th neuron at the time step T:

where m i0 is the network initiation parameter, x i1 is the network input signals arriving at this neuron, f iT is the neuron output at the time step T, A i1 is the input parameter of the i-th neuron at the first network operation time, A iT is the input the signal of the i-th neuron at the time step T, a ji is the weight of the synapse from the j-th neuron to the i-th, a Mi is the weight of the synaptic memory of the i-th neuron, a i1 is the neuron parameter and a i2 is the parameter of spontaneous neuron activity, a iT-1 - input i-th neuron in cycle T-1, f jT-1 - the output signal j-th neuron in cycle T-1 and f iT, a - derivative i-th neuron to the input of its persecuted.
For a synapse connection from the i-th neuron to the j-th:

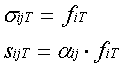
where s jT is the input signal of the synapse from the i-th neuron to the j-th, f iT is the output signal of the i-th neuron, a ij is the weight of the given synapse, s ijT is the output signal of the synapse at the time step T.
For the synapse memory i-th neuron: 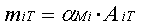
In this task, the training will take place according to the “connectionist” model, that is, by adjusting the weights of the synapses.
The essence of learning is to minimize the error function. 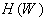 where W is the synaptic weights map. To solve the minimization problem, it is necessary to calculate the gradient of the function using adjustable parameters:
where W is the synaptic weights map. To solve the minimization problem, it is necessary to calculate the gradient of the function using adjustable parameters:
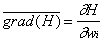
The gradient is calculated during the countdown of time ticks 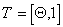 according to the following formulas:
according to the following formulas:
For synapse communication:
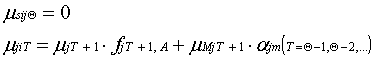
For memory synapse:
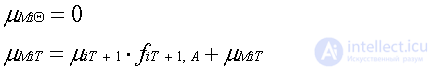
Finally, after passing the q clock ticks, the partial derivatives on the weights of synapses will have the form for synapses of memory and for synapses of communication, respectively:

1. The mathematical apparatus used in psychodiagnostics does not sufficiently meet modern requirements.
2. A pressing need is the introduction of the mathematical apparatus associated with pattern recognition and dependency recovery into psychodiagnostic techniques.
3. The existing mathematical methods and algorithms are too complex and time-consuming for their use by subject specialists, including psychodiagnostics, and do not allow computer techniques to follow the experience of a human specialist directly from precedents.
4. The use of the mathematical apparatus of neural networks when creating neural network expert psychological systems allows minimizing the requirements for the mathematical preparation of their creators.
The specific features of the mathematical apparatus of neural networks, described in detail in [36], [41] and the experience of their application in various fields of knowledge (see, for example, [5], [8], [10], [13], [84], [ 86]) suggested the possibility of solving psychological problems with their help.
It was supposed to test several possibilities of using neural networks, namely:
- Firstly, it was expected to solve a serious problem arising from the developers and users of computer psychological tests, namely the adaptability of methods. The mathematical construction of modern objective diagnostic tests is based on a comparison, comparison of the identified condition with the norm, the standard [21], [71]. However, it is clear that the norms worked out for one sociocultural group are not necessarily the same for another (for example, the difficulties that have to be overcome when adapting foreign methods can be cited). Neural network simulators have a useful feature in this case to train on the material provided by a particular researcher.
- Secondly - it was supposed to use a neural network simulator as a working tool of the researcher.
- Thirdly, the assessment of the possibility of creating new, non-standard test methods using neural networks. It was supposed to check the possibility of issuing direct recommendations on the transformation of the real state of the object, bypassing the stage of setting the diagnosis (building “measured individuality” [26]).
The study was performed using neural network software simulators of the NeuroComp association [36], [41], [70], [85], [87] using psychological material collected at the Krasnoyarsk Garrison Military Hospital.
First of all, it was necessary to find out whether the level of diagnostics that has already been achieved using standard psychological tests is available to the neural networks. In order to obtain the results of maximum reliability, the psychological method LOBI [57] (Personal Questionnaire of the Bekhterevsky Institute) that was sufficiently tested by clinical practice was chosen. In addition, an important factor in choosing this particular test was the fact that the technique is clearly algorithmized and has a realization in the form of a computer test.
So, the task of the experiment was to determine how adequately a neural network simulator can reproduce the results of a typical psychological methodology in diagnosing a patient.
Having considered this problem, as well as the available neural network programs, it was decided to use the MultiNeuron neural network simulator (for a description of the package, see [85], [87]).
The MultiNeuron software package is a neurocomputer simulator implemented on the IBM PC / AT, and, among other functions, is designed to solve n-ary classification problems. This software package allows you to create and train a neural network in order to determine by the set of input signals (for example, by answering asked questions) that an object belongs to one of n (n <9) classes, which will be further numbered with integers from 1 to n. Необходимая для обучения выборка была составлена из результатов обследования по методике ЛОБИ 203 призывников и военнослужащих проходящих лечение в Красноярском гарнизонном военном госпитале и его сотрудников. При этом было получено 12 файлов задачника для MultiNeuron (по гармоническому типу выборка содержала недостаточно данных — 1 пример с наличием данного типа).
The taskbooks were formed from response lines, which are a chain of 162 signals, each of which was responsible for 1 of the LOBI questionnaire questions according to the following principle: -1 - a negative answer to this question was selected, 1 - a positive answer was selected, 0 - no question was selected. This notation was chosen based on the desirability of normalizing the input signals supplied to the input of neurons in the interval [-1,1]. The answer was set by classes, class 1 - the type is missing, class 2 - the type is diagnosed. At the same time, for the purity of the experiment according to the types of stress response itself, it was decided to abandon the diagnosis of a negative attitude towards the study and exclude such examples from the training set.
In general terms, the essence of the experiments was as follows: some examples of the original sample were randomly excluded from the learning process. After that, the neural network was trained on the remaining ones, and the selected examples made up a test sample on which it was checked how the calculated answers of the neural network correspond to the true ones.
In the process of learning neural networks with different characteristics, the author came to the conclusion that for this task it is possible to limit the number of neurons to 2 (that is, 1 neuron for each of the classes). The best results when testing on a test sample showed networks with a characteristic number of neurons c = 0.4.
For detailed processing, a sample was taken that is responsible for the ergopathic type LOBI. A series of network training experiments showed that a fully connected network trained on a sample of 152 examples does not show a better result than 90% of correct answers (on average, about 75%). The same result was confirmed during the end-to-end testing, when training was performed on 202 examples, and tested 1. After training 203 networks, a similar result was obtained by this method - 176 examples were confidently correctly identified (86.7%), uncertainly correctly - 4 (1.97% ), incorrect - 28 (13.79%), that is, the total percentage of correct answers was 88.67. It should be noted, however, that an increase in the number of examples of a training sample of up to 200 made it possible to improve the number of correct answers to a guaranteed value of 88.67% (see above). It should be assumed that a further increase in the training sample will allow us to further improve this result. In addition, the cause of errors in determining the ergopathic type by LOBI may be hiding in an insufficient number of examples with the presence of this type (the ratio of examples with the presence and absence of the type is 29: 174). This is also confirmed by the fact that among the examples with the presence of the type, the percentage of incorrect answers (12 out of 29 or 41.38%) is incomparably higher than in the sample as a whole. Thus, it can be concluded that neural networks, using certain methods of improving results (see below), allow us to create computer psychological tests that are not inferior to the currently used methods, but have a new and very important in practice property - adaptability.
Also of interest is the result obtained when assessing the significance of input signals (respectively, LOBI questions).
Let some functional element of the neural network transform the vector of signals A arriving at it according to some law 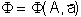 where
where 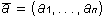 - vector of adaptive parameters. Let H be the evaluation function, which depends explicitly on the output signals of the neural network and implicitly on the input signals and parameters of the neural network. In dual operation, partial derivatives will be calculated.
- vector of adaptive parameters. Let H be the evaluation function, which depends explicitly on the output signals of the neural network and implicitly on the input signals and parameters of the neural network. In dual operation, partial derivatives will be calculated. 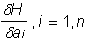 for the element v. These derivatives show the sensitivity of the estimate to the parameter change.
for the element v. These derivatives show the sensitivity of the estimate to the parameter change.  the more
the more 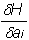 , the more H changes when this parameter is changed for this example. It may also turn out that the derivative with respect to some parameter is very small compared to the others, which means that the parameter practically does not change during training. Thus, it is possible to single out a group of parameters, to changes of which the neural network is the least sensitive, and in the process of learning they do not change at all. Of course, to determine the group of the smallest or greatest sensitivity, it is necessary to use partial derivatives of the evaluation function by parameters in several training cycles and for all examples of the problem book. During neural network learning, the dynamics of the decrease in the evaluation function changes at different stages of learning. It can be important to determine which inputs at this stage of learning are essential for a neural network, and which are not. Such information is useful in cases where the dimension of
, the more H changes when this parameter is changed for this example. It may also turn out that the derivative with respect to some parameter is very small compared to the others, which means that the parameter practically does not change during training. Thus, it is possible to single out a group of parameters, to changes of which the neural network is the least sensitive, and in the process of learning they do not change at all. Of course, to determine the group of the smallest or greatest sensitivity, it is necessary to use partial derivatives of the evaluation function by parameters in several training cycles and for all examples of the problem book. During neural network learning, the dynamics of the decrease in the evaluation function changes at different stages of learning. It can be important to determine which inputs at this stage of learning are essential for a neural network, and which are not. Such information is useful in cases where the dimension of
продолжение следует...
Часть 1 Imitation of psychological intuition using artificial neural networks
Часть 2 1.7 Neural networks - Imitation of psychological intuition using artificial
Часть 3 Chapter 3. Intuitive Neural Network Prediction of Relationships - Imitation
Часть 4 LITERATURE - Imitation of psychological intuition using artificial neural networks
Comments
To leave a comment
Mathematical Methods in Psychology
Terms: Mathematical Methods in Psychology